3. Методы решения нелинейных сау

3.1. Постановка задачи

Во введении было сказано, что при определенных условиях ЭО в установившемся режиме описывается системой нелинейных АУ вида (1.2). Если при этом входной сигнал известен, то для опре­деления соответствующего значения необходимо решить систе­му нелинейных АУ вида

F(x)=0 (3.1)

Точно решить систему (3.1) удается редко, поэтому решение находим в два этапа:

- определение приближенного значения;

- уточнение приближенного значения с помощью некоторого итераци­онного метода до некоторой заданной степени точности.

Часто значение известно из каких либо практических сооб­ражений, связанных со знанием ЭО. Для малых n значения вектора можно определить графически. Если метод решения обладает глобаль­ной сходимостью, то может быть любым. Мы сосредоточим свое внимание на втором этапе.

Численный метод, в котором производится последовательное, шаг за шагом, уточнение первоначального грубого приближения называется итерационным. Шаг в этом методе называется итерацией. Если с каждым шагом получаемое значение x все ближе к точному то метод сходится .

Обобщенный алгоритм решения нелинейных систем АУ. Большинство известных итерационных методов решения системы (3.1) можно за­писать одной общей формулой

(3.2)

где G - вектор-функция размерности n , которая определяется спо­собом построения итерационного процесса; р - количество предыдущих значений x , используемых в данном итерационном процессе.

Если в итерационном процессе используется только одна предыду­щая точка (p=1), то

(3.3)

В дальнейшем мы будем обсуждать только эти методы.

Основные характеристики итерационных методов:

I. Сходимость итераций. Итерации сходятся, если

. (3.4) (3.4)

Вектор-Функция G(x) называется изображением итерационного про­цесса. Спектральным радиусом квадратной матрицы называ­ется максимальный из модулей ее собственных значений. Предположим, что функция G(x) определена и непрерывна вместе со своей первой производной

Теорема сходимости. Если спектралъный радиус матрицы и если векторы не выходят за области оп­ределения вектор-функций F и G , то процесс итераций (3.3) сходится. При этом предельный вектор является един­ственной точкой притяжений итераций[3].

Эта теорема справедлива для .любого начального приближения и поэтому относится к теоремам о глобальной сходимости. Условие теоремы можно записать и непосредственно через собственные числа матрицы

(3.5)

Очевидно, что эти условия согласуются с требованиями асимптоти­ческой устойчивости дискретных динамических систем вида (1.9). Действительно, линеаризованная система (3.3)

является обычной дискретной системой и требования ее асимптоти­ческой устойчивости сводятся к неравенству (3.5), которое должно выполняться при любом m .

Так как то условие (3.5) можно переписать в виде

,

где - норма матрицы .

Известно, что последнее неравенство будет выполнено, если соблю­дены неравенства

, (3.6)

или

Очевидно, что первая груша неравенств - сумма модулей элементов матрицы по строкам, а вторая - по столбцам. Однако упомянутые соотношения являются достаточными условиями сходимости, но не необходимыми, так как в сравнении, с неравенством (3.5) предъявляют к матрице завышенные требования.

Трудность применения теоремы о глобальной сходимости состо­ит в том, что надо определять величины , на каждом m -м шаге итерационного процесса. Это практически невозможно. Поэтому нашли применение теоремы локальной сходимости . При этом предполагают, что точка ' лежит близко к . Спектральный ра­диус матрицы вычисляется только в точке .

2)Выбор величины зависит от вида сходимости метода. Если метод имеет локальную сходимость, то должно быть Слизко к , если глобальную, то - любой. Часто .

3)Скорость сходимости итераций оценивается по скорости уменьшения величины ошибки

,

если условия сходимости выполняются, то часто скорость можно оценить формулой

где k-целое число; c -константа.

Если k=1 , то итерационный метод имеет линейную сходимость. При этом, если с 1 , то сходимость медленная (метод простой итерации) .

Если k=2 то метод обладает квадратичной скоростью сходимости. Так как то будет величиной второго по­рядка малости и поэтому скорость велика (метод Ньютона).

4) Критерий окончания итераций. Расчеты по формуле (3.3) не могут длиться бесконечно долго. Очевидно, что критерием окончания итерационного процесса могла бы служить величина но нам неизвестно значение . В связи с этим величину можно оценить косвенно.

Способ 1. Остановить процесс вычислений, когда заданной допустимой погрешности. Заметим, что .

Способ 2. Остановить процесс вычислений, когда ,

Чем ближе к , тем меньше величина .

Выбор способа зависит от характера поведения функций вблизи решения. Рассмотрим два рисунка: рис.3.1 и 3.2

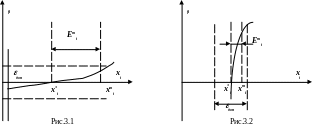
Из рис.3.1 видно , что если заканчивать итерационный процесс по величине , то при этом можно оказаться довольно далеко от по .На рис. 3.2 - наоборот, итерационный процесс закан­чивается при малых значениях , что приводит к большим ошибкам по .

Способ 3. Чтобы избежать недостатков первых двух способов, контролируют обе нормы, а итерационный процесс заканчивают при том значении m , при котором

. (3.7)

Следует заметить, что при плохой обусловленности матрицы вблизи возможны колебания значений норм. Тогда нужно применять специальные методы уменьшения этих колебаний (здесь не рассматри­ваются).

Ввиду небольшого объема пособия, ограничимся рассмотрением тех методов, которые являются наиболее эффективными при решении практических задач. К ним относятся метод Ньютона и два других, являющихся развитием метода Ньютона.