2.2. Явный метод Эйлера и его характеристики

Алгоритм определяется формулой (2.7). Для дальнейшего анализа рассмотрим интегрируемую систему . линеаризовав ее предварительно в точке

(2.8)

Способ вычисления элементов матрицы A описан выше в соот­ветствующем разделе. Мы обратим внимание лишь на то, что входной сигнал при линеаризации является известной функцией времени и при фиксированном на шаге может считаться константой. Ввиду того, что для линейной системы, как уже упоминалось ранее, свойство устойчивости зависит лишь от А , то входной сигнал в системе (2.8) не показан. Кроме того, очевидно, что элементы матрицы А меняются с изменением точки линеаризации, т.е. с изменением m.

В связи о этим введем понятие локальных собственных чисел матри­цы А , которые постоянны на данном шаге, но меняются от шага к шагу. Чтобы не загромождать формулу множеством обозначений, ин­декс m при матрице А и ее собственных числах опустим.

Рассмотрим характеристики метода.

1) Точность метода. Ранее уже было показано, что формула ин­тегрирования (2.7) аппроксимирует ряд Тейлора для функции до линейного по h члена включительно. Поэтому пропорцио­нальна . Можно показать, что существует такое значение в интервале при котором

2) Устойчивость. Для анализа устойчивости приведем матрицу А к диагональной форме: . Тогда система (2.8) при­мет вид

Обозначив , перейдем к новым переменным:

(2.9)

Так как матрица , то система (2.9) распадает­ся на n независящих друг от друга дифференциальных уравнений . В дальнейшем индекс i опустим, потому что он не имеет принципиального значения:

(2.10)

Метод Эйлера для уравнения (2.10) будет иметь вид

(2.11)

Здесь опущен индекс m при h для простоты записи, однако надо помнить, что величина меняется от шага к шагу.

Выясним, как численная устойчивость зависит от . Характе­ристическое уравнение для дискретной системы (2.11) будет иметь вид

В дальнейшем корни характеристического уравнения дискретной систе­мы будем обозначать чтобы не путать их с . Здесь корень один

Случай 1. Нулевое состояние равновесия системы (2.10) асимп­тотически устойчиво, т.е . Следовательно, система (2.11) также должна обладать этим свойством, т.е. имеет место случай абсолютной устойчивости. метода интегрирования (2.11). Это значит, что корень по модулю должен быть меньше 1 (см. разд. "Устой­чивость дискретных систем):

или ( (2.12)

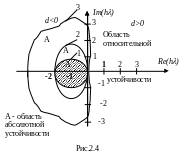
Областью абсолютной устойчивости, как следует из неравенства (2.12), будет круг радиусом, равным 1 и центром в точке. (0, -1) (рис.2.4 кривая 1). Таким образом, шаг h должен на каждом интервале интегрирования подбираться таким об­разом, чтобы при этом не покидать область А. Если корень - чисто вещественный, т.е. , то можно получить более удобную, чем соотношение (2.12), форуму условий абсолютной устойчивости. Действительно, если то из (2.12)

получаем

откуда приходим к следующему требованию:

где - постоянная времени системы (2.10). Она определяет скорость затухания переходных процессов в ней. Это нетрудно дока­зать, если учесть, что решение системы (2.10) имеет вид

Переходный процесс в этой системе затухает при . Обычно считают, что он закончен, если Подставив последнее выражение вместо в предыдущее, получим

,

откуда будем иметь, что время переходного процесса где

Если иметь в виду, что уравнений вида (2.10) n штук, то

(2.14)

где

Случай 2. Нулевое состояние равновесия системы (2.10) неус­тойчиво, т.е. .Следовательно, система (2.11) должна быть также неустойчива, т.е . Но, как уже упоминалось ранее, скорости изменения точного и приближенного решений уравнения (2 .10) должны быть близки. Это значит, что величина должна быть ограничена сверху. Какой величиной? Для ответа на этот воп­рос сравним точное и

приближенное решения уравнения (2.10). Для этого определим значение точного решения y(t) в точке Из сравнения этого выражения с выражением для следует

требо­вание или .

Нетрудно видеть что оно соблюдается для всех . Поэтому область устойчивости явного метода Эйлера является вся правая полуплоскость (рис.2.4).

3.Выбор шага интегрирования

Прежде всего должны соблюдаться условия абсолютной (2.12), (2.13) или относительной устойчивости (2.15) в зависимости от ха­рактера интегрируемой системы (2.1). Здесь необходимо сделать ряд замечаний:

- условие (2.13) для произвольного h примет вид , поэтому окончательно шаг по условиям устойчивости выби­рают

(2.16)

- условие (2.15) не дает способа выбора шага из соображений устойчивости, так как удовлетворяется при любых h.;

- в обоих случаях следует шаг корректировать по условиям точности:

- нужно помнить, что теоретически условия (2.15) и (2.16) должны соблюдаться на каждом шаге m . Очевидно, что их проверка на каждом шаге практически невозможна. Поэтому, например, условие (2.16) достаточно проверить при начальных значениях t и x , т.е. при m=0 , Далее шаг может корректироваться из условий точности.

Практические рекомендации по выбору шага состоят в следующем. Вна­чале задается допустимая ошибка . аппроксимации, например, не более от , т.е.

,

Если неизвестно, то можно взять - начальный момент времени. В процессе интегрирования шаг подбирает­ся так:

1) по формуле (2,7) определяется очередное значение

2) определяется да ,

3)условия соблюдения точности имеют вид ,

С другой стороны, исходя из формулы Эйлера (2.7),

,C

Тогда шаг должен удовлетворять условию:

,

Однако из последней формулы следует, что при малых значениях - шаг неограниченно растет и может выйти за пределы области ус­тойчивости метода. Пусть - максимально допустимый шаг, тог­да условие выбора шага с учетом ограничения его сверху будет иметь вид:

(2.17)

4) окончательно шаг на m-м интервале времени выбираем в виде:

Вопрос; как задать ? Это можно сделать, например из усло­вия устойчивости, рассчитывая по начальным условиям .