1.4. Критерий устойчивости дискретных систем

Систему (1.1) или (1.6) часто называют непрерывной, так как время в ней меняется непрерывно. Однако при реализации численных методов, на ЭВМ время дискретно и любой численный метод приводит нас к дискретной (или разностной) системе уравнений. В дальнейшем ми еще встретимся c большим количеством таких систем, но здесь рассмотрим один простой пример. Заменим в системе (1.5) производ­ную c помощью конечных разностей

Тогда, подставив последнее соотношение вместо в левую часть системы (1.5), получим после простых преобразований

Или введя обозначения: , ,

Это дискретная (или ревностная) система уравнений. Такая модель также относится к классу динамических и позволяет построить процесс x(t) во времени, правда дискретном, с шагом (рис 1.5).

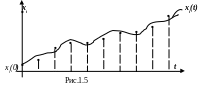
Утверждение. 1.2. Нулевое состояние равновесия системы (1.9)

асимптотически устойчиво тогда и только тогда, когда все . Если среди есть хотя бы один такой, что то нулевое состояние равновесия находится на границе устойчивости. Если среди

, найдется хотя бы один та­кой, что . то нулевое состояние равновесия неустойчиво.

Доказательство.

Пусть m - номер временного отсчета, тогда - номер на­чального момента времени. В этом случае система (1,9) перепишется в виде

При u(m) =0 решение имеет вид

Приведем матрицу к диагональному виду и тогда получим

Очевидно, что

Так как , то

В каком случае все составляющие будут уменьшаться при ? Если . Если хотя бы один корень , то система будет находиться на границе устойчивости так как в решении есть константа. Если

Хотя бы один корень то эта составляющая будет расти при и система станет неустойчивой. Утверждение доказано.

В заключение заметим , что при выводе всех условий численной устойчивости методов интегрирования систем ОДУ

или сходимости численных методов решения систем АУ опираются на утверждение 1.2.

2. Методы численного интегрирования систем оду

2.1 Постановка задачи

Пусть в системе ОДУ (1.1) входной сигнал u(t) известен. Тогда можно явную зависимость функции F от u не показывать , а записать систему (1.1) в более простом виде:

, (2.1)

где явная зависимость F от t включает в себя наличие входного сигнала u(t).

Численное интегрирование системы (2.1) заключается в опреде­лении значений x(t) на интервале времени от 0 до Т при заданных начальных условиях x (0) (для простоты начальный момент времени принят нулевым) (рис.2.1). При этом интервал времени от 0 до Т разбивается на шаги о интервалом здесь m- номер шага . Очередное значение вычисляетcя на основе предыдущих значений x . Поэтому в общем случае любой численный алгоритм интегрирования системы (2.1) может быть представлен в виде:

, (2.2)

где G - некоторая функция, определяемая конкретным методом;p-количество используемых предыдущих точек.

Если p = 1 , то метод одношаговый, иначе - многошаговый.

Одна из основных идей при построении (2.2) состоит в приме­нении к уравнению (2.1) формулы Ньютона-Лейбница

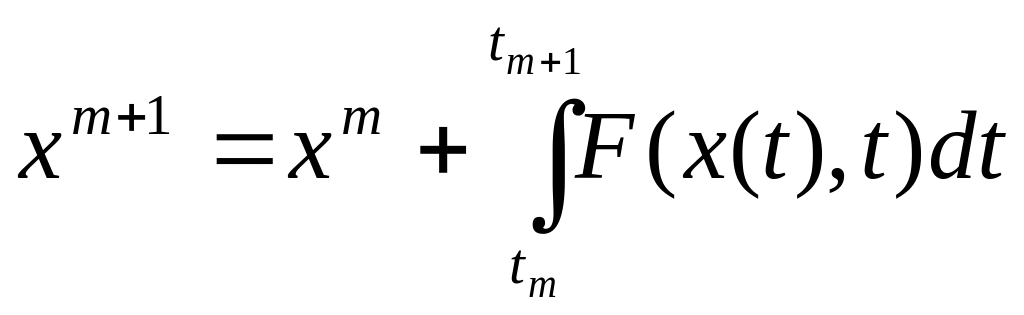
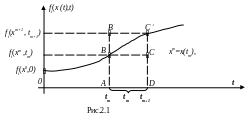
с последующей аппроксимацией интеграла. На рис.2.1 показан случай когда на интервале функция F(.), т.е. .значение считается постоянной. Если при этом упомянутая константа равна то получаем известное правило правых прямоуголь­ников:

здесь - ошибка замены точного значения ин­теграла в формуле- (2.3) его приближенным значением (площадью пря­моугольника АВСД).

Если считать, что производная , т. е. функция F(.) на ин­тервале равна то получаем правило левых прямоугольников (АБСД)

С точностью до ошибок аппроксимации и формулы (2.4) и (2.5) представляют собой явный и неявный соответственно методы Эйлера численного интегрирования системы ОДУ (2.1), В не­явном методе Эйлера для определения надо решать нелинейную систему АУ на каждом шаге. Используемые при этом численные методы будут рассмотрены ниже. Здесь заметим следующее: точки и достаточно близки друг к другу при малом . Поэтому можно брать в качестве начального приближения при решении системы АУ каким-либо итерационным методом и при этом обоснованно надеять­ся на то, что метод сойдется (например метод Ньютона).

Требования, предъявляемые к численным методам решения систем ОДУ вида (2.1):

1)универсальность, т.е. возможность применить данный метод к ана­лизу любой системы ОДУ, принадлежащей определенному классу;

2)алгоритмическая надежность, т.е. алгоритм должен приводить к желаемому результату, если соблюдены все условия его приме­нения;

3)достаточная точность результата;

4)умеренные затраты машинного времени и памяти.

Основные характеристики:

1) Точность интегрирования.

2)Численная устойчивость метода.

3)Стратегия выбора шага

Точность интегрирования. Определяется полной ошибкой на каждом m -м шаге интегрирования; i - номер элемента вектора x ; n - означает "полная" ошибка. Эту ошибку можно определить,если известно точное решение, что, конечно, не имеет места в действительности. Поэтому обычно рассматривают основные составляющие полной ошибки.

1. Ошибка аппроксимации - погрешность собственно метода интегрирования. Ее величина определяется способом замены производной конечно-разностными выражениями в формуле интегрирова­ния (2.3) (т.е. способом замены функции F(x,t) на отрезке )

2. Ошибка вычислений связана с ошибками округления чисел в ЭВМ.

3. Ошибка накопления равна полной ошибке на предыду­щем шаге. Ее источник - вычисление на основе приближен­ного значения , а не точного.

Как определить эти ошибки? Начнем с последних двух. яв­ляется случайной величиной со сложным характером изменений. Прак­тика расчетов показывает, что эта ошибка мала. Например, если вы­числения осуществляются с точностью - , то этой составля­ющей можно пренебречь.

Ошибку оценить нельзя, так как не известна полная ошибка на предыдущем шаге . Однако можно попытаться оценить характер ее поведения от шага к шагу. Если метод интегрирования численно устойчив, то эта ошибка не увеличивается с ростом m и по величине много меньше ошибки аппроксимации. Таким образом, надо оценить ошибку .

Ошибка аппроксимации равна разности между точным решением и численным, полученным из точки по используемой формуле интегрирования. Точное решение при малом можно разложить в ряд Тейлора в точке :

(2.6)

Тогда формула интегрирования будет аппроксимировать только первые члены ряда Тейлора.

Порядком точности S (порядком аппроксимации или степенью) метода интегрирования называется порядок производной в том члене ряда Тейлора, до которого формула интегрирования аппроксимирует ряд Тейлора (2.6) при . Например, явный метод Эйлера

(2.7)

аппроксимирует ряд (2.6) до членов первого порядка производной и поэтому S=1.

Ошибку интегрирования можно определить путем оценки величины суммы оставшихся членов ряда Тейлора. Для метода Эйлера пропорциональна величине , так как при более вы­сокие степени много меньше.

Для определения реальной ошибки аппроксимации в процессе ин­тегрирования используется правило Рунге, которое является наиболее универсальным

,

где С - некоторая константа; - значение полученное в точке повторным расчетом данным методом интег­рирования от точки за два шага, каждый из которых равен .Этот метод, однако, требует больших вычислительна затрат. Поэто­му часто используют другие способы, более простые, о которых бу­дет сказано ниже,

Устойчивость методов численного интегрирования. Если не возрастает с увеличением числа шагов, то используемый метод интег­рирования называется численно устойчивым при данном шаге . Если даже при небольших значениях ошибок аппроксимации вычислений растет шаг от шага, то используемый метод численно неустой­чив при данном шаге .Численная устойчивость зависит не только от метода, но и от характера решаемой задачи. Рассмотрим два случая для линейной сис­темы (1.5), положив u=0.

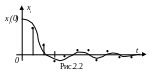
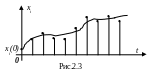
Случай 1. Система (1.5) асимптотически устойчива (рис. 2.2). Сплошной линией показано точное решение системы (1.5), точками - ее приближенное ре­шение, полученное с помощью какого-либо численного метода интегрирования. Очевидно, что приближенное решение должно отслеживать точно с некоторой допустимой ошибкой. Это значит, что дискретная система (2.2), описывающая метод интегрирования также должна обладать свойством асимптотической устойчивости. В этом случае численный метод называется абсолютно устойчивым.

Случай 2. Система (1.5) неустойчива. Значит, и дискретная система (2.2) также должна быть неустойчивой, но скорость изменения близка к скорости изменения , чтобы решения были также близки. В этом случае численный метод называется относительно устойчивым.

Выбор величины шага интегрирования.

Эффективность метода во многом зависит от стратегии выбора шага в процессе интегрирования. При увеличении растет да и метод может стать неустойчивым. Однако слишком маленький шаг увеличивает вы­числительные затраты. Ошибка аппроксимации производной в формуле интегрирования зависит от скорости изменения x(t), т.е. от ве­личины функции F(x,t). Поэтому, чтобы поддерживать ошибку на допустимом уровне, шаг должен корректироваться в процессе интегрирования в зависимости от величины F(x,t). Область, в ко­торой можно варьировать шаг, зависит от величины области числен­ной устойчивости метода. Способы выбора шага будут рассмотрены ниже.