5.8. Произведение разреженной матрицы общего вида и заполненного вектора-столбца

Результатом этой операции является заполненный вектор С причем, символический этап отсутствует.

Алгоритм рассмотрим на конкретном примере:

IA = 1 3 7 9 11

JA = 5 3 4 3 15 16 42 RR(C)U

AN = -1 2 3 3 4 7 -21 11.

Заполненный вектор = (2 1 3 4 7 3)

Обработка с троки 1

1. Просматриваем массив IA и обнаруживаем, что первая строка матрицы А соответствует первому и второму элементу массива JA : JA(1)=5 и JA(2)=3 , т.е. ненулевыми являются элементы - и

2. Просматриваем массив AN и устанавливаем, что =-1 и =2

3. Обращаемся к вектору b , выбирая из него соответственно = 7 и 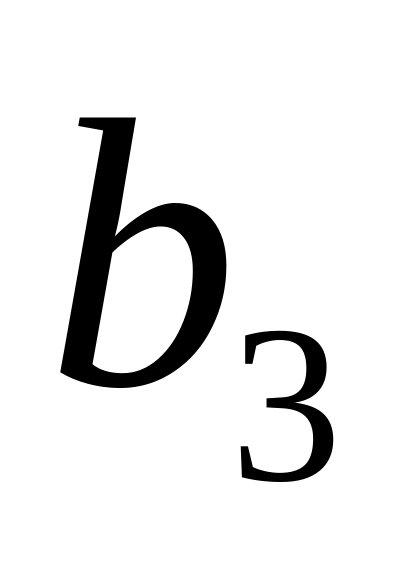= 3 .

4. Вычисляем C(1)=(-1)*(+7)+2*3=-1

Обработка строки 2.

1) Просматриваем массив IA дальше и устанавливаем, что вторая строка матрицы A начинается с 3-го и заканчивается 6-м элементом массивов JA и AN , т.е. ненулевыми являются элементы , , и второй строки.

2) Просматриваем массив AN , начиная с 3-го и кончая 6-м элементом и устанавливаем, что , , и

3) Обращаемся к вектору b , выбирая из него , и

4. Вычисляем С(2) = 3*4 + 3*3 + 4*2 + 7*7 = 78.

Обработка строк 3 и 4 осуществляется аналогично. В результате С(3) = -7 и С(4) = 5. Вектор = (-1 , 78, -7,5), (Мерность подученного вектора соответствует умножению матрицы A размером 4 * 6 и вектора b размером 6 * 1.)

5.9. Произведение двух разреженных матриц

Предположим, что обе матрицы заданы в формате RR(C)U Сложность выполнения традиционного алгоритма умножения двух матриц состоит в том, что доступ к столбцам матрицу B затруднен. Имеется два выхода из этого положения:

а) транспонировать матрицу В и умножать строку матрицы A на строку матрицы В ;

б) изменить порядок накапливания суммы для формирования элементов матрицы С .

Обсуждаем второй способ. Рассмотрим умножение двух матриц A и B

Обычный способ:

Будем формировать элементы не сразу , как это показано выше (для чего, действительно, надо иметь доступ, к столбцам матрицы B), а постепенно накапливая суммы, обращаясь только к строкам матрицы B. Для этого введем два скалярных вещественных накопителя: и . Обнулим их сначала: .и . Затем занесем в - , а в - произведение получим:

и

При этом мы обратились к 1-й строке матрицы B . Для формирования и надо взять из матрицы A элемент из той же строки и умножить его на элементы второй строки матрицы b , и тогда получим:

и

Далее выполним присваивание:

и

Для получения элементов второй строки матрицы С надо элемент сначала умножить на элементы первой строки матрицы B , а затем элемент - на элементы второй cтроки:

и

Затем к этим значениям прибавить новые произведения:

и

Очевидно, что и .

Подведем итог : элемент матрицы A последовательно умножается на все элементы строки второй матрицы, легко доступные, если вторая матрица задана в строчном формате. Заметим, номер строки матрицы В , на элементы которой надо умножать определяется номером j.

Как и ранее, алгоритм умножения двух матриц распадается на два этапа: символический и численный.

Символический этап . Исходная информация - портреты и мерности матриц А и B : IА , JA , IB, JB, NP, NQ, NR (матрица А размерности и матрица B размерности q×r ). Нужно найти портрет результирующей матрицы С : IC, JC.

Выполнение алгоритма обстоит из следующих шагов:

1)берется строка I матрицы A , т.е. рассматривается массив столбцовых индексов 1-й строки -в определенном массивом IА месте;

2)для каждого столбцового индекса J в строке 1 матрицы A просматриваются столбцовые индексы отроки J матрицу B , т.е. массив JB в соответствующем месте;

3) в массиве JС производится слияние столбцовых индексов всех строк матрицы В , номера которых указаны в массиве JА , в том месте, где описана 1-я строка.

В дальнейшем для, удобства будем пользоваться следующим обозначением:

- та часть массива JА которая относится к 1-й строке. Например, или и т.д.

Рассмотрим умножение матриц A и B на примере:

IA = 1 3 7 9 11

JA = 5 3 4 3 1 5 16 42

AN = -1 2 3 3 4 7 -2 -1 11

IB = 1 3 6 8 10 12 14

JB = 21 421 3 1 42 32 14

BN = -12 81-1 -21 89 12 6-1

NP = 4

NQ = 6

NR = 4

Ввиду громоздкости алгоритма, рассмотрим его для одной стро­ки матрицы А , например второй. Покажем,, как формируется вторая строка матрицы С , т.е. соответствующие этой строке элементы мас­сива JС . Как упоминалось ранее, для этого надо выполнить слияние строк матрицы B номера которых определяются столбцевыми индексами второй строки матрицы А . Для этого воспользуемся массивом переключателей IX, длина которого определяется количеством столб­цов матрицы В , т.е. NR Алгоритм выглядит следующим образом.

1). Обнуляем массив IX:

IX = 0 0 0 0

2)Находим часть массива JA , соответствующую второй стро­ке: = 4 3 1 5.

Следовательно, надо слить cписки столбцовых индексов 4-й, 3-й, 1-й и 5-й строки матрицы В .

3)Заносим список 4-й строки матрицы В в ту часть массива JC , которая будет соответствовать второй строке, т.е. просто после списка столбцовых индексов первой строки матрицы С запи­сываем = 4 2;

JС = ….4 2

4).Заносим единицы в массив IX:

IX = 0 I 0 I

5. Производим слияние столбцовых индексов третьей строки матрицы В с имеющимся в списком:

= 3 1

Так как IX(3)=0 и IX(1)=0, то заносим эти индексы в массив JС :

=….4 2 3 1

6)Заносим единицы в массив IX = 1 1 1 1.

7)Производим слияние столбцовых индексов 1-й строки матрицы B с имеющимся в списком:

2 1.

Так как IX(2)=1 и IX(1)= 1, в описке уже есть номера 2 и 1. На этом этапе не меняется.

8)Производим слияние столбцовых индексов 5-й строки матри­цы В с имеющимся в списком:

3 2 . Так как IХ(3) = 1 и IХ(2) = 1, в списке уже есть номера 3 и I, значит, не меняется и окончательно имеет вид:

= 4 2 3 1.

Аналогично вычисляются столбцовые индексы всех оставшихся строк матрицы JС. Массив IС формируется так же, как это уже было опи­сано ранее: 1-я цифра всегда 1, а затем к ней и к каждой следую­щей прибавляется количество столбцовых индексов очередной строки. Последняя цифра указывает номер первой пустой позиции в массиве JC (а затем и CN).

Численный этап. Задано; IА , JA , AN, IB, JB, BN, IC.

Для вычисления значений-элементов строк матрицы С тре­буется вещественный накопитель X длины NR (по числу элементов в строке). Алгоритм вычисления значений элементов 1-й строки С состоит в следующем.

1)Обнуляем те элементы массива X номера которых указаны в 2) Обращаемся к подмассиву и первый его ненулевой J-элемент заносим в ячейку АА.

3) Обращаемся к J -и отроке матрицы В : Умножаем эле­менты подмассива на АА. Результат заносим в вещественный на­копитель X на те места, которые указаны в

Аналогичные действия проводим для всех столбцовых индек­сов . При этом каждый раз прибавляя частичные произведения к уже имеющимся суммам в накопителе X ; В результате в массиве X мы будем иметь 1-ю строку матрицы С , т. е, подмассив .

Проделаем указанные действия для 2-й строки матрицы А наше­го примера. Для этого введем массив X длиной NR=4.

1) Обнуляем все четыре элемента массива X , так как =4 2 3 1 т. e ; в списке столбцовых индексов содержатся все воз­можные значения от I до 4:

X = 0 0 0 0

2) Обращаемся к массиву его первый ненулевой элемент равен 3, значит ,AA= 3. Столбцовый индекс, соответствующий этому элементу, находится в подмассиве и равен 4,

3) Обращаемся к 4-й строке матрицы B , т.е к и умно­жаем ее элементы на AA= 3, получим:

= 8 9

3* = 24 27

Результат заносим в вещественный накопитель X на те места кото­рые указаны в = 4 2.

X=0 27 0 24

4) Обращаемся снова к массиву ; его второй элемент также равен 3, значит AA= 3. Столбцовый индекс, соответствующий этому элементу, находится в подмассиве на втором месте и ра­вен 3,

5) Обращаемся к 3-й отроке матрицу B , т.е. к и умнажаем ее элементы на AА =3, получим:

= -2 1

3* = -6 3

Результат прибавляем к тем элементам массива X , номера которых указаны в = 3 1

Х = 3 27 - 6 24 .

6) Обращаемся снова к массиву , его 3-й элемент равен 4, т.е. AA= 4. Его столбцовый индекс находится в и равен 1.

7) Обращаемся к 1-й строке матрицы В , т.е. к , и ум­ножаем ее элементы на AA = 4.

= -1 2

4* = -4 8

Результат прибавляем к тем элементам массива X , номера которых указаны в = 2 1

8) Обращаемся снова к массиву , его 4-й элемент равен 7, т.е.AA= 7. Его столбцовый индекс находится в и равен 5.

9) Обращаемся к 5-й строке матрицы B , т.е. к и умно­жаем ее элементы на AA= 7:

= 1 2

7* = 7 14

Результат прибавляем к тем элементам массива X , номера которых указаны в = 3 2

X= 11 37 1 24

Значения элементов массива X переписываем в . Итогом символи­ческого и численного этапов для строки 2 матрицы С будем иметь:

JС = ……4 2 3 1….

CN = ……11 37 1 24 …..