4. Решение систем линейных ау
4.1. Метод Гаусса
Рассмотрим систему
Ax=b (4.1)
где А - неособенная матрица n*n; b,x - векторы мерности n. Для систем (4.1) с плотными матрицами не найдено алгоритмов решений, для которых доказано, что они лучше по времени и точности чем метода исключения Гаусса. Гауссовское исключение существует во многих вариантах, которые алгебраически тождественны. Методы отличаются способами хранения матриц, порядком исключения, способами предупреждения больших погрешностей округления и тем, как уточняются вычисленные решения. Имеются также варианты, специально приспособленные для положительно определенных матриц A.
Алгебраической основой гауссова исключения является следующая теорема, которую приведем без доказательства[8].
LU-теорема.
Пусть дана квадратная матрица A
порядка n
и
означает
главный минор матрицы, составленный
из k
строк и столбцов. Предположим, что
.
Тогда существует единственная
нижнетреугольная матрица
где
, и единственная верхнетреугольная
матрица
, такие, что LU=A.
Более того
Тогда, система (4.1) может быть записана как LUx=b и сведется к двум системам о треугольными матрицами
Ly=b и Ux=y, которые легко решить.
Прямой ход Гаусса. Вычисление L и U вместе с решениям системы Ly=b обычно называется прямым ходом метода Гаусса, имеет (n-1 ) шагов. Основная идея состоит в том, чтобы подучить верхнетреугольную матрицу U и пересчитать вектор b , который является решением системы Ly =b относительно y . Рассмотрим случай n=4 .
Шаг 1.
Исключаем из всех уравнений, кроме
первого,
.
Для этого первое уравнение умножаем
на
и вычитаем его последовательно из
2-го, 3-го и 4-го уравнений. Таким образом,
получим три уравнения, в которых нет
:
(4.2)
где
,
,
При этом в преобразовании уравнения (4.1) к виду (4.2) участвовала матрица
Шаг 2. Исключаем из
системы (4.2) Переменную
.
Для этого умножаем 3-е и 4-е уравнение
на
.
Тогда умножаем
и
на
матрицу
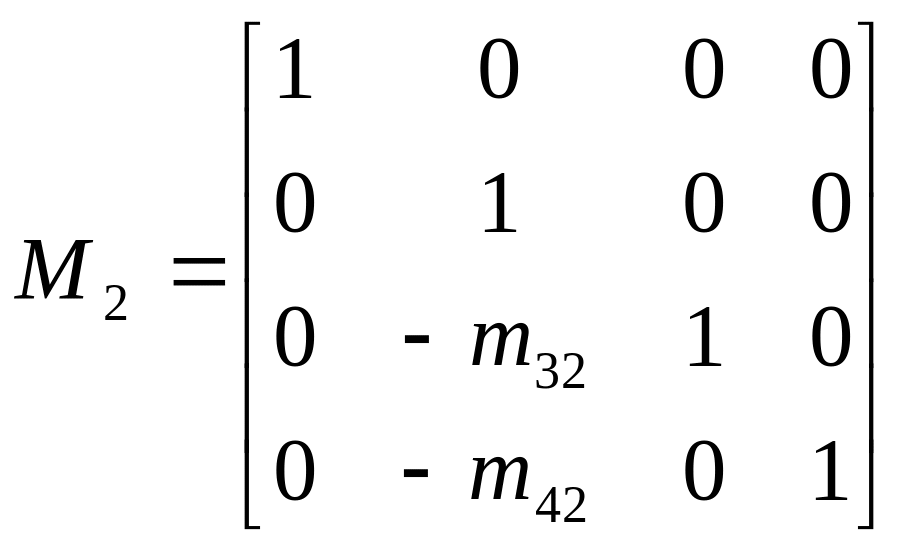
для получения
и
.
В системе
переменная
есть только в первом уравнении, а
- в первом и втором.
Шаг З.
Исключение переменной
.
Вычисляем
и умножаем
и
на матрицу
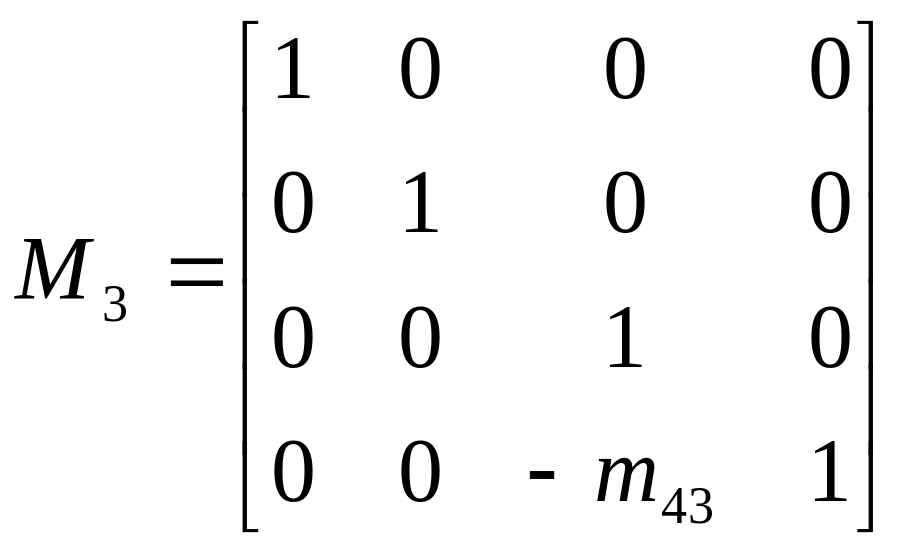
и
-
есть верхняя треугольная матрица U,
что Дает систему уравнений следующей
структуры:
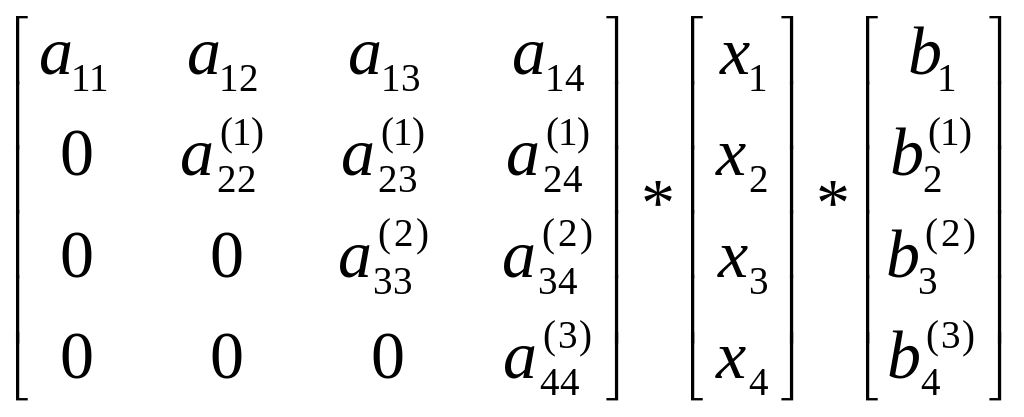(4.3)
Пусть
, тогда
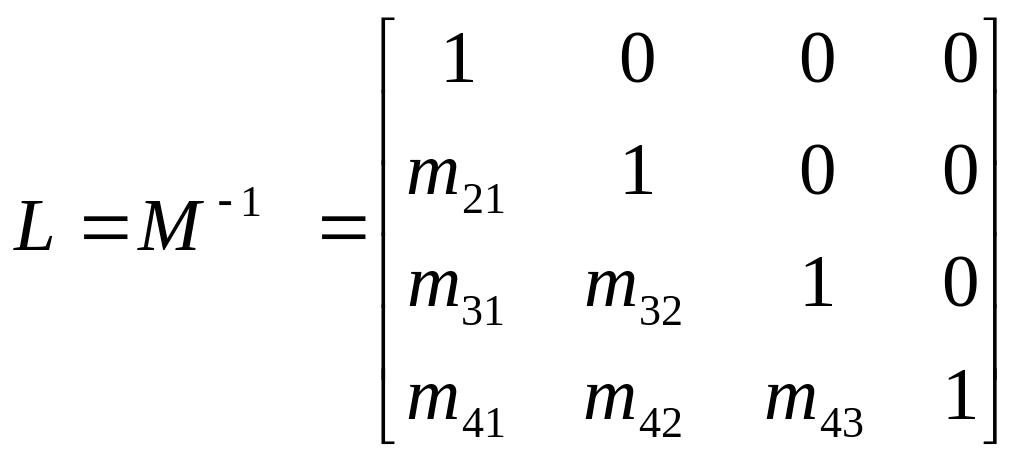
а вектор у - есть столбец правой части в системе (4.3), который мы нашли, выполняя прямой ход Гаусса.
Обратный ход состоит
в решении системы (4.3) снизу вверх:
сначала находим,
подставляем его в третье уравнение
и решаем его относительно
и так далее до
.
Обратный ход имеет n
шагов.
Для произвольного k метод Гаусса может быть представлен следующими формулами:
Прямой ход.
Здесь k
- номер шага,
(4.4)
Обратный ход.
Из последнего уравнения находим
.
Остальные неизвестные находится последовательно по формуле
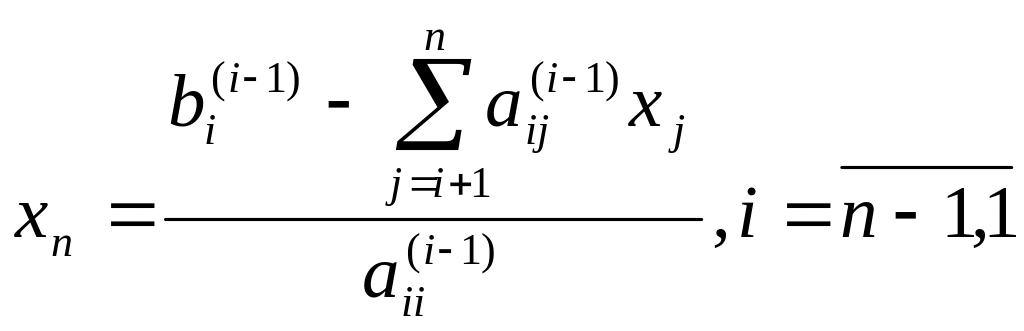(4.5)