Отрицание.
Определение. Отрицание – унарная логическая операции (т.е. применимая к одному высказыванию). Отрицание соответствует конструкциям «Не …», «Неверно, что …».
Отрицание высказывания
а обозначается
и определяется следующей таблицей
-
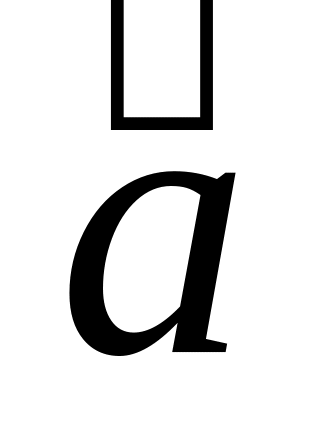
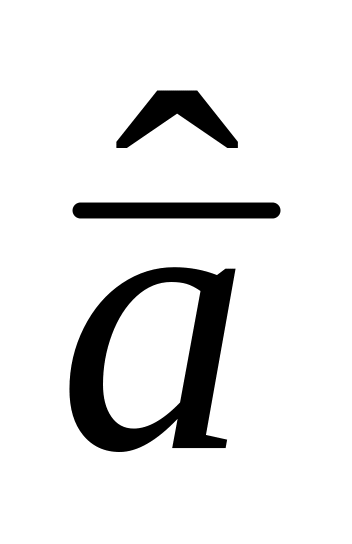
0
1
1
0
Очевидно,
имеет место
свойство
.
Это свойство называется законом двойного отрицания.
Перейдем далее к определению бинарных (т.е. применимых к паре высказываний) операций.
Конъюнкция.
Конъюнкция (логическое умножение) соответствует союзу «и» в русском языке.
Определение.
Конъюнкцией
высказываний a
и b называется
высказывание, обозначаемое
и определяемое следующей таблицей
0 0 0
0 1 0
1 0 0
1 1 1
т.е.конъюнкция a
Имеют место следующие свойства:
a
b
≡ b
a
a
1
≡ a
a
0
≡ 0
a
a ≡ a
- закон идемпотентности.
b
истинна тогда и только тогда, когда
истинны оба высказывания а и b.
Дизъюнкция.
Дизъюнкция (логическое сложение) соответствует неразделительному «или» в русском языке.
Определение.
Дизъюнкцией
высказываний а и b
называется высказывание, обозначаемое
a
b
и определяемое следующей таблицей
0 0 0
0 1 1
1 0 1
1 1 1
т.е. дизъюнкция ложна тогда и только тогда, когда ложны оба высказывания а и b.
Имеют место следующие свойства:
a b ≡ b a – коммутативность
a 1 ≡ 1/
a 0 ≡ a,
a a ≡ a – закон идемпотентности.
Эквиваленция
Эквиваленция (равносильность) соответствует в русском языке конструкции «тогда и только тогда».
Определение.
Эквиваленцией высказываний a и b называется высказывание, обозначаемой a ~ b (a ↔ b) и определяемое следующей таблицей:
0 0 1
0 1 0
1 0 0
1 1 1
Отсюда следует, что эквиваленция истинна тогда и только тогда, когда образующие ее высказывания a и b имеют равные значения истинности.
Имеют место следующие свойства:
а ~ b ≡ b ~ a – коммутативность.
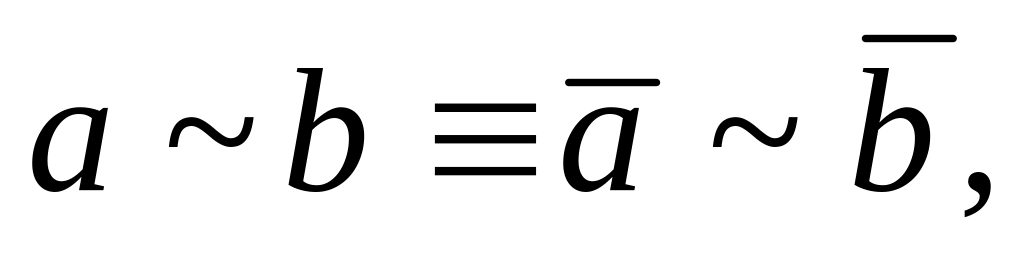
a ~ 1 ≡ a.
a ~ 0 ≡
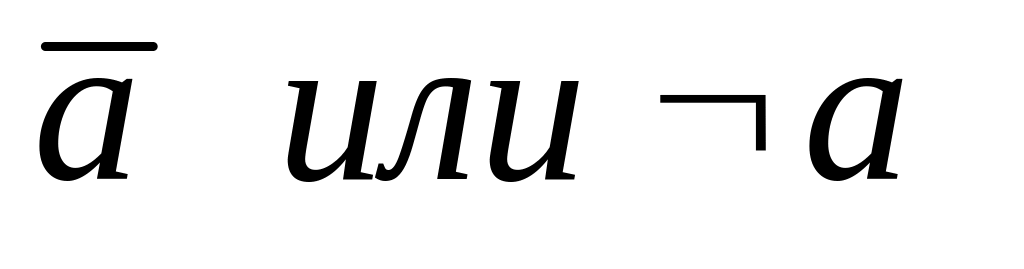
Импликация.
Импликация соответствует конструкции «Если …. то».
Определение.
Импликацией высказываний a
и b
называется высказывание, обозначаемое
a → b
(
и определяемое следующей таблицей
0 0 1
0 1 1
1 0 0
1 1 1
т.е. импликация ложна тогда и только тогда, когда a – истина, а b – ложь.
a – посылка, b − заключение.
Восприятию определения импликации сопротивляется, хотя в математике оно очень часто нами используется. Из арифметики известна теорема «если целое число делится на шесть, то оно делится на два» − высказывание Q. Высказывание а(x) – «число делится на шесть»; высказывание b(x) – «число делится на два», тогда Q(x) ≡ a(x) → b(x). Ясно, что при x = 6, 2, 3 реализуются четвертая, вторая и первая строки. Однако, нельзя подобрать число для третьей строки.
Но можно привести и другие примеры. Например, «если сын сдаст сессию на отлично, то отец купит ему машину. В нашем случае события а и b могут быть концептуально совсем не связаны. Возможны импликации вида «Если сегодня четверг, то 2 х 2 = 5». Эта импликация верна во все дни, кроме четверга.
Приведенные операции не являются независимыми. Одни из них могут быть выражены через другие.
Теорема 1.Справедливы следующие равносильности:
Докажем с помощью таблицы истинности первое соотношение.
0 0 1 1 1
0 1 1 1 1
1 0 0 0 0
1 1 0 1 1
Справедливость первого соотношения доказывается тождественностью последних столбцов.
Из
приведенных равносильностей видно, что
→ и ~ выражаются через
Можно
показать, что через операции 
можно выразить любую операцию алгебры
высказываний. Поэтому в дальнейшем
основное внимание уделяется этим
операциям, которые называются булевскими
(булевыми) операциями алгебры
высказываний. Джордж Буль (1815 – 1864) –
английский математик, основатель
символической логики, которую теперь
принято называть булевой алгеброй.
Теорема 2. Справедливы следующие равносильности для булевой алгебры высказываний:
