Похибки непрямих вимірювань

Нижче приводяться теореми (без доказів), що дозволяють обчислити похибки побічно вимірюваних величин.

1. Абсолютна похибка суми дорівнює сумі абсолютних погрішностей доданків. Так, якщо X=а+b, де а і b величини, які можна виміряти прямим методом з погрішністю ±∆a і ±∆b, то ∆Х=∆а+∆b, оскільки ∆а і ∆b мають подвійний знак, то при підсумовуванні ∆а і ∆b їхні знаки підбираються так, щоб ∆Х було максимальним.

2. Абсолютна похибка різниці дорівнює сумі абсолютних погрішностей зменшуваного і від'ємника.

Нехай X=а-b, тоді ∆Х=∆а+∆b. Правило вибору знаків ∆а і ∆b те ж, що й у випадку 1. Слід зазначити, що це правило застосовне до усіх випадків обчислення погрішностей побічно вимірюваних величин.

3. Знайдемо абсолютну похибку добутку Х=аb. Нехай а±∆а, b±∆b, тоді ∆Х=а∆b+b∆а.

Абсолютна похибка дробу (при а ± ∆а і b ± ∆b) дорівнює

.

З цих часткових теорем можна зробити висновок, що середні абсолютні похибки побічно вимірюваних величин знаходяться за правилами диференціювання формул, що зв'язують ці величини з тими, котрі вимірюють прямим шляхом. Необхідно тільки знак замінити знаком ∆ і вибрати знаки абсолютних погрішностей прямим шляхом вимірюваних величин так, щоб похибка непрямого вимірювання була максимальною. Слід зазначити, що після диференціювання вихідних залежностей і одержання формул погрішностей варто відкинути члени, утримуючі величини другого і більше порядку малості (тобто члени, утримуючі добутки ∆а∆b).

Відносна похибка непрямих вимірювань дорівнює

.

Однак, з іншого боку,

або .

Таким чином, відносну похибку можна знайти шляхом логарифмування вихідного виразу і його наступного диференціювання із заміною знака  на знак ∆ і відповідним вибором знаків при абсолютних погрішностях прямих вимірювань.

По відносній похибці можна, надалі, знайти абсолютну похибку будь-якої складної залежності шляхом простих формальних операцій. Наприклад, нехай

, ,

,

.

Як бачимо, методом диференціального логарифма для знаходження абсолютних погрішностей користуватися зручніше і простіше, ніж методом простого диференціювання.

2 Елементи сучасної теорії погрішностей

При описі багатьох фізичних явищ неможливо прогнозувати точне поводження окремих фізичних подій. Однак їх можна описати, скориставшись поняттями "середнє поводження" чи "імовірність".

Теорія ймовірностей заснована на припущенні, що частота появи окремого результату в процесі експерименту прямує до кінцевої межі. Ймовірність Р(А) деякого результату А дорівнює частоті його появи

,

де: N- загальне число чи досвідів спостережень,

n(N) - число появ A під час цих іспитів. У фізику часто імовірність можна визначити трохи інакше

,

де: ∆t - час спостереження результату A ,

Т - повний час експерименту.

Незважаючи на те, що ці визначення не дуже зручні (N і T( ( ), практично для визначення імовірності надходять саме так (проробляють багато досвідів), причому чим більше N (чи Т ), тим точніше визначається імовірність.

Результат А (випадкова величина, тобто для появи її неможливо знайти чи причину причин занадто багато і їхній вплив важко врахувати) може мати як дискретне значення, так і приймати нескінченно близьких значень (безупинний спектр). В останньому випадку характерна особливість: імовірність окремої події, що полягає в тім, що виникає саме результат А (визначене значення) дорівнює нулю (близька до нуля). Тому можна говорити лише про ймовірність того, що випадкова величина може знаходитися в інтервалі ∆Х значень від Х до X+∆Х. Ймовірність d(X) того, що випадкова величина приймає значення від Х до X+dХ, залежить від самого Х, (тобто є деякою функцією f(X) і від величини .

Сукупність усіх значень ймовірностей даної величини утворює розподіл даної випадкової величини f(Х). Це функція розподілу ймовірності. Вона показує як розподіляється ймовірність на d в залежності від Х

і часто називається густиною ймовірності (рис.1). Звичайно f(X) виражається у вигляді графіка, по якому можна судити про величину d(X) (площа заштрихованої ділянки під f(X) є основою d) на d.

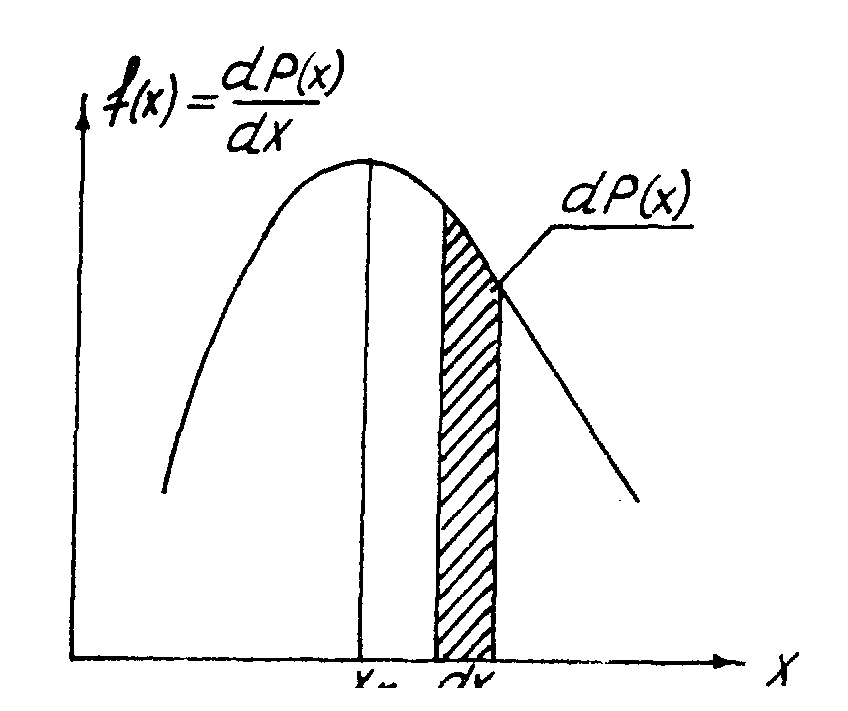
Рисунок 1 - Графік функції розподілу ймовірності в залежності від Х.

Значення випадкової величини, що відповідає максимуму f(X) називається найімовірнішим.

В теорії ймовірностей і її додатків важливу роль відіграє диференціальний закон розподілу густини ймовірності випадкової величини, що має вигляд:

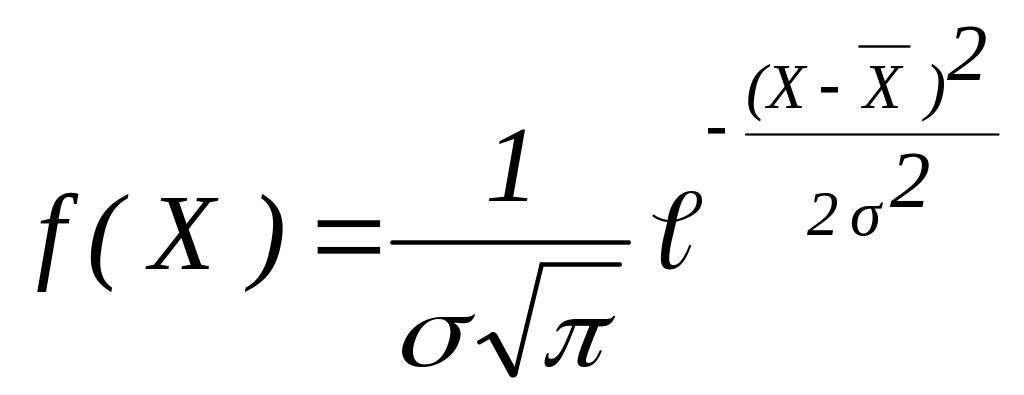
для дискретного ряду величин, де - середнє значення чи математичне очікування

,

- для випадкової величини, безперервно розподіленої (Х змінюється безперервно), σ² - дисперсія випадкової величини. Якщо

,

тоді

.

Це середнє квадратичне відхилення називається дисперсією випадкової величини. Дисперсія визначає гостроту кривої f(Х). Форма кривих Гауса (нормальний закон розподілу) представлена на рис.2 (для різних значень дисперсії).

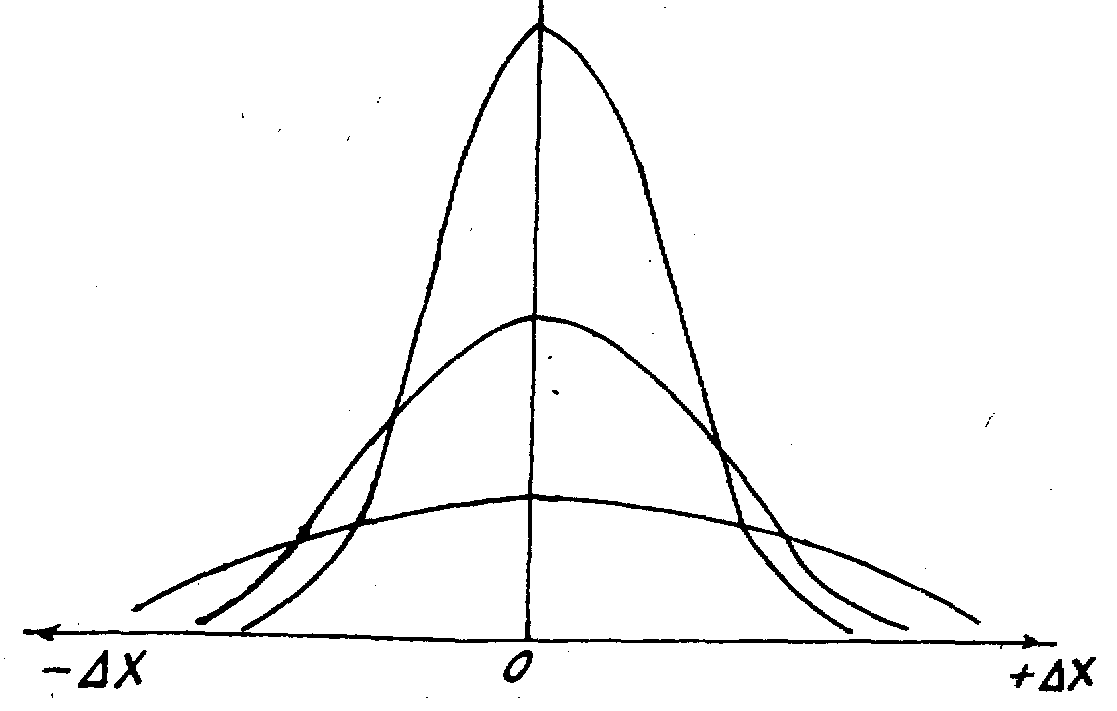
Рисунок 2 - Форма кривих Гауса для різних значень дисперсії.

При вимірюваннях фізичних величин у тих випадках, коли основну роль відіграють випадкові помилки, всі оцінки точності вимірювання можна зробити тільки з деякою ймовірністю. Для того, щоб виявити випадкову помилку вимірювань, їх необхідно повторити кілька разів. Якщо кожне вимірювання дає результати, трохи відмінні від інших, випадкова помилка відіграє істотну роль. За найбільш ймовірне значення вимірюваної величини варто прийняти її середнє арифметичне значення за умови, що при великому числі вимірювань помилки однакової величини, але різного знака - рівноймовірнісні. Якщо помилки можуть приймати безупинний ряд значень і частота появ помилок зменшується зі збільшенням помилки при рівноточних (з однаковою старанністю проведених) вимірюваннях, то крива розподілу випадкових погрішностей описується кривою Гауса (нормальний закон розподілу випадкових величин).

,

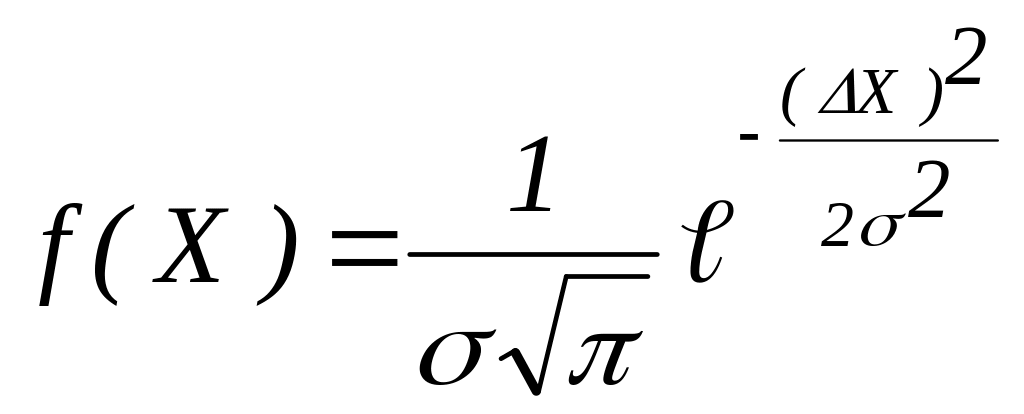∆X - величина випадкової похибки, імовірність якої оцінюється f(X)=Y Таким чином, для характеристики похибки необхідно знати величину похибки ∆Х (∆Х називають довірчий інтервал) і величину імовірності того, що результат вимірювань характеризується даною погрішністю ∆Х (довірча чи імовірність коефіцієнт надійності ). Вказівка однієї похибки без указівки коефіцієнта надійності в значній мірі позбавлено змісту.

Для одержання чисельних результатів застосовуються таблиці нормального розподілу щільності імовірності, але щоб ними скористатися, необхідно нормувати f(X)

,

де довірчий інтервал, виражений у частках середньої квадратичної помилки.

Нормована функція нормального розподілу імовірності

- функція Лапласа (інтеграл ймовірностей). Так, наприклад, середній квадратичній помилці відповідає довірча імовірність 0,68 (=1), подвоєній середній квадратичній помилці (2) - довірча імовірність 0,95 (або 95 %) і т.д.

Часто, указуючи для оцінки похибки величину σ, не дають значення довірчої ймовірності, вважаючи її відомою величиною (68%).

Припустимо, вимірювана величина Z є сума (чи різниця) Х і У, результати вимірювання яких незалежні, - їхні дисперсії, тоді

.

Таким чином, для перебування сумарної помилки потрібно складати не самі помилки, а їхні квадрати (S_Z - середня квадратична помилка суми).

Нехай Х₁, Х₂, Х₃...,Х_n - результати окремих вимірювань, причому кожне з них характеризується однієї і тією же дисперсією S.

Середнє з них

.

Дисперсія ,

.

Отже

Тоді середня квадратична похибка S_Y середнього арифметичного Y дорівнює середньої квадратичної похибки окремого результату, діленої на корінь квадратний з числа вимірювань. Тобто збільшуючи число вимірювань, можна значно зменшити похибка, не прибігаючи до поліпшення точності (зменшенню S чи σ, що визначається методикою вимірювань). Нормальний закон розподілу випадкових погрішностей добре виконується при досить великому числі вимірювань (кілька сотень) і дозволяє оцінити параметри його: σ² для заданого ∆Х, чи ∆Х по заданому σ².

Якщо ж число вимірювань невелике (менш двадцяти), то ці задачі можна вирішити, скориставшись іншим законом розподілу ймовірностей випадкових величин - розподілом Стьюдента. Він має вигляд

.

Тут , де ∆X - абсолютна похибка результату серій вимірювання, σ - середньоквадратична похибка результату тієї ж серії вимірювань, Г(n) – гама функція. При n→ (n→20) цей розподіл переходить у розподіл Гауса.

При малому числі вимірювань для розрахунку ∆Х при заданій надійності  використовують коефіцієнт Стьюдента t_, що залежить від числа вимірювань n і величини 

,

де

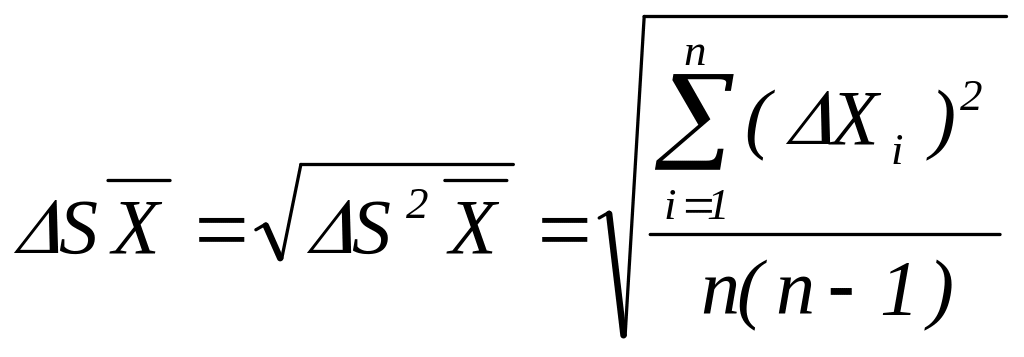
- середньоквадратична похибка результату серій вимірювань. Задаючи надійність, тобто припускаючи  рівним визначеній величині, по числу вимірювань n знаходимо в таблиці значення коефіцієнта Стьюдента. Визначивши ∆S , знаходимо ∆X

.

Результат можна записати у вигляді

.

На закінчення пропонується зразковий порядок операцій для оцінки похибки прямих вимірювань.

1. Обчислюється середнє значення з n вимірювань

.

2. Знаходяться похибки окремих вимірювань

.

3. Обчислюються квадрати погрішностей окремих вимірювань (∆X_i)².

4. Якщо є вимірювання, що відрізняються різко за своїм значенням від інших, перевірити чи не є вони промахами.

5. Знаходять середню квадратичну похибку серії вимірювань

.

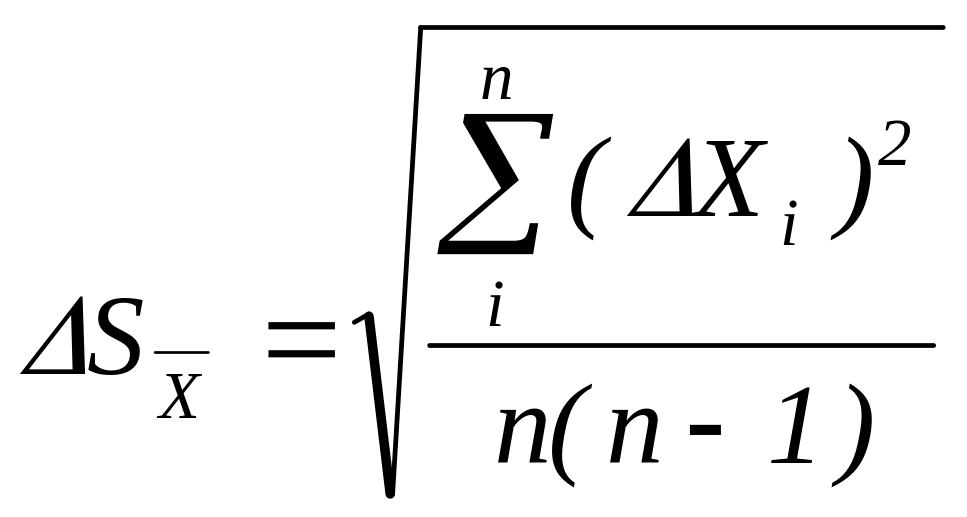6. Задається коефіцієнт надійності .

7. Визначається коефіцієнт Стьюдента t_(n) для даного n і  за таблицею.

8. Знаходять границі довірчого інтервалу (похибка результату вимірювань)

.

9. Записується остаточний результат

.

10. Визначається відносна похибка серії вимірювань - величина, що характеризує точність вимірювань

.