§6. Задача Больца.

Так называют задачу исследования на экстремум функционала вида

,

где - дифференцируемая функция двух переменных, рассматриваемого на множестве . Аналогично простейшей задаче для первой вариации имеем представление

(6.1)

где . Применяя принцип Ферма, т.е. приравнивая полученное выражение к нулю, воспользуемся произволом в выборе функции h(x), а именно ограничимся лишь функциями h(x) из , такими, что h(0) = h(1) = 0. На множестве таких функций мы имеем , откуда вследствие леммы Дю- Буа- Реймона вытекает, что искомая функция должна удовлетворять равенству

(6.2)

продифференцировав которое, получим уравнение Эйлера

. (6.3)

Но тогда выражение (6.1) должно приобрести вид

.

Приравнивая его к нулю и пользуясь произвольностью выбора функции h(x), точнее произвольностью чисел h(0), h(1), имеем

(6.4)

(6.5)

С другой стороны, подставим в тождество (6.2) значение x=1 и выразим c. Тогда равенство (6.4) примет вид

| + . (6.6)

Аналогично, если подставить в (6.2) x=0 и выразить константу, то равенство (6.5) примет вид

| =0. (6.7)

Тем самым мы получили два краевых условия (6.6), (6.7), дополняющих уравнение Эйлера.

§7. Задача Пуассона.

Ставится задача исследования на экстремум функционала

, (7.1)

рассматриваемого на множестве G n раз непрерывно дифференцируемых на [0,l] функций, удовлетворяющих равенствам

, . (i=0,…, n-1) (7.2)

Предполагается достаточная гладкость решения u(x) этой задачи и функции F:[0,l] . Первая вариация, как легко проверить, имеет вид

(7.3)

при любом h из множества n раз непрерывно дифференцируемых на [0,l] функций, удовлетворяющих равенствам

, . (i=0,…, n-1) (7.4)

Преобразуя в (7.3) i- ое слагаемое i-кратным интегрированием по частям, имеем

Здесь в силу (7.4) все внеинтегральные слагаемые обращаются в нуль. Подставляя полученное выражение в (7.3) и пользуясь принципом Ферма, имеем

(7.5)

Далее нам потребуется следующая

Лемма 7.1 (Лагранж) Пусть функция A(x) непрерывна на отрезке [0,l], и пусть для любой функции выполняется равенство

Тогда A(x)=0.

Доказательство. В предположении противного существует точка на отрезке [0,l], в которой . Но тогда, в силу непрерывности A(x), существует и некоторый интервал , на котором A(x) строго положительна или строго отрицательна. Возьмем в функцию , которая строго положительна в и тождественно равна нулю вне . В качестве такой функции можно, например, взять «шапочку». Тогда причем последний интеграл отличен от нуля, так как его подынтегральное выражение на нулей не имеет. Лемма доказана.

Применив лемму 7.1. к равенству (7.5), получим

(7.6)

Уравнение (7.6) называют уравнением Эйлера – Пуассона.

Упражнения.

Найдите допустимые экстремали (т.е. решения уравнения Эйлера – Пуассона, удовлетворяющие указанным условиям) для заданных функционалов:

7.1.

7.2. , , ,

7.3 , , , .

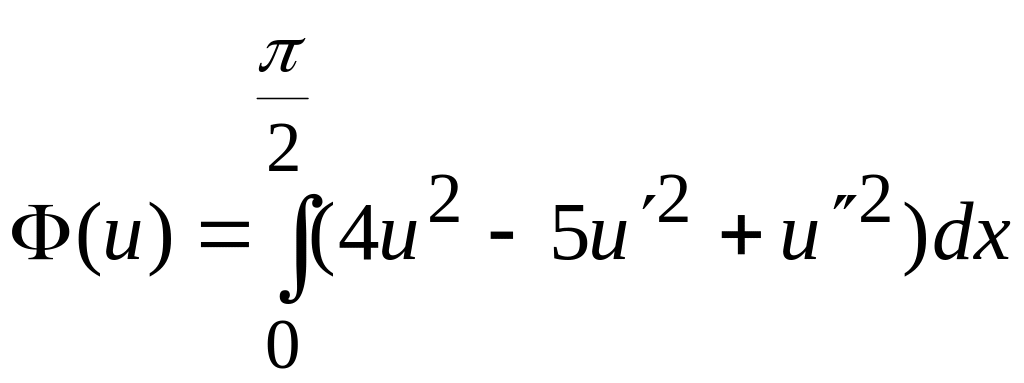
Задачи.

З.7.1. Получите необходимое условие экстремума для функционала (7.1) без условий (7.2) на правом конце.

З.7.2. Получите необходимое условие экстремума для функционала (7.1) без части условий на правом конце.

З.7.3. Сформулируйте аналог задачи Больца, получите необходимое условие экстремума.