
- •Математический анализ.
- •Часть 2
- •Введение
- •Программа курса высшей математики (математический анализ)
- •Неопределенный интеграл. Непосредственное интегрирование.
- •Задачи:
- •Замена переменной в неопределенном интеграле
- •Задачи:
- •Интегрирование по частям
- •Задачи:
- •Простейшие интегралы, содержащие квадратный трехчлен
- •Задачи:
- •Метод неопределенных коэффициентов
- •Задачи:
- •Интегрирование некоторых иррациональных функций
- •Задачи:
- •Интегралы от тригонометрических функций
- •Задачи:
- •Определенный интеграл. Формула Ньютона-Лейбница
- •Задачи:
- •Замена переменной в определенном интеграле
- •Задачи:
- •Несобственные интегралы
- •Задачи:
- •Индивидуальные семестровые задания
- •Литература
Метод неопределенных коэффициентов
ЛИТЕРАТУРА: [6] п. 24.3 – 24.4
Метод
неопределенных коэффициентов используется
для вычисления интегралов от рациональных
дробей вида
![]() многочлены степени m
и n
соответственно.
многочлены степени m
и n
соответственно.
Рассмотрим основные этапы нахождения интегралов данным методом.
1).
Если дробь
![]() неправильная, т.е. m
> n,
то необходимо выделить целую часть,
представив
в виде
неправильная, т.е. m
> n,
то необходимо выделить целую часть,
представив
в виде
![]() где
где
![]() - многочлены и степень многочлена
- многочлены и степень многочлена
![]() меньше n.
меньше n.
2).
Раскладываем знаменатель
![]() на множители:
на множители:
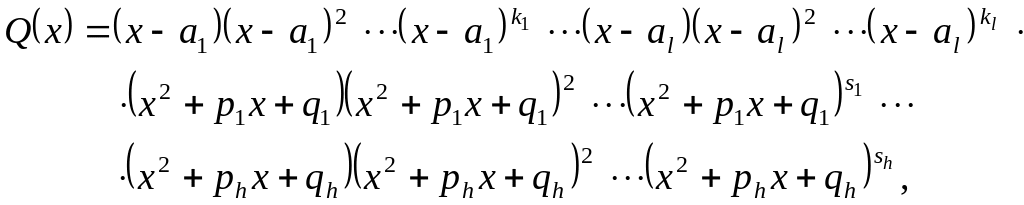
где
![]() являются
корнями многочлена
кратности
являются
корнями многочлена
кратности
![]() соответственно, а квадратные трехчлены
соответственно, а квадратные трехчлены
![]() не раскладываются на множители.
не раскладываются на множители.
3).
Дробь
![]() записывается как сумма элементарных
дробей:
записывается как сумма элементарных
дробей:
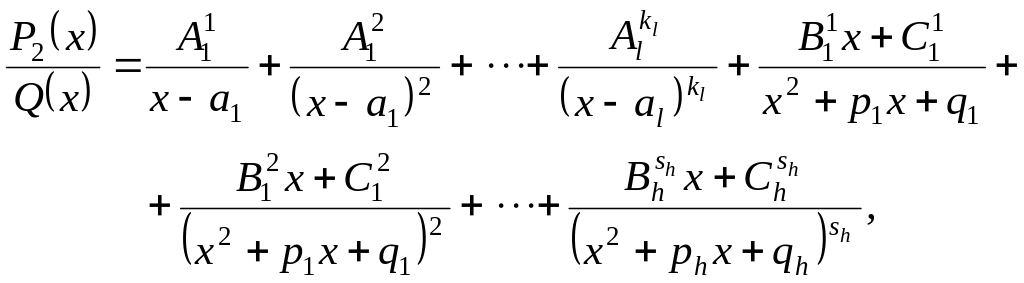
где
коэффициенты
![]() не
определены.
не
определены.
Пример
1.
Найти
![]()
Решение.
Так как степени многочленов
![]() равны, выделим целую часть:
равны, выделим целую часть:
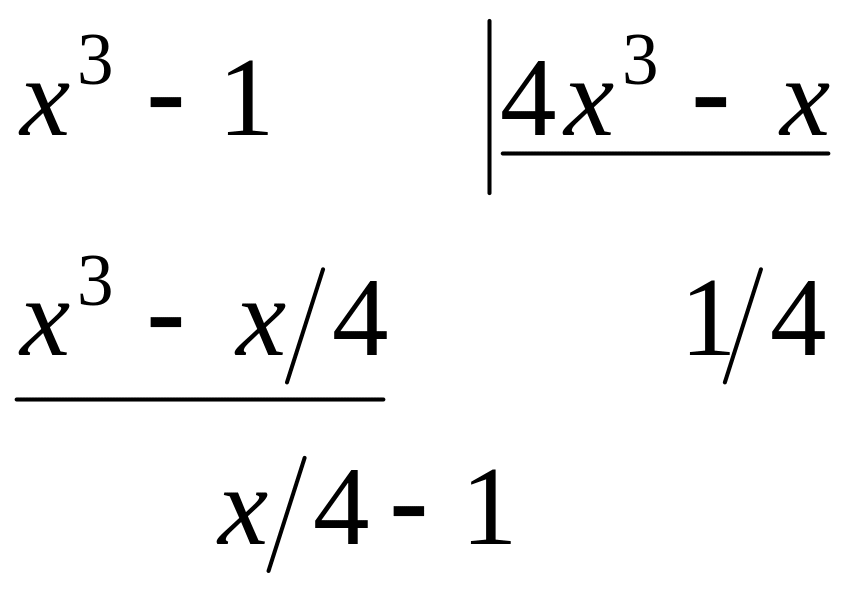
Получим:
![]() - целая часть,
- целая часть,
![]() - числитель дробной части. Т.е.
- числитель дробной части. Т.е.
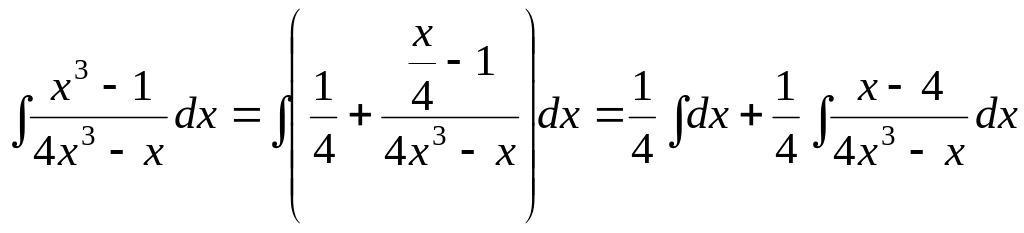
Разложим
знаменатель
![]() на множители:
на множители:
![]()
![]()
тогда
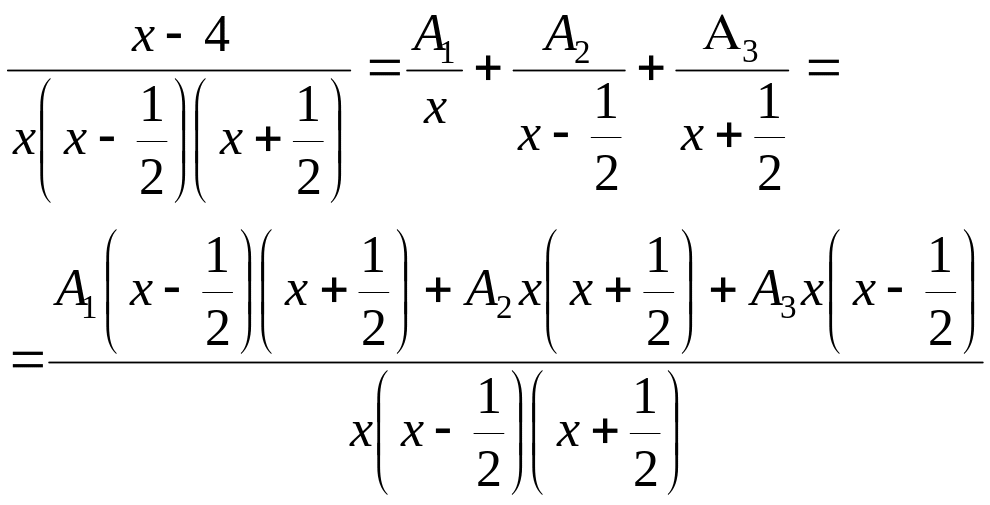
Приравниваем числители левой и правой дробей:
![]()
Пусть
![]()
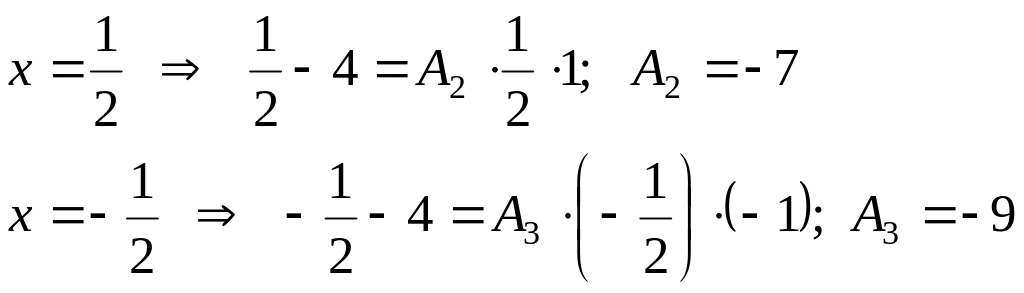
Подставляя найденные значения в разложение на элементарные дроби, получим:
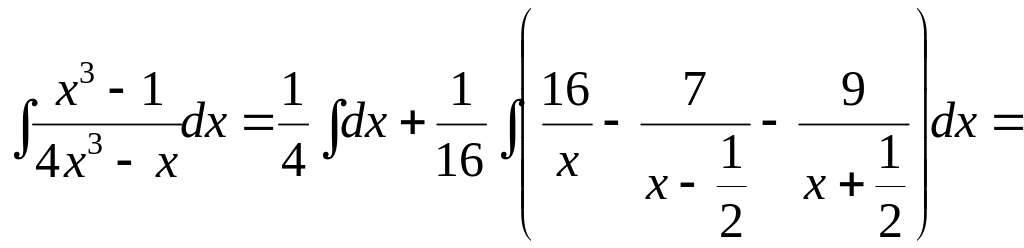
![]()
![]()
Пример
2.
Найти
![]()
Решение. Выделяем целую часть:
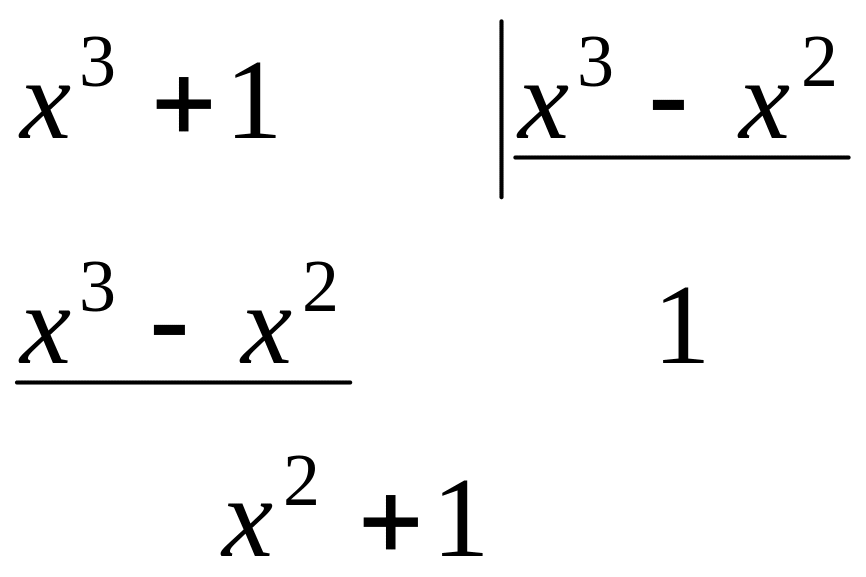
Следовательно:
![]()
![]() так
как корень x=0
кратности 2, то получим следующее
разложение на сумму дробей:
так
как корень x=0
кратности 2, то получим следующее
разложение на сумму дробей:
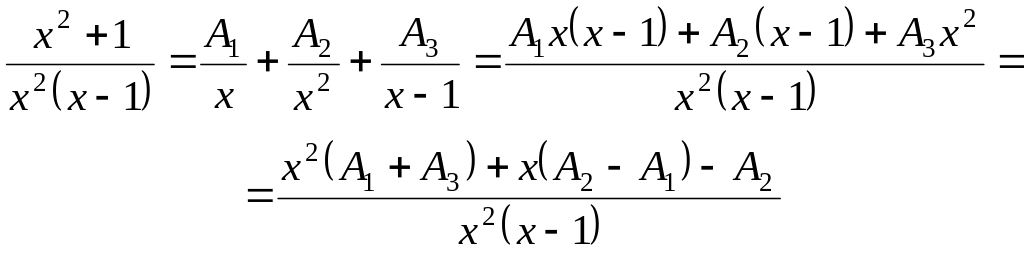
![]() и
получаем систему для нахождения
и
получаем систему для нахождения
![]()
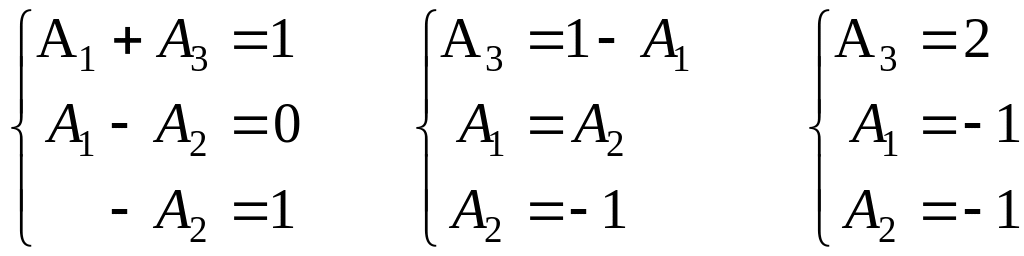
![]()
![]()
Задачи:
Найти интегралы:
1).
|
2).
|
3).
|
4).
|
5).
|
6).
|
7).
|
8).
|
9). |
10). |
Интегрирование некоторых иррациональных функций
ЛИТЕРАТУРА: [6] п. 25.3 – 25.5
1). Интегралы вида
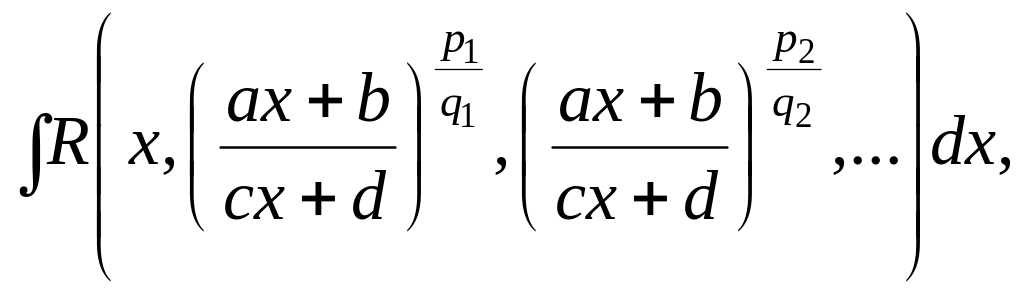 где
где
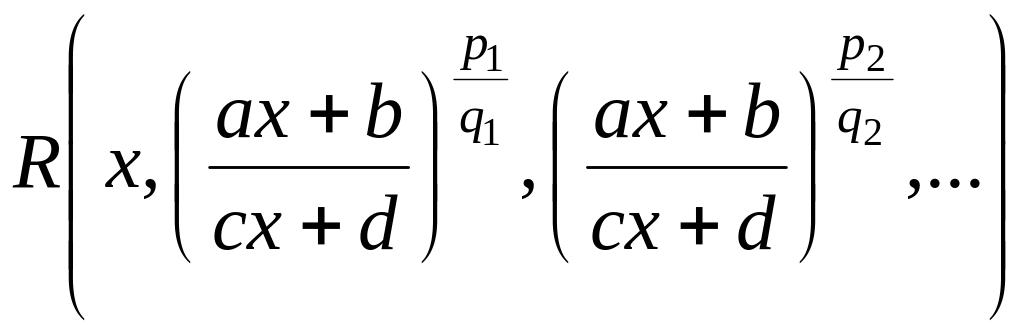 - рациональная функция своих аргументов;
- рациональная функция своих аргументов;
![]() -
целые числа, вычисляются с помощью
подстановки
-
целые числа, вычисляются с помощью
подстановки
![]() где s
– наименьший общий знаменатель дробей
где s
– наименьший общий знаменатель дробей
![]()
В
частности, для вычисления
![]() применяется подстановка
применяется подстановка
![]() где s
– наименьший общий знаменатель дробей
где s
– наименьший общий знаменатель дробей
Пример
1.
Найти
![]() .
.
Решение.
Делаем подстановку
![]() тогда
тогда
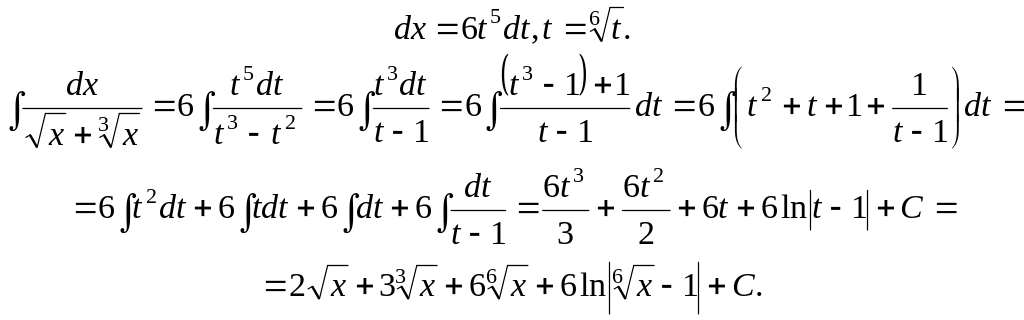
Пример
2.
Найти интеграл
![]()
Решение.
Делаем
подстановку
![]() тогда
тогда
![]() .
.
![]()
Методом неопределенных коэффициентов получаем
![]()
![]()
![]()
2).
Интеграл от дифференциального бинома
![]() где m,
n,
p
- рациональные
числа, может быть приведен к интегралу
от рациональных функций лишь в следующих
трех случаях (теорема Чебышева):
где m,
n,
p
- рациональные
числа, может быть приведен к интегралу
от рациональных функций лишь в следующих
трех случаях (теорема Чебышева):
а)
p
– целое число. Полагаем
![]() где N
– общий знаменатель дробей m
и n.
где N
– общий знаменатель дробей m
и n.
б)
![]() целое.
Полагаем
целое.
Полагаем
![]() где N
– знаменатель дроби p.
где N
– знаменатель дроби p.
в)
![]() целое.
Применяем подстановку
целое.
Применяем подстановку
![]() где N
– знаменатель дроби p.
где N
– знаменатель дроби p.
Если n = 1, то эти случаи эквивалентны следующим:
1) p – целое;
2) m – целое;
3) (m + p) – целое.
Пример
3. Найти
интеграл
![]()
Решение.
В нашем случае
![]() Так как p
– целое (случай а), то полагаем
Так как p
– целое (случай а), то полагаем
![]() тогда
тогда
![]() и интеграл примет вид:
и интеграл примет вид:
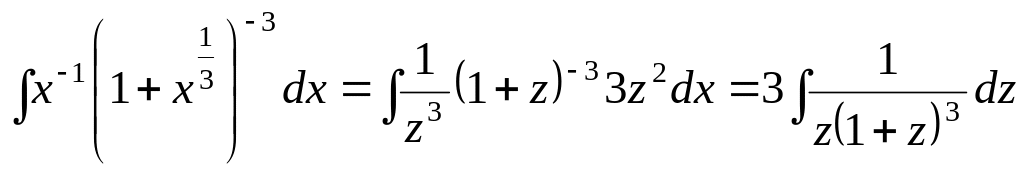
Для дальнейшего нахождения интеграла используем метод неопределенных коэффициентов
![]()
![]() т.е.
т.е.
![]()
Пусть
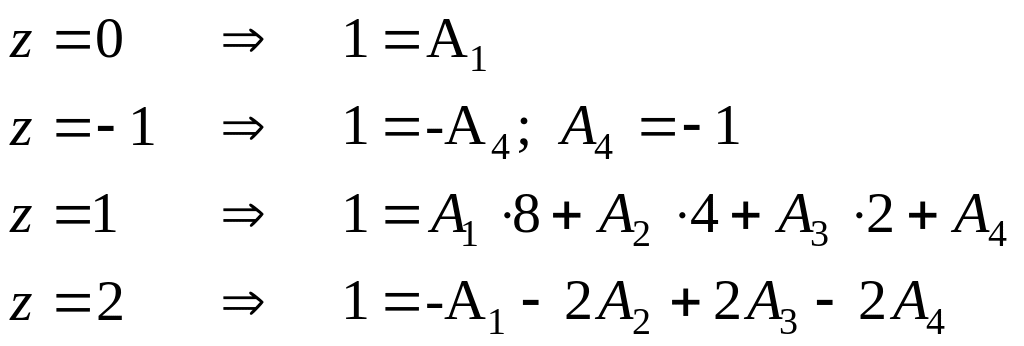
![]()
![]()
Тогда
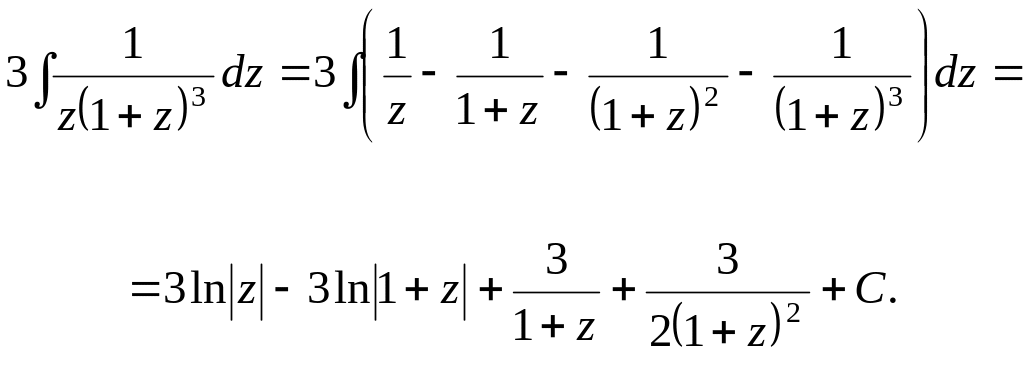
Подставляя
![]() получим окончательный ответ:
получим окончательный ответ:
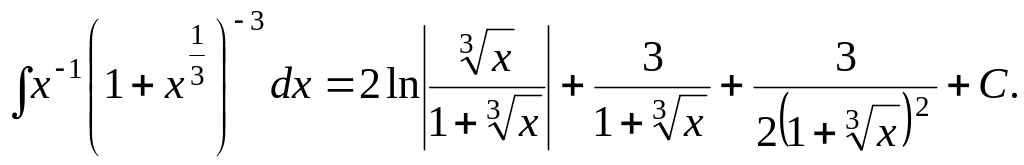
3).
Для интегралов вида
![]()
можно использовать подстановки Эйлера:
1).
Если a
> 0, то
![]()
2).
Если с
> 0, то
![]()
3).Если
![]() и
и
![]() - действительные корни трехчлена
- действительные корни трехчлена
![]() то
то
![]()
Пример
4. Найти
интеграл
![]()
Решение. В нашем случае а = 1 > 0, используем подстановку :
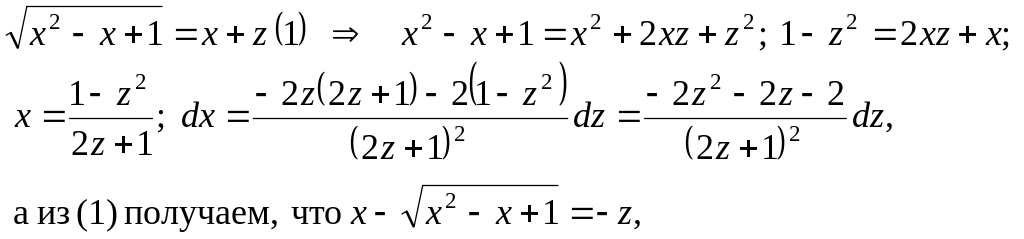
тогда интеграл
![]()
Для дальнейшего решения используем метод неопределенных коэффициентов.
