Розв’язання.

1. Знайдемо похідну .

2. Знаходимо критичні точки Інших точок немає .

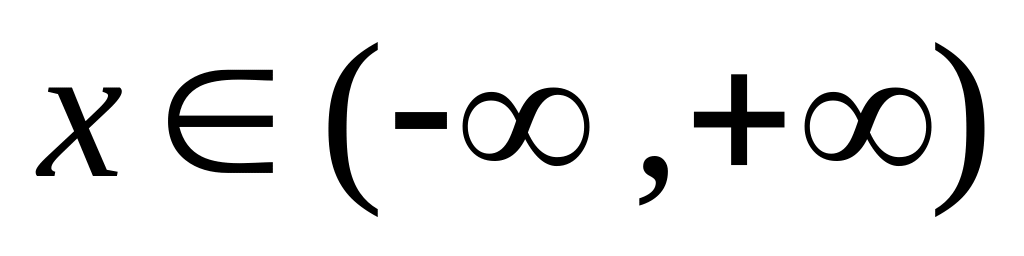3. Результати обчислень заносимо в табл. 1.

Таблиця 1

x		1	(1, 2)	2
	+	0	–	0	+
F(x)				min

4. Знаходимо:

.

.

Графік досліджуваної функції подано на рис. 7.

Друга достатня умова екстремуму: якщо перша похідна два рази диференційовної функції дорівнює нулю в деякій точці , а друга похідна в цій точці додатна, то х₀ є точкою мінімуму функції f(x); якщо від’ємна, то х₀ – точка максимуму.

Доведення. Нехай а Це означає, що також в деякому околі точки , тобто – зростаюча на (а;b), який містить точку . З умови зростання випливає, що на (а; ) і на ( ;b). Але Це означає, що на , а на – . Тобто при переході через похідна змінює знак з мінуса на плюс, а отже – точка мінімуму.

5.5. Найбільше та найменше значення функції на відрізку

Функція, неперервна на відрізку досягає на цьому відрізку свого найбільшого та найменшого значень. Ці значення вона може досягати на одному з кінців відрізку, або всередині відрізка.

Тому для знаходження найбільшого та найменшого значень функції на треба:

1. знайти всі критичні точки;

2. знайти значення функції на кінцях відрізка та в критичних точках, що належать відрізку;

3. із одержаних значень вибрати найменше та найбільше.

5.6. Опуклість та угнутість графіка функції. Точки перегину

Означення. Крива називається опуклою (угнутою) на інтервалі , якщо усі точки графіка функції лежать нижче (вище) точок її дотичних на цьому інтервалі.

Теорема. Якщо в усіх точках інтервалу друга похідна то крива є угнутою на цьому інтервалі; якщо на інтервалі то крива опукла на цьому інтервалі.

Означення. Точкою перегину графіка неперервної функції називається точка, яка розділяє інтервали, в яких функція опукла і угнута.

Правило. Точка x=x₀ буде точкою перегину кривої , якщо:

1. або не існує;

2. знаки зліва (x<x₀) та справа (x>x₀) різні.

5.7. Асимптоти графіка функції

Означення. Пряму лінію називають асимптотою кривої , якщо відстань точки М кривої від цієї прямої прямує до нуля при віддалені точки М в нескінченість.

Асимптоти бувають вертикальні, горизонтальні та похилі.

Пряма є вертикальною асимптотою, якщо хоча б одна із границь або Якщо лише або , то функція має лише односторонню асимптоту.

Пряма є горизонтальною асимптотою, якщо .

Рівняння похилої асимптоти будемо шукати у вигляді , де a і b деякі коефіцієнти.

Виходячи з означення асимптоти можемо записати (d – відстань від прямої до асимптоти)

З останнього випливає

. Звідси .

Якщо існує скінчене то коефіцієнт b знаходиться за допомогою границі

Приклад. Знайти асимптоти кривої . Асимптоту будемо шукати у вигляді , де

, .

Таким чином асимптотою є пряма .

Знайдемо екстремальні точки. Знаходимо похідну і прирівнюємо її до нуля

Рис. 8

.

Знаходимо розв’язок рівняння:   . Точка є екстремальною точкою.

Дослідимо знак другої похідної в екстремальній точці: . Поклавши , одержимо, що , а отже, в точці функція має мінімум (див. рис. 8).

Загальна схема дослідження функцій і побудова їх графіків

1. Знайти область визначення функції.

2. Дослідити функцію на парність-непарність.

3. Знайти вертикальні асимптоти.

4. Дослідити поведінки функції на нескінченності, знайти горизонтальні та нахилені асимптоти.

5. Знайти екстремуми і інтервали монотонності функції.

6. Знайти інтервали опуклості та угнутості і точки перетину.

7. Знайти точки перетину з осями координат і, можливо, деякі додаткові точки, які уточнюють графік функції.

Приклад 1. Дослідити функцію та побудувати її графік.

1. Область визначення. Розрив у точці . Отже .

2. Перевірка парності. . Це означає, що дана функція не буде ні парною, а ні непарною.

3. Знайдемо вертикальні асимптоти: . Це означає, що дана функція має вертикальну асимптоту .

4. Знайдемо нахилені та горизонтальні асимптоти :

,

Отже – горизонтальна асимптота.

5. Знайдемо екстремуми:

.

Звідси а отже – точка екстремуму.

Результати досліджень зведено в табл. 2

Таблиця 2

x		0	(0;1)	1
	–	0	+	не існує	–
f(x)				не існує

Рис.9.

Таким чином задана функція на інтервалі – зростає, а на інтервалах і – спадає. В точці приймає мінімальне значення

6. Знайдемо інтервали опуклості, угнутості і точки перегину за допомогою другої похідної:

.

З умови рівності другої похідної нулю знаходимо:  . З нижче наведеної табл. 3 видно, що ця точка є точкою перегину. Графік досліджуваної функції наведено на рис. 9.

Таблиця 3

x				1
	–	0	+	не існує	+
f(x)		точка перегину		не існує

Приклад 2. Дослідити та побудувати графік функції , яка називається логістичною кривою. В економіці її використовують для визначення тенденції росту виробництва предметів споживання. Дослідження провести при .

Рис. 10

Розв’язання:

1. область визначення функції: уся дійсна числова вісь;

2. точки розриву відсутні;

3. в ертикальні асимптоти відсутні, але є горизонтальні вигляду :

ln2

, ,

, .

Таким чином крива має дві горизонтальні асимптоти: – правостороння і – лівосто­рон­ня;

4. точки перетину з віссю абсцис відсутні, функція додатна для всіх х;

5. похідна для всіх х, це означає, що функція зростаюча у всій області, а отже не має екстремумів;

6. друга похідна при 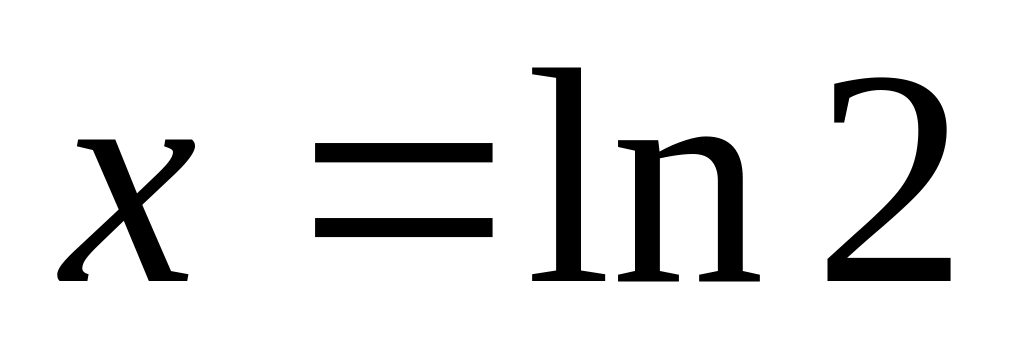, це означає, що точка з координатами є точкою перегину, оскільки друга похідна міняє знак при переході через точку з абсцисою ;

7. точка перетину графіка функції з віссю ординат: ;

8. графік функції подано на рис. 10.