5.3. Зростання та спадання функції. Основні теореми

Рис. 3

Означення. Функцію називають зростаючою (спадною) на проміжку ( ), якщо більшому значенню аргументу в цьому проміжку відповідає більше (менше) значення функції, тобто якщо із нерівності випливає нерівність , то функція – зростаюча, а якщо , то функція спадна.

На рис. 3 бачимо, що на проміжку ( ) функція – зростаюча, а – спадна.

Теорема 1 (достатня ознака зростання (спадання) функції). Якщо похідна диференційовної функції додатна (від’ємна) всередині деякого проміжку, то функція зростаюча (спадна) на цьому проміжку.

Доведення. Нехай при . Для довільних , що належать ( ), згідно з теоремою Лагранжа, маємо

,

де , а тому . Із нерівностей та випливає, що або при . А це означає, що функція зростаюча.

Аналогічно доводиться теорема для спадної функції.

Теорема 2 (необхідна умова зростання (спадання) функції). Якщо диференційовна функція зростає (спадає) в деякому проміжку, то похідна цієї функції невід’ємна (не додатна) в цьому проміжку.

Доведення. Нехай – диференційовна функція і зростає на ( ). Згідно з означенням похідної

.

Якщо та належать ( ), то в силу зростання функції знаки приросту функції та приросту аргументу однакові

, при .

Оскільки границя додатної величини не може бути від’ємною, тому переходом до границі в цій нерівності одержимо . Це і доводить теорему.

У випадку спадної функції доведення аналогічне. У цьому випадку прирости функції і прирости аргумент мають різні знаки, тому

, при і .

Означення. Зростаюча або спадна функція називається монотонною. Інтервали, на яких задана функція зростає або спадає називаються інтервалами монотонності.

Для знаходження інтервалів монотонності заданої функції доцільно дотримуватись такого правила:

1. знайти ;

2. знайти корені рівняння ;

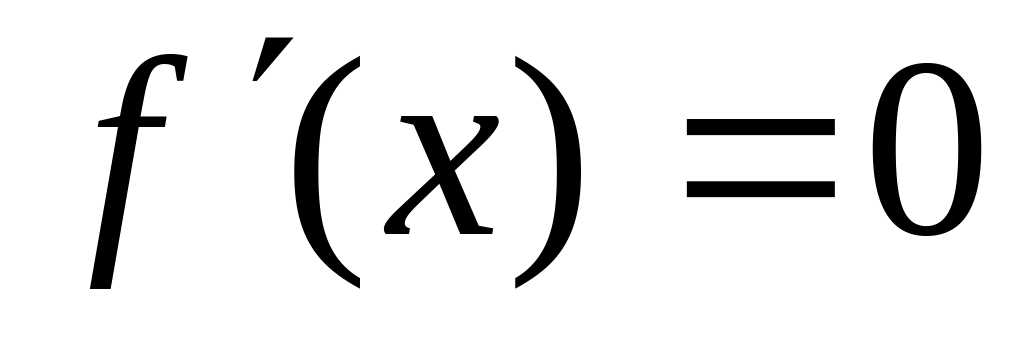3. визначити знак похідної в кожному із інтервалів, на які поділяється область існування функції знайденими коренями рівняння ;

4. за одержаними знаками похідної зробити висновки, в яких інтервалах функція зростає, а в яких спадає.

Приклад. Витрати виробництва визначаються функцією . Знайти її інтервали монотонності.

Розв’язання. Задана функція визначена при , але має економічний зміст лише при .

1. Знайдемо похідні: .

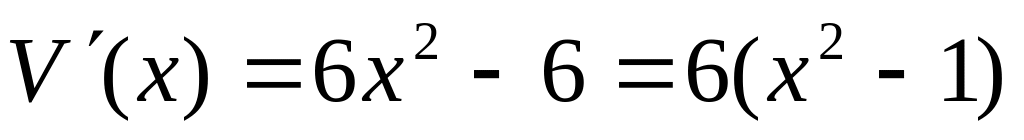2. Знайдемо корені рівняння : .

Ці значення поділяють область визначення на інтервали , і . В кожному з цих інтервалів має постійний знак:

при ,

при ,

при .

Отже функція зростає в інтервалах і , а спадає на інтервалі . З економічної точки зору ця функція спадає на інтервалі і зростає на інтервалі .

5.4. Екстремуми функції. Необхідна і достатні умови екстремуму

Означення. Точка називається точкою локального максимуму (мінімуму) функції , якщо в деякому околі точки виконується нерівність – для максимуму ( – для мінімуму).

Рис. 4

Узагальненим терміном поняття максимуму та мінімуму є екстремум. Значення аргументу (тобто точка ), при якому функція має екстремум (максимум чи мінімум) називають точкою екстремуму функції.

Зауважимо, що екстремальні точки, згідно з означенням, це такі точки, в яких функція набуває відповідно найбільшого чи найменшого значень порівняно із значеннями функції, що їх вона набуває в точках, досить близьких до екстремальної точки. Такий екстремум функції часто називають локальним (від лат. lokalis, що означає “місцевий”).

Окремий локальний мінімум може бути більший за окремий локальний максимум, як це видно, наприклад, з рис. 4. Функція, графік якої зображено на цьому рисунку, в точці має мінімум, більший за максимум, який набуває в точці .

Необхідна умова екстремуму. Якщо в точці диференційовна функція має екстремум, то в деякому околі цієї точки виконуються умови теореми Ферма, а це значить, що похідна в цій точці дорівнює нулю, тобто . Але функція може мати екстремум і в точках, в яких вона не диференційовна. Так, наприклад, функція має екстремум (мінімум) в точці , але не диференційовна в цій точці. А функція також має в точці мінімум (див. рис. 5), а похідна її в цій точці нескінченна:

Д

Рис. 5

ійсно,

Звідки одержуємо, що .

Тому необхідна умова екстремуму може бути сформульована наступним чином:

Для того, щоб функція мала екстремум в точці , необхідно, щоб її похідна в цій точці дорівнювала нулю ( ) або не існувала.

Точки, в яких виконана необхідна умова екстремуму, тобто похідна дорівнює нулю або не існує, називаються критичними (або стаціонарними).

Обернене твердження невірне.

Рис. 6,б

Рис.6,а

Рис. 6,в

Приклад. Знайти критичні точки функції і переконатися в наявності або відсутності екстремуму в цих точках:

, . – критична точка (точка мінімуму) (Рис. 6,а).

, . – критична точка (екстремум відсутній) (Рис. 4,б).

3) , , . – критична точка (екстремум відсутній) (Рис. 6,б).

П ерша достатня умова екстремуму: Якщо при переході через точку похідна диференційовної функції міняє свій знак з плюса на мінус, то точка є точкою максимуму функції , а якщо з мінуса на плюс – то точкою мінімуму.

Схема дослідження функції на екстремум

1. Знайти похідну .

2. Знайти критичні точки функції, в яких похідна дорівнює нулю або не існує.

3. Дослідити знак похідної зліва і справа від кожної критичної точки і зробити висновок про наявність екстремуму.

4. Знайти екстремуми.

Приклад. Знайти екстремуми функції .