3.Нелинейное программирование

3.1. Экстремумы в многомерных задачах

Пусть n-мерный вектор, а F(x) – дважды непрерывно дифференцируемая функция переменной x , т.е. F(x) функция n переменных x_i. Обозначим градиент¹ F(x) в точке x₀ = т.е. это n-мерный вектор-столбец, координатами которого являются частные производные F(x) по координатам x_i, вычисленные в некоторой точке x₀. Как известно, первый дифференциал представляется в виде скалярного произведения вектора-градиента на вектор смещения dx.

dF(x₀) = dx₁ + dx₂ + …+ dx_n = ( dx)

3.1.2 Матрицца Гессе (гессиан)

Для того, чтобы в векторной форме записать второй дифференциал нам понадобится построить специальную матрицу. Вычислив градиенты каждой из координат вектора-градиента , мы получим n векторов, каждый из которых содержит n координат, равных вторым частным производным функции F(x). Расположив координаты этих n векторов по столбцам матрицы, мы получим квадратную n-мерную матрицу; такая матрица называется матрицей Гессе или гессианом функции F(x):

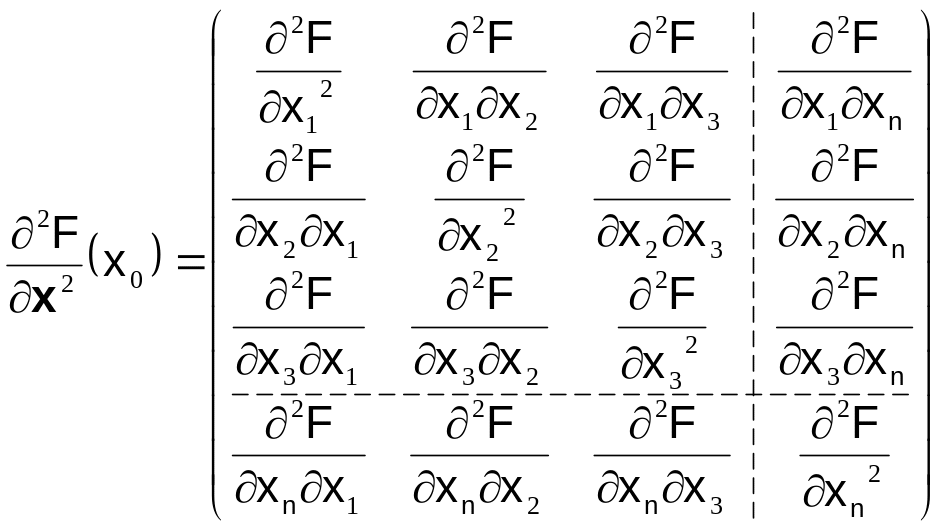
Т.к. , то гессиан всегда симметричная матрица, и, следовательно, может порождать квадратичную форму. Второй дифференциал d²F представляет собой сумму произведений вторых частных производных на произведение соответствующих приращений независимых переменных:

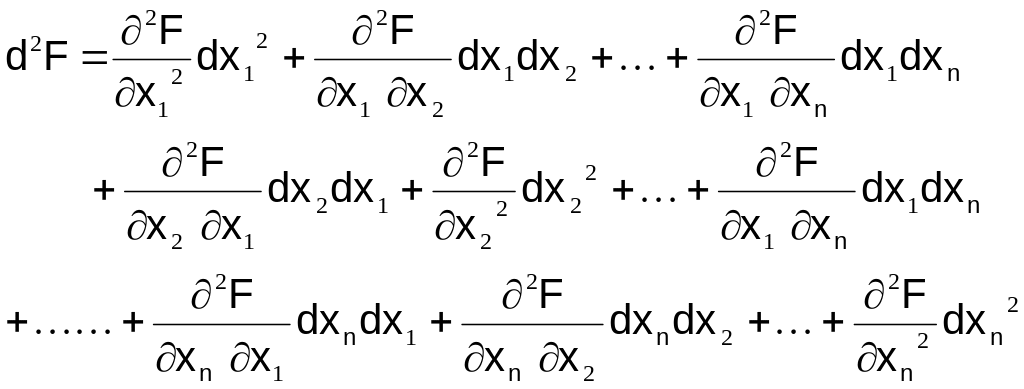
Легко видеть, что перед нами квадратичная форма относительно приращений переменных dx₁, dx₂, dx₃, … dx_n, коэффициенты которой совпадают с элементами матрицы Гессе (гессиана). d²F(x₀) = (dx dx)

Здесь dx=(dх₁, dх₂, dх₃,... dх_n) – вектор-строка, а dx – соответствующий вектор-столбец, круглые скобки означают скалярное (матричное) произведение. При введенных обозначениях выражение для приращения дважды непрерывно дифференцируемой функции двух переменных выглядит абсолютно так же, как и для приращения функции одной переменной и может рассматриваться как приращение функции одной векторной переменной

F=F(x₀+x)– F(x₀)=

3.1.3 Необходимые и достаточные условия экстремума

Вполне аналогично случаю одной переменной необходимым условием экстремума является тождественное равенство нулю первого дифференциала, что эквивалентно требованию равенства градиента нуль-вектору = 0 . Точки, в которых это условие выполнено, называются, как и в случае одной переменной, стационарными.

Достаточное условие наличия экстремума формулируется так же, как и в случае одной переменной: для наличия экстремума в стационарной точке достаточна знакоопределенность второго дифференциала, причем положительная определенность достаточна для минимума, а отрицательная определенность  для максимума:

d²F(x₀) = (dx dx) > 0  min

d²F(x₀) = (dx dx) < 0  max

По критерию Сильвестра для положительной определенности квадратичной формы необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительны, а для отрицательной определенности квадратичной формы необходимо и достаточно, чтобы знаки главных миноров чередовались, т.е. чтобы у минора i-го порядка был знак (–1)ⁱ. Таким образом, критерий Сильвестра, примененный к гессиану, дает нам инструмент для выяснения вопроса о наличии экстремума в стационарной точке функции нескольких переменных.