
- •Принятые обозначения
- •1. Множества
- •1.1. Операции над множествами
- •1.2. Отображения
- •2. Линейные пространства
- •2.1. Примеры линейных пространств
- •2.2 Размерность, базис, координаты
- •2.2.1 Линейная комбинация и разложение по набору
- •2.2.2 Линейная зависимость
- •2.2.3. Некоторые замечания
- •2.2.4. Размерность и базис
- •2.3. Примеры
- •2.4. Изоморфизм линейных пространств
- •2.5. Подпространства
- •2.6. Примеры подпространств
- •3. Матрицы и определители
- •3.1. Действия над матрицами
- •3.2. Определители
- •3.3. Свойства определителей
- •3.4. Примеры
- •3.5. Обратная матрица
- •3.6. Ранг прямоугольной матрицы
- •4. Линейные операторы
- •4.1. Действия над операторами
- •4.2. Примеры линейных операторов
- •4.3. Линейные уравнения
- •4.4. Матрица линейного оператора
- •4.5. Примеры
- •4.6. Переход к новому базису
- •4.7. Собственные значения и собственные векторы линейного оператора
- •5. Системы линейных уравнений
- •5.1. Случай квадратной матрицы (система порядка n n)
- •5.1.1. Метод обратной матрицы
- •5.1.2. Правило крамера
- •5.1.3. Пример
- •5.2. Метод гаусса. Случай невырожденной квадратной матрицы
- •5.2.1. Прямой ход метода гаусса
- •5.2.2. Обратный ход
- •5.3. Случай прямоугольной матрицы (системы порядка m n)
- •5.3.1. Прямой ход
- •5.3.2. Обратный ход
- •5.4. Пример решения неопределенной системы
- •5.5. Определение ранга матрицы
- •5.6. Нахождение собственных векторов
- •6. Евклидовы пространства и элементы аналитической геометрии
- •6.1. Базисы в евклидовом пространстве
- •6.2. Точки в евклидовом пространстве
- •6.2.1. Сферы и шары
- •6.2.2. Замечание о размерностях
- •6.3. Плоскости в пространстве
- •6.3.1. Неединственность выбора параметров. Каноническая форма уравнения плоскости
- •6.3.2. Геометрический смысл параметров уравнения плоскости
- •6.3.3. Плоскости и линейные функционалы75
- •6.3.4. Сводка формул: плоскость
- •6.4. Прямые в пространстве
- •6.4.1. Геометрический смысл параметров уравнения прямой
- •6.4.2. Прямая, проходящая через две заданные точки
- •6.4.3. Сводка формул: прямая в пространстве
- •6.5. Прямые на плоскости
- •6.6. Векторное и смешанное произведение. Площади и объемы
- •6.6.1. Смешанное произведение и вычисление объемов
- •6.7. Квадратичные формы
- •6.8. Задачи и решения
- •6.8.1. Плоскости и прямые
- •6.8.2. Векторы, длины, объемы
- •6.8.2. Квадратичные формы
5.3.2. Обратный ход
Обратный ход для неопределенных систем имеет существенные особенности. Как известно из общей теории линейных операторов58, в этом случае необходимо построить общее решение системы, которое представляет собой сумму некоторого частного решения неоднородной системы (15) и общего решения соответствующей однородной системы, т. е. системы с той же матрицей и правыми частями, равными 0:
![]() (15.1)
(15.1)
Для решения этой задачи после исключения зависимых строк перенесем все столбцы с номерами больше, чем k (т. е. все столбцы, не входящие в базисный минор), в правую часть:
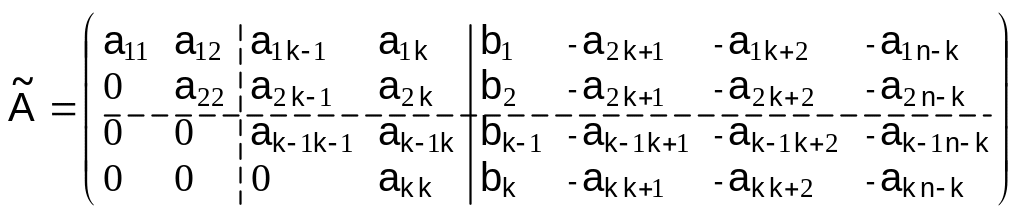 . (23)
. (23)
Частное решение неоднородной системы (15) проще всего найти, положив в (23) xk+1 = xk+2 = xk+3 …. = xn-k = 0. В результате получим совместную определенную систему из k уравнений:
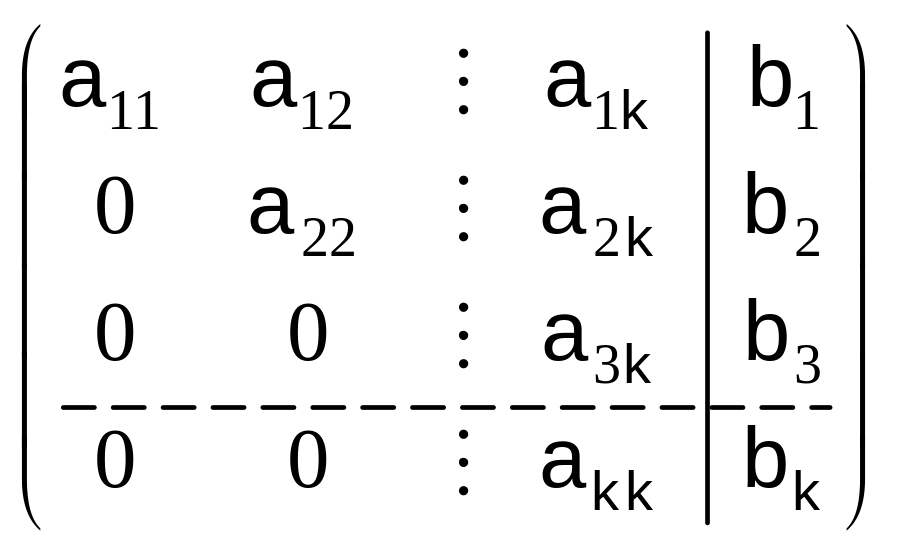 .
.
Поскольку она уже приведена к треугольному виду, осталось выполнить обратный ход процедуры Гаусса, чтобы вычислить первые k координат частного решения x0, а последние n – k координат равны 0.
Таким образом, мы найдем частное решение неоднородной системы уравнений. Общее решение однородной системы (15.1) также найдем из системы (23)59. Т. к. ранг системы равен k, а число неизвестных равно n, то размерность ядра матрицы равна n – k; значит общее решение однородного уравнения должно содержать n – k независимых векторов. Мы найдем их, последовательно придавая переменным {xk+1, xk+2, xk+3, … xn} такие наборы значений
первый xk+1 = 1 xk+2 = 0 xk+3 = 0…. = xn = 0
второй xk+1 = 0 xk+2 = 1 xk+3 = 0…. = xn = 0
третий xk+1 = 0 xk+2 = 0 xk+3 = 1…. = xn = 0 (24)
………………………………………………………...........
последний, n – k -ый xk+1 = 0 xk+2 = 0 xk+3 = 0…. = xn = 1
Решая n – k раз систему (23) с перечисленными в (24) правыми частями, получим n – k независимых решений однородной системы (20), которые и образуют фундаментальную систему решений однородной системы (22)60.
5.4. Пример решения неопределенной системы
Рассмотрим систему уравнений
![]()
Расширенная матрица системы имеет вид
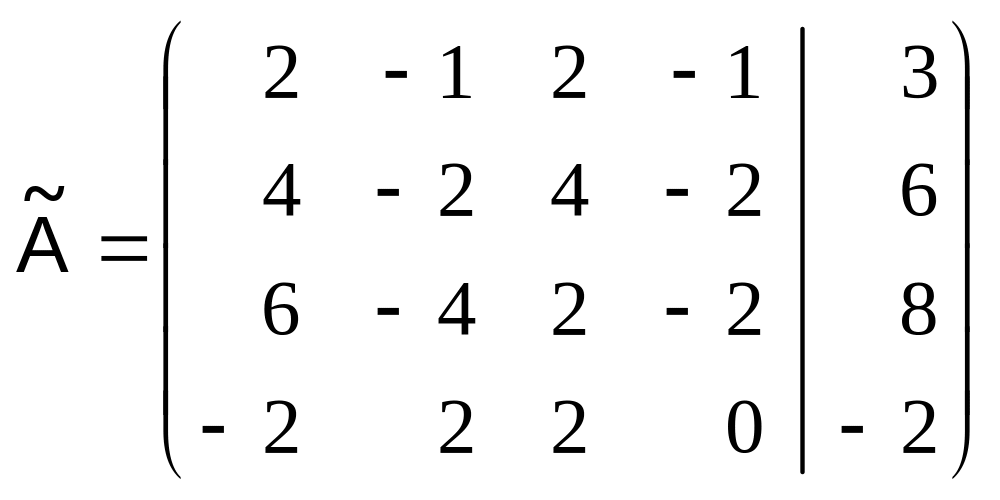 .
.
Теперь начнем процедуру Гаусса. Умножим в соответствии с (18) первую строку на – 2 и добавим ко второй; соответственно, умножаем первую строку на – 3 и добавляем к третьей, умножаем на 1 и добавляем к четвертой по-лучим:
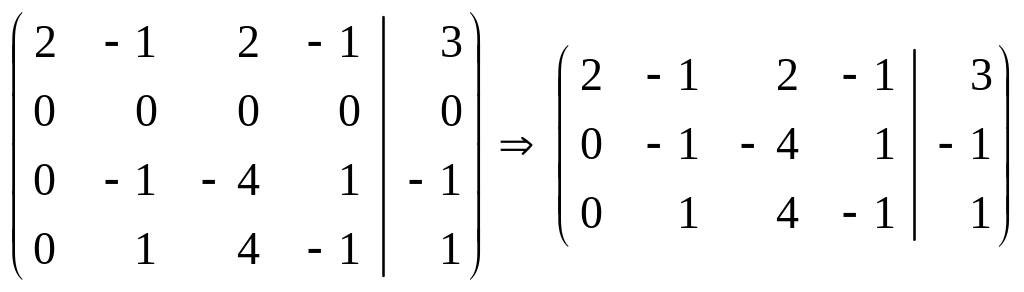 .
.
Мы получили вторую строку из одних нулей и, в соответствии с алгоритмом исключили вторую строку, а остальные строки сдвинули, получив матрицу 3 4. Теперь умножаем вторую строку на 1 и прибавляем к третьей
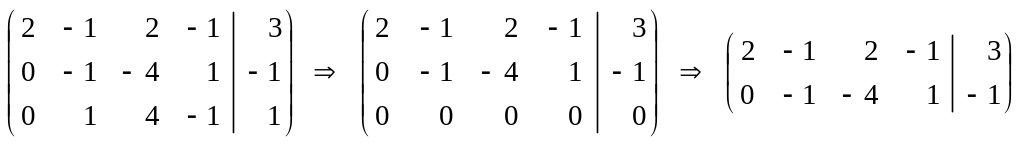 .
.
Исключив еще одну строку расширенной матрицы, состоящую из одних нулей, мы получили совместную неопределенную систему 2-х уравнений с 4-мя неизвестными. Это соответствует ситуации, изображенной формулой (21), – два левых столбца представляют собой треугольную матрицу второго порядка. Теперь, в соответствии с общим алгоритмом, третий и четвертый столбец перенесем в правую часть. Получим (см. (23))
![]() .
.
Для определения частного решения неоднородного уравнения, положим x3 = x4 = 0. Получим совместную определенную систему 2-х уравнений с двумя неизвестными, для решения которой достаточно проделать обратный ход процедуры Гаусса
![]() .
.
Из второго уравнения получим x2 = 1. Тогда из первого уравнения 2x1 = 3 – – (–11) = 4 x1 = 2. Таким образом, частное решение неоднородного уравнения: x0 = {2, 1, 0, 0} (здесь и далее мы векторы-столбцы найденных решений записываем в строку – по соображениям удобства).
Теперь, полагая bi = 0 и задавая неизвестным x3, x4 значения по схеме (24), найдем фундаментальную систему решений однородной системы (15.1)
x3 = 1; x4 = 0;
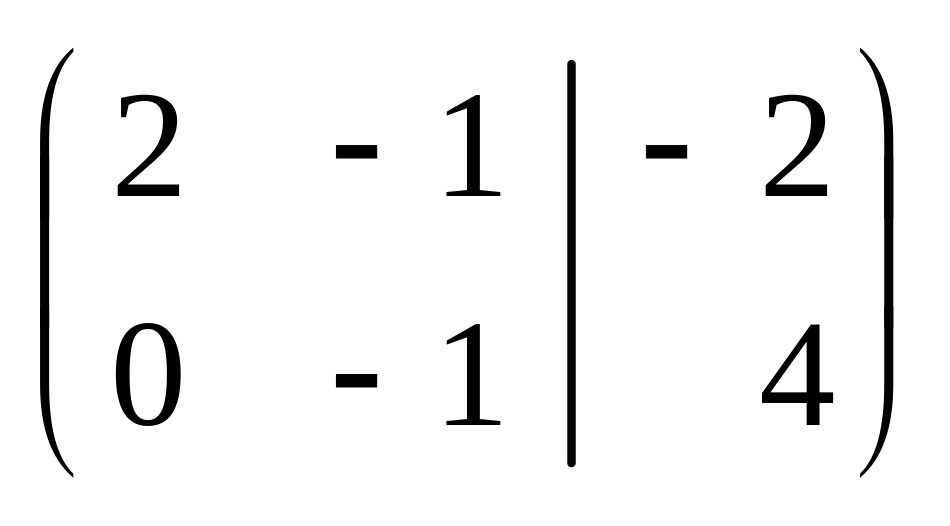
x2
= – 4;
x1
= 3.
x2
= – 4;
x1
= 3.x3 = 0; x4 = 1;
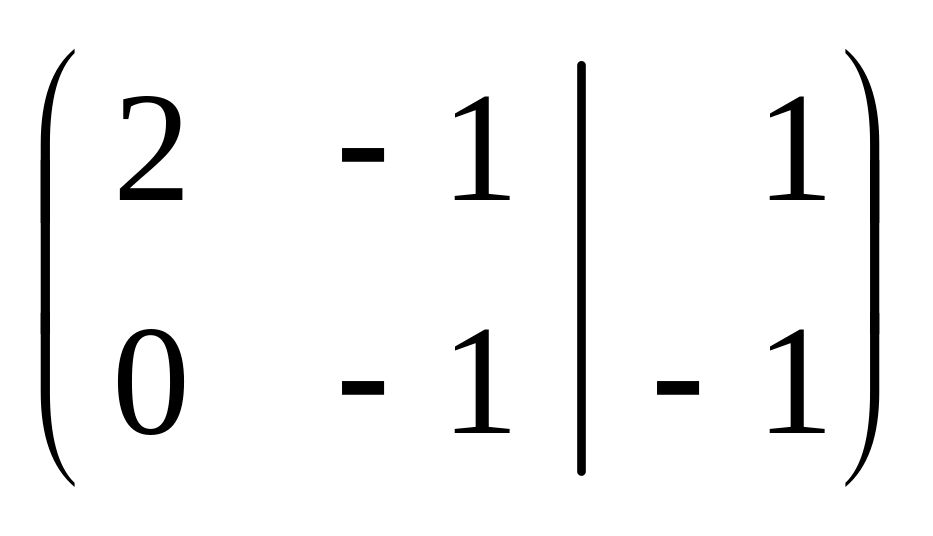
x2
= 1;
x1
= 1.
x2
= 1;
x1
= 1.
Таким образом, фундаментальную систему решений однородного уравнения образуют два решения: f1 = {– 3, – 4, 1, 0}, f2 = {1, 1, 0, 1}. Соответственно, общее решение неоднородного уравнения имеет вид:
 .
.
Здесь с1, с2 – произвольные константы.
