Питання для самоконтролю

1. Сформулюйте основні закони геометричної оптики.

2. У чому полягає явище повного внутрішнього відбивання світла?

3. Що називають лінзою, фокусом, фокусною відстанню, оптичною силою лінзи? Запишіть формулу тонкої лінзи.

4. Що називають лінійним збільшенням лінзи і як його визначають?

5. Побудуйте зображення для збиральної і розсіювальної лінз. (Розгляньте всі можливі випадки).

6. У чому полягає суть методу зміщення для визначення фокусної відстані збиральної лінзи?

7. Які особливості методу визначення фокусної відстані розсіювальної лінзи?

Лабораторна робота № 2 визначення довжини світлової хвилі методом кілець ньютона

Мета роботи: визначити довжину світлової хвилі червоного світла за допомогою кілець Ньютона.

Прилади та матеріали: оптична лава, джерело світла, конденсор, монохроматичний світлофільтр, плоско-опукла лінза великого радіуса кривини, скляна плоско-паралельна пластина, лінза.

Короткі теоретичні відомості

Окремим випадком смуг рівної товщини є кільця Ньютона, які утворюються внаслідок інтерференції світла у повітряному прошарку між плоскою скляною пластинкою і прикладеною до неї опуклою стороною плоско-опуклою лінзою великого радіуса кривини R (рис. 2.1).

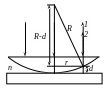
Рис. 2.1

При спостереженні інтерференційної картини у відбитому світлі в її центрі бачитимемо темний круг (оптичний контакт лінзи і пластинки), а навколо неї – чергування світлих і темних кілець, ширина яких поступово зменшується з віддаленням від центра. У прохідному світлі буде обернена картина – центральний світлий круг, наступне кільце темне, потім – світле і т.д.

Для утворення кілець Ньютона паралельний пучок монохроматичних світлових променів спрямовують нормально на плоску поверхню лінзи. Частина цього світлового пучка відбивається від опуклої поверхні лінзи на межі «скло – повітря» (промінь 1), а решта проходить повітряний прошарок між лінзою та пластинкою і відбивається від пластинки на межі «повітря - скло» (промінь 2). Відбиті світлові хвилі – когерентні, вони мають однакову частоту і сталу різницю фаз, яка виникає тому, що хвиля 2 проходить більший шлях, ніж хвиля 1. При їх накладанні виникають інтерференційні смуги. Оскільки результат накладання двох відбитих хвиль залежить від товщини повітряного прошарку d, то для всіх точок цього прошарку, що знаходяться на однаковій відстані r від точки дотику лінзи і пластинки, тобто тих, що утворюють кільце, буде однакова умова інтерференційного максимуму або мінімуму.

Оптична різниця ходу між променями 2 і 1 становить , де доданок враховує втрату півхвилі при відбиванні світла від оптично більш густого середовища (скла). У даному випадку кут падіння променів і показник заломлення повітря , тому рівняння набуває вигляду:

. (2.1)

Із прямокутного трикутника визначимо відстань d, скориставшись залежністю . Розкриємо дужки: . Беручи до уваги, що d << R, величиною d² нехтуємо, тоді , звідкіля маємо: . Підставимо отримане значення d у вираз (2.1), одержимо:

. (2.2)

Підставимо у вираз (2.2) умову максимуму інтерференції , отримаємо: .

Отже, радіус k-го світлого кільця Ньютона у відбитому світлі:

, де k =1,2,3…– номер кільця. (2.3)

Враховуючи умову мінімуму інтерференції: , можна одержати радіус k-го темного кільця Ньютона у відбитому світлі:

, де k =0,1,2,3…– номер кільця. (2.4)

У прохідному світлі втрати півхвилі немає, положення світлих і темних кілець міняються місцями, тому радіус k-го світлого кільця у прохідному світлі визначається за формулою (2.4), а темного кільця – за формулою (2.3).

Методом кілець Ньютона можна знайти довжину світлової хвилі. З виразу (2.3) або (2.4) знайдемо λ. Запишемо формули, наприклад, для m-го і k-го світлих кілець Ньютона у відбитому світлі:

і ,

та знайдемо їх різницю:

,

звідки

. (2.5)

За формулою (2.5) не можна відразу обчислити довжину хвилі, тому що лабораторна установка дає збільшене в  разів зображення кілець Ньютона на екрані, тому розрахункова формула:

. (2.6)

Радіус кривини лінзи у даній роботі R = 19,5 м.