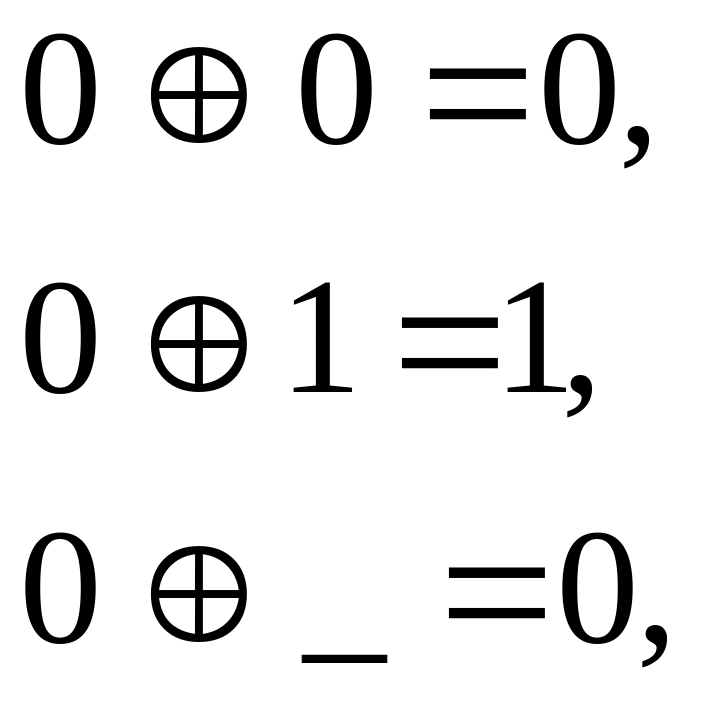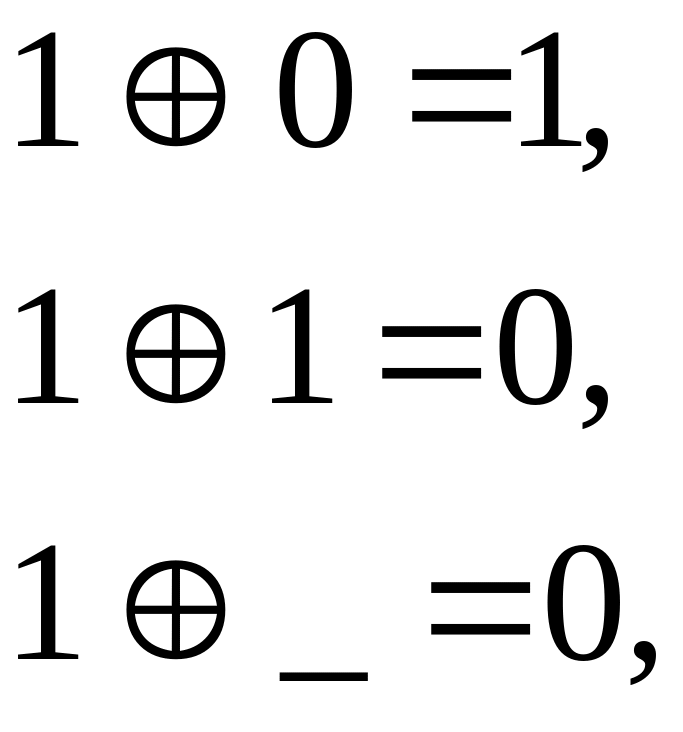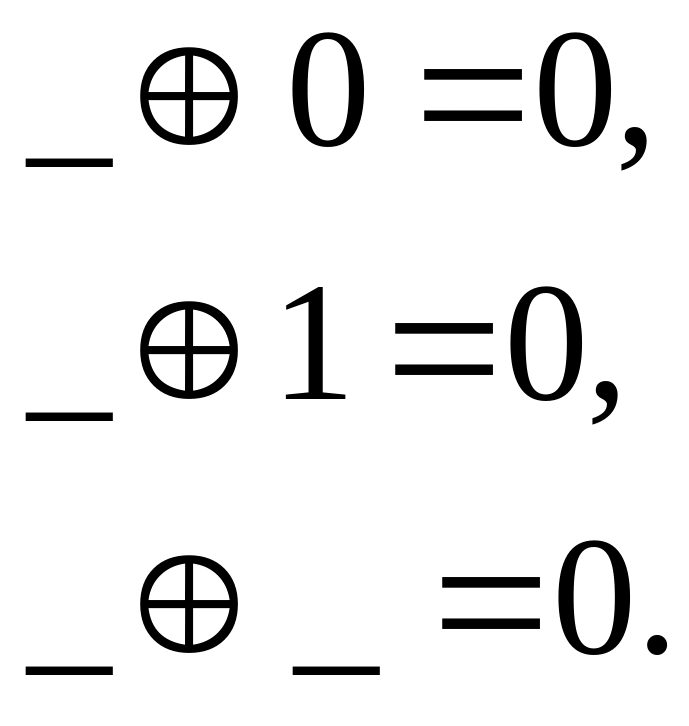3.3. Понятие интервала функции.

Представим БФ в виде гиперкуба, каждой вершине которого соответствует взаимнооднозначно входной двоичный набор. Все вершины упорядочены по ярусам. В i-й ярус входят вершины, с i-м количеством единиц в своих наборах. Вершины соединены ребром, если соответствующие двоичные наборы отличаются только одним разрядом (конъюнкции этих наборов могут быть склеены).

Вершины, образующие гиперкубы, кубы, грани, ребра или просто отдельные вершины, в которых , порождают единичные интервалы этой функции. Пример на рис. 7 для функции .

Вершины, образующие гиперкубы, кубы, грани, ребра или просто отдельные вершины, в которых , порождают нулевые интервалы этой функции.

3 ярус 1 111

110 011

2 ярус 1 0 101 0

100 001

1 ярус 1 1 010 0

0 ярус 1 000

Рис. 7. Функция в виде гиперкуба с единичными интервалами – гранью и ребром.

Единичный интервал I_a называется максимальным, если не найдется другого единичного интервала I_b, включающего в себя I_a.

Единичные интервалы:

, , , , , , , , , , .

Максимальные интервалы: и .

Конъюнкция, соответствующая максимальному единичному интервалу функции, является простой импликантой этой функции. Таким образом, выражение, составленное в виде дизъюнкции максимальных интервалов функции, будет его сокращенной ДНФ.

Переход от совершенной формы к сокращенной произошел путем попарного сравнения конституент соседних ярусов, что существенно сократило число сравнений (в отличие от количества сравнений по принципу «каждая с каждой», равному , где К – количество конституент).

3.4. Слабоопределенные бф.

Слабоопределенные или неполностью определенные БФ характеризуются следующими признаками:

1. число переменных n велико;

2. количество конституент 1 и 0 намного меньше

Так как для части входных наборов значения функции могут быть любыми, то при выполнении минимизации слабоопределенных функций сначала требуется их доопределение, причем такое, которое не противоречит цели минимизации – получению наиболее краткого (простого) выражения функции. То есть при минимизации слабоопределенных функций добавляется дополнительный этап – доопределение неопределенных состояний или мажорирования исходной функции.

Этапы минимизации бф. Табл. 6

Полностью определенные БФ	Слабоопределенные БФ
Получение сокращенной формы. Получение тупиковых форм. Выбор среди тупиковых минимальной или кратчайшей форм.	Получение сокращенной формы исходной функции. Получение сокращенной формы мажорирующей функции. Получение тупиковых форм. Выбор среди тупиковых форм.

Покажем минимизацию слабоопределенной функции на примере, причем для наглядности выберем функцию от четырех переменных, чтобы проследить этапы минимизации по карте Карно-Вейча.

Дана

				x4							x4							x4
					x3							x3							x3
			1	-	-	-				1	1	1	1				1	1	1	1
x2			1	-	0	0	x2			1	1	0	0	x2			1	0	0	0
	x1		-	0	-	-		x1		0	0	0	0		x1		1	0	0	0
			-	-	1	1				1	1	1	1				1	1	1	1
			а)							б)							в)

Рис. 8. а) функция f с выделенными исходными единичными и нулевыми интервалами;

б) и в) варианты доопределения f в виде мажорирующих ее f’ и f”.

1. Получим сокращенную форму исходной функции любым, известным способом.

2. Получим сокращенную форму, состоящую из максимальных единичных интервалов за счет доопределения в 1 некоторых неопределенных состояний (доопределение в 1 всех неопределенных состояний может быть далеко не самым удачным вариантом как, например, в нашем случае), для чего используем таблицу различий.

В таблице различий строками являются единичные интервалы, а столбцами – нулевые интервалы исходной функции . Клетки таблицы заполняют последовательностями 1 и 0, полученными в результате поразрядного сложения по модулю 2 соответствующих разрядов строки и столбца:

Таблица различий. Табл. 7

Единичные интервалы		Нулевые интервалы
		011_	1101
a b c d	0 _ 0 0	0 0 1 0	1 0 0 1
a b c d	1 0 1 _	1 1 0 0	0 1 1 0

Разряды единичных интервалов идентифицированы буквами a,b,c,d. Таблица различий позволяет определить, какие переменные исходной конъюнкции (исходного единичного интервала) войдут в мажорирующий (максимальный интервал): те, по которым есть различие в знаке разряда. Если оставить в мажорирующей конъюнкции соответствующий разряд, то в 1 определяются те неопределенные состояния, которые этому разряду соответствуют.

Единичный интервал 0_00 имеет различие с нулевым интервалом 011_ в разряде с. Для обеспечения непересечения доопределяемой области с нулевой обязательно будет присутствовать в мажорирующей конъюнкции. Единичный интервал 0_00 также имеет различие с нулевым интервалом 1101 в двух разрядах: a и d. Для обеспечения непересечения доопределяемой области с нулевой включим в мажорирующую конъюнкцию , либо . Иллюстрация на рис.

				x4								x4
					x3								x3
			1								1
x2			1		0	0	x2				1		0	0
	x1			0					x1			0
					1	1							1	1
а) доопределение в 1 области (или мажорирует ).								б) доопределение в 1 области (или мажорирует ).

Рис. 9. Мажорирование конъюнкции .

Итак, по единичному интервалу 0_00 получаем покрытие , то есть два варианта максимальных единичных интервалов: ,

По единичному интервалу 101_ получаем покрытие Так как покрытие короче, чем , то по интервалу 101_ выбираем только , то есть .

СДНФ мажорирующей функции: :

3. Определим все варианты тупиковых форм 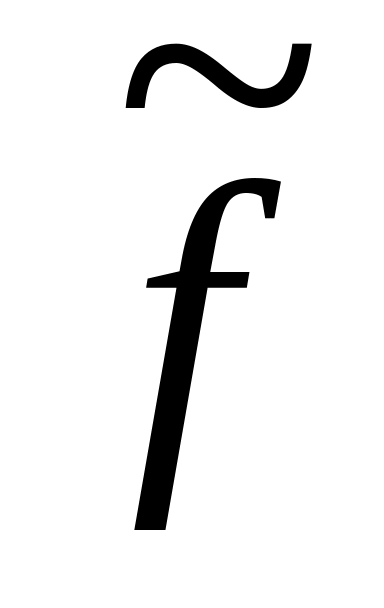по импликантной таблице, где в качестве простых импликант будут максимальные единичные интервалы , а вместо конституент единицы – единичные интервалы функции (таблица 8).

Табл. 8

Иденти-фикаторы	Максимальные единичные интервалы	Единичные интервалы функции f.
		0 _ 0 0	1 0 1 _
a	(0 _ 0 _)	X
b	( _ _ 0 0)	X
c	(_ 0 _ _)		X

Имеем покрытие П импликантной таблицы:

.

Тупиковых форм две (ac и bc):

.

4) Полученные тупиковые формы , мажорирующие , идентичны, так как имеют равную сложность и цену по Квайну и, следовательно, обе являются одновременно минимальными и кратчайшими.

На основании принципа двойственности все изложенные выше методы минимизации в классе ДНФ можно распространить и на класс КНФ. В таблице различий для определения покрытия нулевого интервала поменяем местами строки и столбцы. В импликантной таблице вместо простых импликант (максимальных единичных интервалов) строками станут простые имплиценты (максимальные нулевые интервалы), а столбцами конституенты нуля (нулевые интервалы) функции.

Задача 2. Для игрушки пирамиды, состоящей из 3-х колец различного диаметра, определить все возможные сочетания раскраски колец, если нижнее кольцо может быть раскрашено в фиолетовый, синий или зеленый цвет, среднее кольцо – в желтый, белый или голубой, а верхнее – только в красный.

Р ешение. Если известно, что III пирамида обязательно состоит из трех колец, то объединим три II обязательные части конструкции I функцией конъюнкция:

.

При этом каждая из частей имеет свою многовариантность раскраски , , Обобщенная структура раскраски будет представлять собой форму КНФ:

, а переход к форме ДНФ после раскрытия скобок покажет все возможные сочетания раскрасок:

Всего 9 вариантов.