
- •660041, Г. Красноярск, пр. Свободный, 82а
- •6 60041, Г. Красноярск, пр. Свободный, 82а
- •Задание и выбор варианта для его выполнения
- •Расчет величин токов непосредственным применением законов кирхгофа, методами контурных токов, узловых потенциалов и методом эквивалентного генератора
- •2.1. Анализ (расчет) сложных электрических цепей применением уравнений Кирхгофа
- •2.2. Анализ (расчет) сложных электрических цепей методом контурных токов
- •2.6.3 Анализ (расчет) сложных электрических цепей методом узловых потенциалов
- •2.6.4 Анализ (расчет) сложных электрических цепей методом эквивалентного генератора
- •2.5. Баланс мощностей в электрической цепи постоянного тока
- •2.6 Потенциальная диаграмма электрической цепи постоянного тока
- •Библиографический список
2.6.4 Анализ (расчет) сложных электрических цепей методом эквивалентного генератора
Метод эквивалентного генератора относится к классу методов, основанных на принципе упрощения электрической схемы цепи – когда с помощью тех или иных методов преобразования сложная схема электрической цепи упрощается до простой электрической схемы, в которой можно найти искомый ток по закону Ома. Сущность метода эквивалентного генератора состоит в следующем: любая, сколь угодно сложная схема линейной электрической цепи, может быть представлена относительно двух своих узлов в виде простой цепи – последовательного соединения источника ЭДС с внутренним сопротивлением (активного двухполюсника) и сопротивления нагрузки; ток в такой цепи легко найти по закону Ома.
На
рис. 2.8 представлена эквивалентная
электрическая схема так называемого
эквивалентного
генератора.
Она содержит эквивалентный генератор,
состоящий из ЭДС эквивалентного
генератора
![]() с внутренним сопротивлением
с внутренним сопротивлением
![]() (левая часть схемы рис. 2.8, выделенная
штриховой линией) и нагрузку этого
генератора
(левая часть схемы рис. 2.8, выделенная
штриховой линией) и нагрузку этого
генератора
![]() .
.
Если
к такой эквивалентной схеме привести
анализируемую цепь рис. 2.7, то затем
найти ток
![]() в этой цепи можно будет по закону Ома:
в этой цепи можно будет по закону Ома:
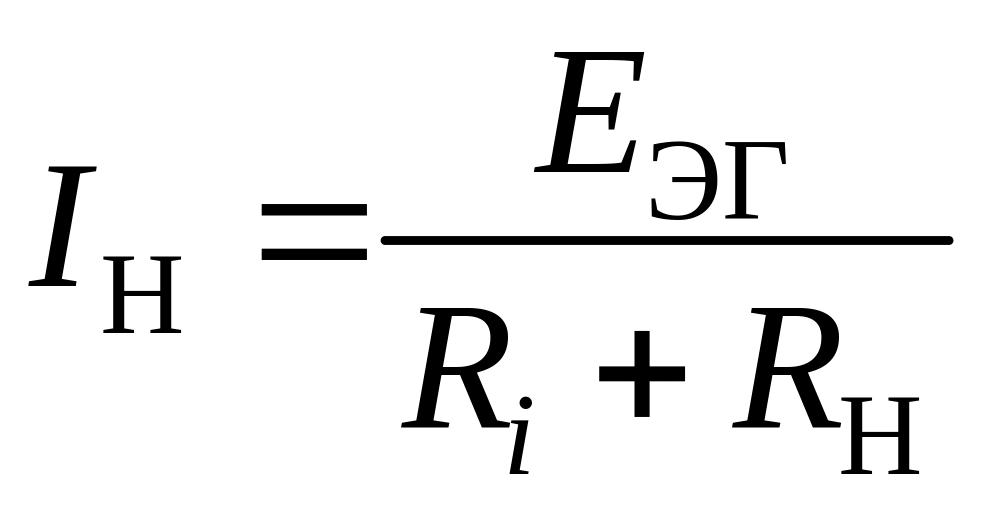 . (2.54)
. (2.54)
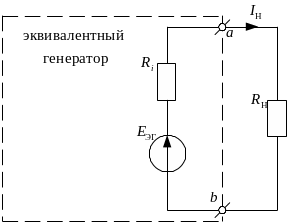
Рис. 2.8. Электрическая схема эквивалентного генератора.
Для рассмотрения метода эквивалентного генератора используем первоначальную анализируемую схему рис. 2.1 в виде, показанном ранее на рис. 2.5, где источники тока и первоначальной схемы рис. 2.1 преобразованы в эквивалентные им источники ЭДС и на схеме рис. 2.5. Исключив в схеме рис. 2.5 обозначения направлений обхода контуров цепи, получим схему, показанную на рис. 2.9.
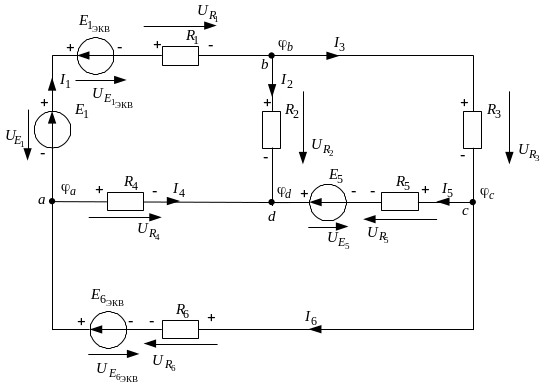
Рис. 2.9. Эквивалентная схема анализируемой электрической цепи
В
качестве искомого тока примем ток
![]() .
После этого схему рис. 2.9 перерисуем и
представим в виде, показанном на рис.
2.10.
.
После этого схему рис. 2.9 перерисуем и
представим в виде, показанном на рис.
2.10.
На
этом рисунке дополнительно введена
точка
![]() ,
а анализируемая схема представлена
так, чтобы было удобно рассматривать
её относительно точек
,
а анализируемая схема представлена
так, чтобы было удобно рассматривать
её относительно точек
![]() .
Тогда эквивалентный генератор (левая
относительно этих точек часть схемы) и
его нагрузка (правая относительно этих
точек часть схемы) будут соответствовать
расположению этих элементов, принятых
на рис. 2.8.
.
Тогда эквивалентный генератор (левая
относительно этих точек часть схемы) и
его нагрузка (правая относительно этих
точек часть схемы) будут соответствовать
расположению этих элементов, принятых
на рис. 2.8.
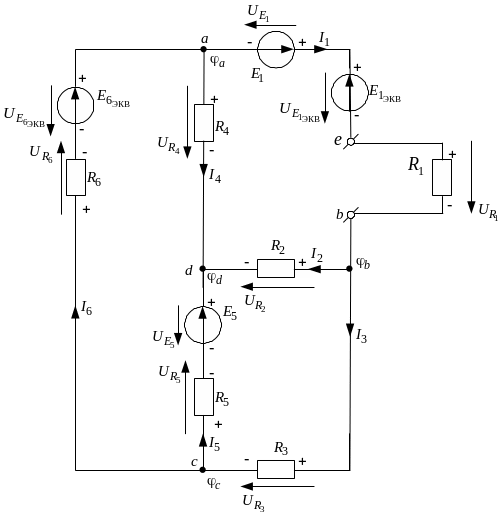
Рис. 2.10. Схема
анализируемой цепи с сопротивлением
,
выделенным в качестве нагрузки
эквивалентного генератора (искомый ток
![]() )
)
Для того, чтобы воспользоваться выражением (2.54) закона Ома для цепи, содержащей эквивалентный генератор и его нагрузку, необходимо привести левую относительно точек часть схемы сложной анализируемой цепи рис. 2.10 к виду, показанному на рис. 2.8 для эквивалентного генератора. Роль нагрузки схемы рис. 2.8 будет выполнять сопротивление схемы рис. 2.10.
Для преобразования схемы рис. 2.10 в схему рис. 2.8, следует определить ЭДС эквивалентного генератора и его внутреннее сопротивление .
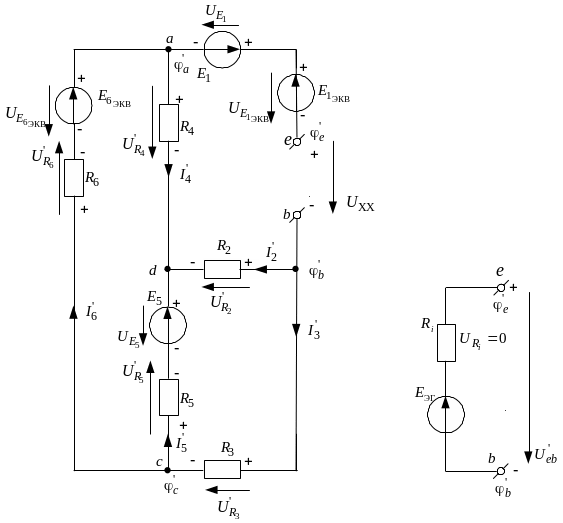
Для определения ЭДС эквивалентного генератора , удалим сопротивление в схеме рис. 2.10, получившуюся схему покажем на рис. 2.11, а, а затем заменим её эквивалентной схемой рис. 2.11, б.
 а б
а б
Рис. 2.11. Схема анализируемой цепи в режиме холостого хода (а));
эквивалентная схема анализируемой цепи в виде схемы
эквивалентного генератора (б))
После таких преобразований, когда анализируемая цепь рис. 2.10 переведена в режим холостого хода относительно точек (рис. 2.11, а), естественно, режим её работы изменится: изменятся токи ветвей и падения напряжений на сопротивлениях. Это изменение режима работы цепи отражено на рис. 2.11, а тем, что все обозначения токов ветвей и падений напряжений на сопротивлениях имеют верхний индекс «штрих».
Установление
режима холостого хода относительно
точек
приводит к тому, что ток во внешней цепи
генератора, эквивалентного анализируемой
цепи (рис. 2.11, б),
равен нулю, падения напряжения
![]() на внутреннем сопротивлении генератора
и все напряжение эквивалентного
генератора
оказывается приложенным к точкам
и
этой цепи. Таким образом, ЭДС
эквивалентного генератора равно
напряжению холостого хода анализируемой
схемы относительно разомкнутых клемм
схемы. То
есть, условие обеспечения холостого
хода в первой ветви рис. 2.10, ток
которой следует определить, выглядит
так:
на внутреннем сопротивлении генератора
и все напряжение эквивалентного
генератора
оказывается приложенным к точкам
и
этой цепи. Таким образом, ЭДС
эквивалентного генератора равно
напряжению холостого хода анализируемой
схемы относительно разомкнутых клемм
схемы. То
есть, условие обеспечения холостого
хода в первой ветви рис. 2.10, ток
которой следует определить, выглядит
так:
![]() , (2.55)
, (2.55)
![]() . (2.56)
. (2.56)
Тогда
можно найти ЭДС эквивалентного генератора
,
показанного на рис. 2.11, б,
которое оказывается равным напряжению
холостого хода
![]() (рис. 2.11, а):
(рис. 2.11, а):
![]() , (2.57)
, (2.57)
оно
же оказывается равным напряжению
![]() (рис. 2.11 б):
(рис. 2.11 б):
![]() , (2.58)
, (2.58)
а падение напряжения на внутреннем сопротивлении эквивалентного генератора рис. 2.11, б при этом равно нулю:
![]() . (2.59)
. (2.59)
Выражение
(2.58) показывает, каким образом можно
определить напряжение холостого хода
и эквивалентного генератора
– они равны разности потенциалов
![]() между точками
и
схемы анализируемой цепи при холостом
ходе в ветви определяемого тока. При
этом остается определить указанные
потенциалы любым известным методом
расчета сложных электрических цепей.
между точками
и
схемы анализируемой цепи при холостом
ходе в ветви определяемого тока. При
этом остается определить указанные
потенциалы любым известным методом
расчета сложных электрических цепей.
Второй неизвестной величиной в выражении (2.54) является внутреннее сопротивление эквивалентного генератора. Для его определения необходимо найти входное сопротивление схемы рис. 2.11, а, которое и будет этим сопротивлением . При этом наличие источников ЭДС и источников тока не имеет значения для сопротивления схемы, так как их внутренние сопротивления равны, соответственно, либо нулю, либо бесконечности. Учитывая, что внутреннее сопротивление источников ЭДС нулевое и на величины сопротивлений ветвей не влияет, преобразуем схему рис. 2.11, а, содержащую источники ЭДС, в схему рис. 2.12, содержащую только сопротивления без источников.
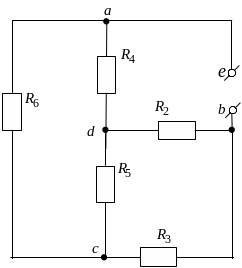
Рис. 2.12. Схема анализируемой цепи без источников ЭДС для определения внутреннего сопротивления эквивалентного генератора
Анализ схемы рис. 2.12 показывает, что в представленном виде эта схема не содержит последовательных и параллельных соединений. Соединения сопротивлений в этой схеме представляют собой звезды и треугольники:
-
сопротивления
,
![]() ,
,
![]() ,
соединенные между собой в узле
,
соединены звездой;
,
соединенные между собой в узле
,
соединены звездой;
-
сопротивления
,
![]() ,
,
соединенные между собой в узле
,
также соединены звездой;
,
,
соединенные между собой в узле
,
также соединены звездой;
- сопротивления , , , соединены между собой треугольником;
- сопротивления , , , соединены между собой также треугольником.
Для преобразования сложной электрической цепи, схема которой содержит соединения сопротивлений треугольниками и звездами, проще всего преобразовать один из треугольников сопротивлений в эквивалентную ему звезду.
Для схемы рис. 2.12 преобразуем, например, треугольник сопротивлений , , в эквивалентную ему звезду. Это преобразование иллюстрируется рис. 2.13, a ,b.
В
соответствии с правилом преобразования
треугольника сопротивлений
,
,
2.13, a,
в эквивалентную ему звезду
![]() ,
,
![]() ,
,
![]() 2.13, б,
запишем сопротивления лучей звезды
,
,
2.13, б
через сопротивления сторон треугольника
,
,
2.13, a:
2.13, б,
запишем сопротивления лучей звезды
,
,
2.13, б
через сопротивления сторон треугольника
,
,
2.13, a:
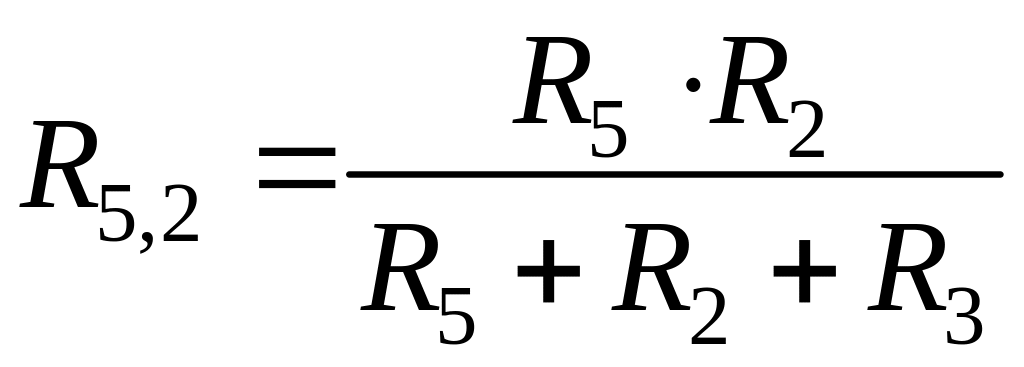 , (2.60)
, (2.60)
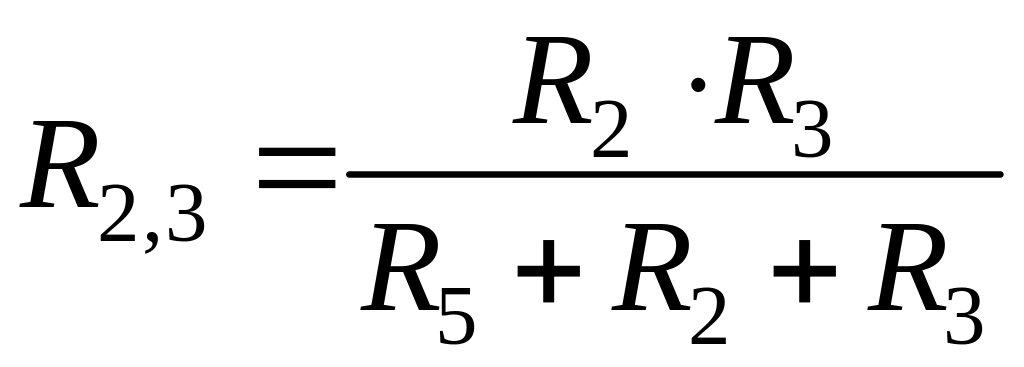 , (2.61)
, (2.61)
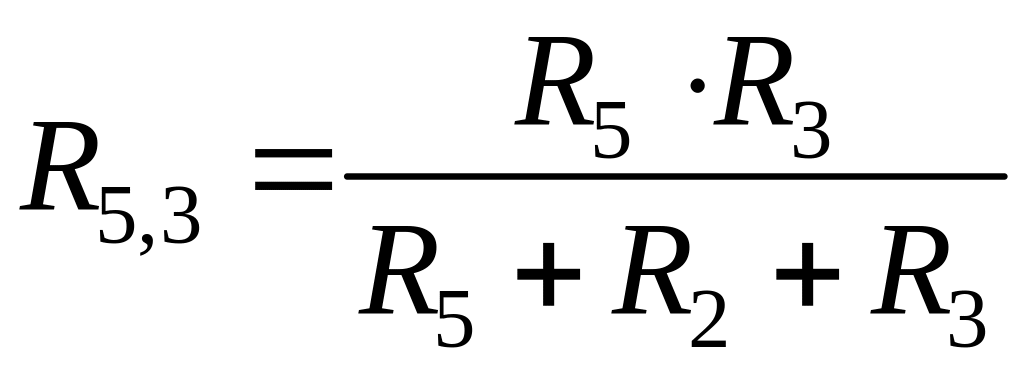 . (2.62)
. (2.62)
Образовавшийся
при этом дополнительный узел
![]() является промежуточным и во всех
последующих преобразованиях не участвует.
является промежуточным и во всех
последующих преобразованиях не участвует.
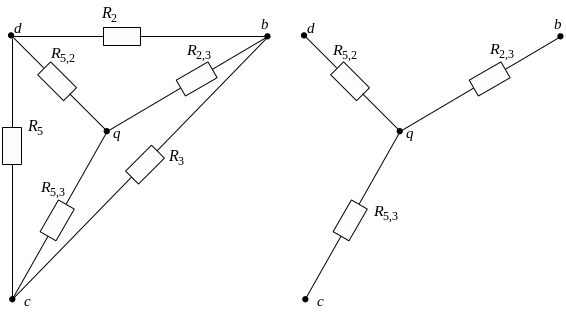
а б
Рис. 2.13. Преобразование
треугольника сопротивлений
![]() (а) в
(а) в
эквивалентную
звезду
![]() (б)
(б)
После
определения сопротивлений
,
,
лучей звезды рис. 2.13, б,
эквивалентной исходному треугольнику
рис. 2.13, а
сопротивлений
,
,
,
можно будет найти входное сопротивление
схемы рис. 2.12 относительно точек
![]() .
Это сопротивление и будет внутреннее
сопротивление эквивалентного генератора
схем рис. 2.8, рис. 2.11, б.
Для этого схему рис. 2.12 необходимо
перерисовать с учетом замены треугольника
сопротивлений
,
,
рис. 2.13, а
на эквивалентную ему звезду сопротивлений
,
,
,
рис. 2.13, б.
Такая схема показана на рис. 2.14. После
преобразования треугольника сопротивлений
,
,
на эквивалентную ему звезду сопротивлений
,
,
,
сопротивления
и
оказываются включенными последовательно,
и их общее сопротивление
.
Это сопротивление и будет внутреннее
сопротивление эквивалентного генератора
схем рис. 2.8, рис. 2.11, б.
Для этого схему рис. 2.12 необходимо
перерисовать с учетом замены треугольника
сопротивлений
,
,
рис. 2.13, а
на эквивалентную ему звезду сопротивлений
,
,
,
рис. 2.13, б.
Такая схема показана на рис. 2.14. После
преобразования треугольника сопротивлений
,
,
на эквивалентную ему звезду сопротивлений
,
,
,
сопротивления
и
оказываются включенными последовательно,
и их общее сопротивление
![]() равно:
равно:
![]() . (2.63)
. (2.63)
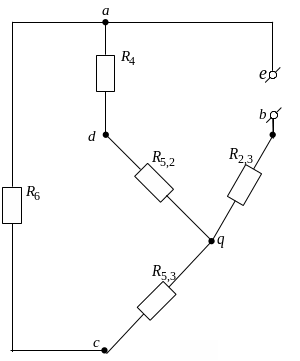
Рис. 2.14. Эквивалентная
схема анализируемой цепи для определения
внутреннего сопротивления эквивалентного
генератора
![]()
Сопротивления
и
также оказываются включенными
последовательно между собой и их общее
сопротивление
![]() равно их сумме:
равно их сумме:
![]() . (2.64)
. (2.64)
Полученные
в выражениях (2.63) и (2.64) сопротивления
и
оказываются включенными между собой
параллельно. Их общее сопротивление
![]() (относительно узлов
(относительно узлов
![]() и a)
равно:
и a)
равно:
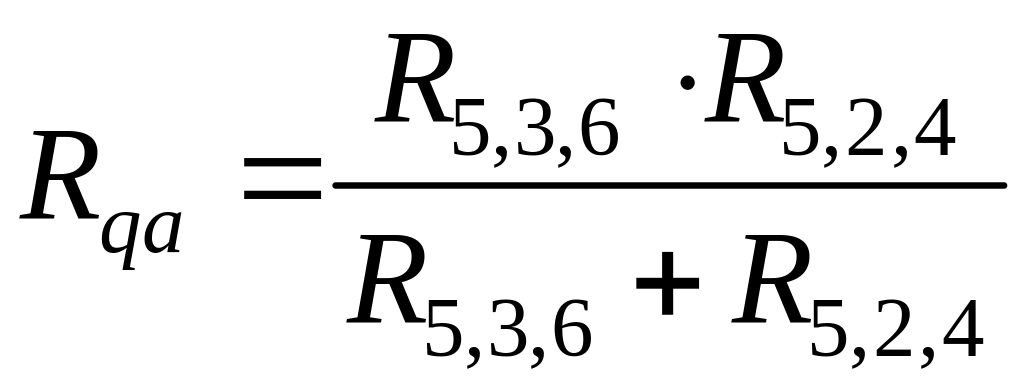 . (2.65)
. (2.65)
Сопротивление
оказывается включенным последовательно
с сопротивлением
(схема рис. 2.14). Их общее сопротивление
![]() относительно точек
схемы рис. 2.14, рис. 2.12, рис. 2.11, а,
оказывается равным внутреннему
сопротивлению
эквивалентного генератора рис. 2.11, б
и рис. 2.8:
относительно точек
схемы рис. 2.14, рис. 2.12, рис. 2.11, а,
оказывается равным внутреннему
сопротивлению
эквивалентного генератора рис. 2.11, б
и рис. 2.8:
![]() . (2.66)
. (2.66)
После определения величины ЭДС эквивалентного генератора (2.58) и его внутреннего сопротивления (2.66), можно найти величину искомого тока из выражения (2.54):
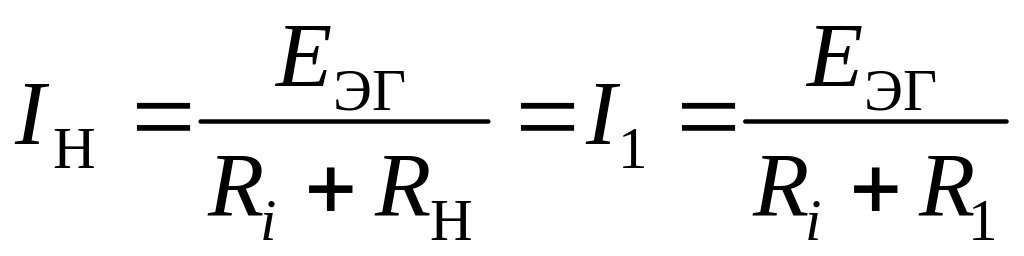 . (2.67)
. (2.67)
В
описанном нами методе эквивалентного
генератора внутреннее сопротивление
эквивалентного генератора было получено
путем преобразования исходной
анализируемой схемы рис. 2.9 к виду рис.
2.11, б
путем упрощения исходной схемы (2.60) –
(2.66). Однако, существует другой способ
расчета внутреннего сопротивления
эквивалентного генератора – через
использование параметров режимов
холостого хода (ХХ) и короткого замыкания
(КЗ) на выходе цепи (относительно точек
схемы, для которых определяется её
сопротивление). Мы не будем подробно
рассматривать этот способ определения
величины
,
запишем только выражение для определения
этого сопротивления через ток короткого
замыкания
![]() и напряжение холостого хода
:
и напряжение холостого хода
:
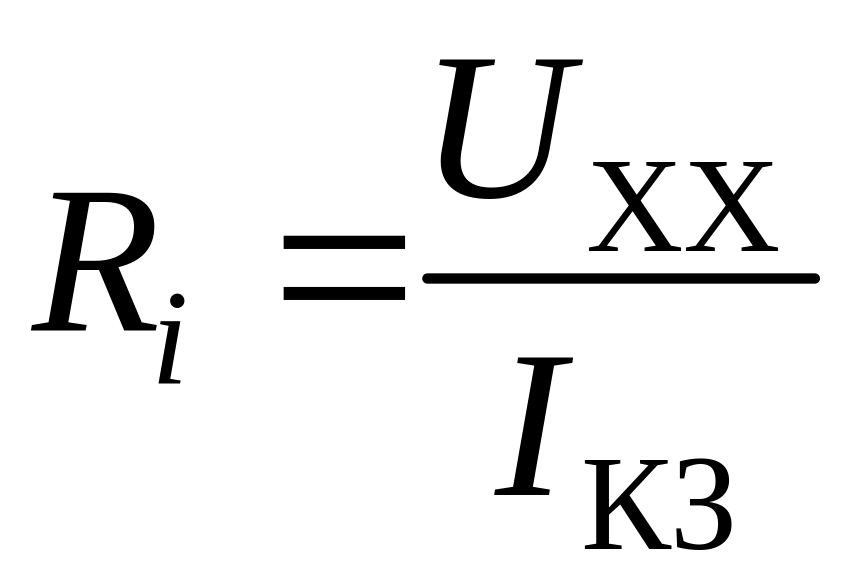 , (2.68)
, (2.68)
где режимы холостого хода и короткого замыкания определяются относительно точек схемы рис. 2.14.
Таким образом, найти входное сопротивление некоторой схемы относительно двух заданных точек схемы можно двумя основными путями: преобразованием сложной схемы в простую, или взяв отношение напряжения холостого хода к току короткого замыкания относительно заданных точек схемы.
Порядок расчета сложной электрической цепи методом эквивалентного генератора таков:
-
сопротивление
![]() ,
включенное между двумя точками сложной
электрической цепи, в котором необходимо
найти ток
,
включенное между двумя точками сложной
электрической цепи, в котором необходимо
найти ток
![]() ,
представляют нагрузкой и отключают от
остальной части цепи, создав таким
образом относительно этих точек цепи
режим холостого хода с напряжением
между ними;
,
представляют нагрузкой и отключают от
остальной части цепи, создав таким
образом относительно этих точек цепи
режим холостого хода с напряжением
между ними;
- остальную часть сложной цепи представляют активным двухполюсником с некоторой ЭДС и внутренним сопротивлением , последовательное включение которых представляет собой эквивалентный генератор;
-
любым известным способом рассчитывают
величину ЭДС эквивалентного генератора
![]() как напряжение холостого хода
относительно точек схемы, от которых
отключено сопротивление с искомым
током;
как напряжение холостого хода
относительно точек схемы, от которых
отключено сопротивление с искомым
током;
-
величину внутреннего сопротивления
генератора
![]() определяют либо как входное сопротивление
схемы относительно точек цепи, от которых
отключено сопротивление с искомым
током, либо как отношение напряжения
холостого хода
к току короткого замыкания
на этом же участке цепи;
определяют либо как входное сопротивление
схемы относительно точек цепи, от которых
отключено сопротивление с искомым
током, либо как отношение напряжения
холостого хода
к току короткого замыкания
на этом же участке цепи;
- искомый ток находят как частное от ЭДС эквивалентного генератора на величину суммы внутреннего сопротивления эквивалентного генератора и сопротивления ветви с искомым током.
