2.2. Анализ (расчет) сложных электрических цепей методом контурных токов

В соответствии с методом контурных токов (МКТ) предполагается, что в каждом из контуров течет свой контурный ток, не разветвляющийся в узлах электрической цепи. Такое предположение имеет целью уменьшить число одновременно решаемых уравнений до числа независимых контуров в схеме. После того, как эти специально введенные контурные токи буду найдены, можно из них рассчитать истинные токи ветвей. Такова сущность метода контурных токов.

Схема исходной анализируемой цепи рис. 2.1 в настоящем подразделе приведена к виду рис. 2.6, удобному для расчета токов методом контурных токов. Она отличается от предыдущей схемы рис. 2.5 тем, что вместо направлений обходов контуров, выбранных по часовой стрелке и обозначенных прерывистыми линиями, в схеме рис. 2.6 эти направления представляют собой направления протекания контурных токов . Обозначения полярностей и направлений падений напряжений на сопротивлениях в схеме рис. 2.6, в отличие от схемы рис. 2.5, отсутствуют, так как в методе контурных токов используются различные падения напряжений – и от токов ветвей (реально существующих в цепи) и от контурных токов (искусственно введенных токов). Кроме этого, в схеме рис. 2.6 исключены обозначения потенциалов узлов , соответственно. Обозначения падений напряжений , создаваемых соответственно источниками ЭДС , сохранены, так как они не зависят от тех или иных представлений токов в схеме.

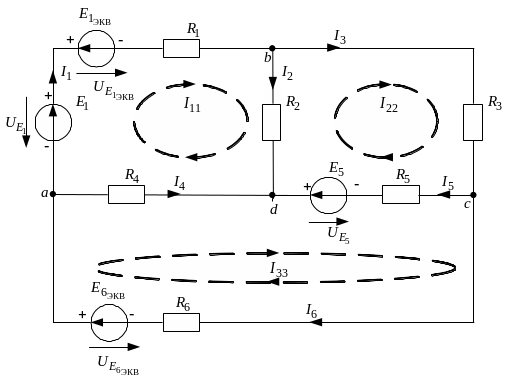
Рис. 2.6. Схема электрической цепи для расчета токов в цепи методом контурных токов

Между придуманными для упрощения расчетов контурными токами , , и реально существующими в цепи токами ветвей , , , , есть однозначное соответствие. В первом контуре, где течет абстрактный ток (из узла a через источник ЭДС , далее через источник ЭДС , затем через сопротивление , через узел b, через сопротивление и сопротивление и снова в узел a, никуда не ответвляясь), в первой ветви течет истинный (реально существующий в цепи) ток , и, поскольку в этой первой ветви больше никаких контурных токов нет, а направление контурного тока совпадает с направлением тока ветви , то очевидно, что ток первой ветви равен по величине и направлению контурному току :

. (2.18)

Аналогично этому, в третьей и шестой ветвях схемы:

, (2.19)

. (2.20)

Во второй ветви, где в направлении, совпадающем с направлением тока ветви , протекает контурный ток первого контура , а в направлении, противоположном току ветви , протекает контурный ток второго контура , ток второй ветви можно определить как:

. (2.21)

Аналогично в четвёртой и пятой ветвях:

, (2.22)

. (2.23)

Таким образом, выражения (2.18) – (2.23) определяют все токи ветвей схемы рис. 2.6 через контурные токи .

Для того, чтобы найти контурные токи , , , следует составить для них уравнения по второму закону Кирхгофа. Это делают аналогично тому, как ранее составлялись аналогичные уравнения для токов ветвей , , , , (2.13) – (2.15), но в предположении, что в контурах текут только контурные токи , , .

В первом контуре (где протекает контурный ток ), падения напряжения на сопротивлениях первого контура , и будут таковы: от протекающего в них по часовой стрелке контурного тока падения напряжений берутся положительными; от протекающего в сопротивлении контурного тока , который противоположен контурному току в этом сопротивлении, падение напряжения берется со знаком «минус»; от протекающего в сопротивлении контурного тока , который противоположен контурному току в этом сопротивлении, падение напряжения также берется со знаком «минус». Тогда сумма падений напряжений на элементах первого контура с учетом падений напряжения на источниках ЭДС, входящих в первый контур, по второму закону Кирхгофа:

. (2.24)

Аналогично составим уравнение второго закона Кирхгофа для второго и третьего контуров анализируемой схемы рис. 2.6:

, (2.25)

. (2.26)

Эти уравнения (2.24) – (2.26) носят название контурных уравнений, или уравнений метода контурных токов для анализируемой схемы. Контурные уравнения (2.24) – (2.26) для удобства восприятия можно записать в виде системы уравнений:

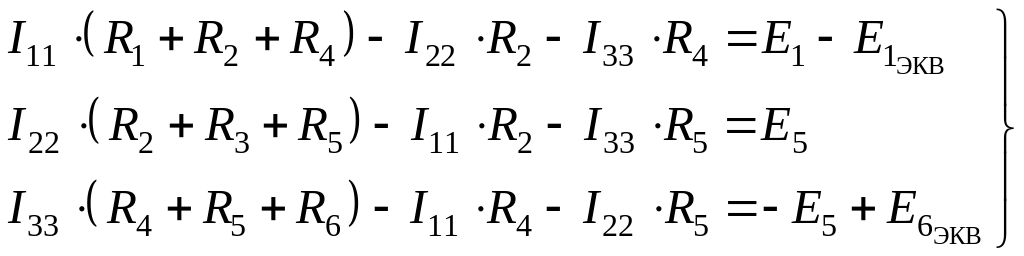. (2.27)

Закономерность, наблюдаемая в получившихся уравнениях метода контурных токов (2.27), дает правило составления контурных уравнений: количество уравнений метода контурных токов для заданной сложной схемы электрической цепи будет равно числу независимых контуров, имеющихся в этой цепи. В левой части уравнений метода контурных токов записывают алгебраическую сумму падений напряжений на сопротивлениях контура от всех контурных токов, протекающих в этих сопротивлениях, а в правой части уравнений метода контурных токов записывают алгебраическую сумму ЭДС, входящих в этот контур.

Введя понятия контурного сопротивления, а также общего сопротивления смежных контуров, можно упростить вид полученных выше уравнений метода контурных токов (2.27). Поясним это далее.

Контурное сопротивление есть сумма сопротивлений, входящих в состав рассматриваемого контура.

Например, для первого контура рассматриваемой схемы электрической цепи рис. 2.6, контурное сопротивление – это есть сумма сопротивлений первого контура , и :

. (2.28)

Аналогично для второго и третьего контуров схемы рис. 2.6:

, (2.29)

. (2.30)

где и – контурные сопротивления второго и третьего контуров.

Общее сопротивление смежных (соседних) контуров есть сопротивление, через которое текут два контурных тока – ток рассматриваемого контура и ток смежного с ним контура.

Общее сопротивление для первого и второго контуров обозначим как , или . Оно равно:

. (2.31)

Общее сопротивление для второго и третьего контуров обозначим как , или :

. (2.32)

Общее сопротивление для первого и третьего контуров обозначим как , или :

. (2.33)

Учитывая введенные понятия контурных сопротивлений (выражения (2.28) – (2.30)) и общего сопротивления смежных контуров (выражения (2.31) – (2.33)), систему контурных уравнений (2.27) можно записать:

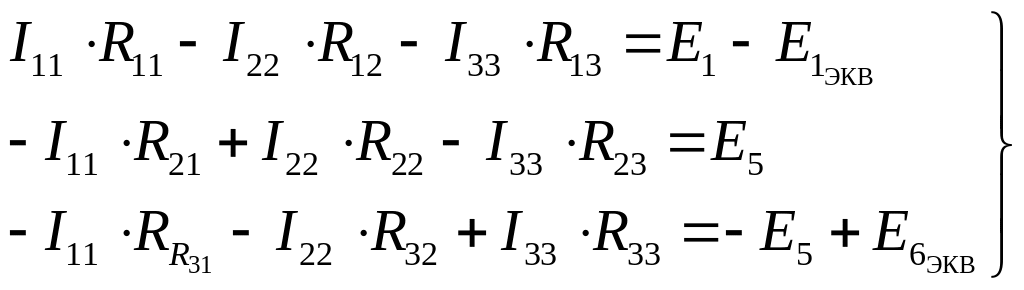. (2.34)

После того, как система уравнений метода контурных токов преобразована из вида (2.27) к виду (2.34), можно изложить формулировку правила составления контурных уравнений в таком виде:

- в левой части каждого контурного уравнения записывают произведение контурного тока рассматриваемого контура на контурное сопротивление этого контура со знаком «плюс», плюс произведение каждого из имеющихся общих сопротивлений рассматриваемого и смежных контуров на контурный ток соответствующего смежного контура, если он сонаправлен с контурным током рассматриваемого контура, или минус это произведение, если ток смежного контура направлен противоположно контурному току рассматриваемого контура;

- в правой части каждого контурного уравнения записывают источники ЭДС, входящие в состав рассматриваемого контура со знаком «плюс», если стрелки внутри источников сонаправлены с контурным током рассматриваемого контура, и со знаком «минус», если стрелки внутри источников направлены противоположно контурному току рассматриваемого контура.

В полученную систему уравнений (2.34) следует подставить численные значения сопротивлений, источников ЭДС и тока и решить эту систему любым известным способом.

После решения системы уравнений (2.34) полученные значения контурных токов подставляют в уравнения, выражающие токи ветвей через контурные токи (2.18) – (2.23). Полученные таким образом значения токов ветвей проверяют подстановкой их значений в уравнения второго закона Кирхгофа (2.16).

Таким образом, последовательность расчета (анализа) сложных электрических и радиоэлектронных схем методом контурных токов выглядит следующим образом:

- заданную для анализа (расчета) электрическую схему перерисовывают с указанием на ней направлений искомых токов ветвей и контурных токов;

- источники тока пересчитывают в эквивалентные источники ЭДС;

- записывают соотношения между токами ветвей и контурными токами в схеме;

- записывают систему уравнений по второму закону Кирхгофа для контурных токов, либо получают контурные уравнения подстановкой соотношений между токами ветвей и контурными токами в уравнения второго закон Кирхгофа для токов ветвей;

- решают систему уравнений второго закона Кирхгофа для контурных токов (систему контурных уравнений) и получают численные значения контурных токов в схеме;

- через соотношения токов ветвей и контурных токов рассчитывают значения токов во всех ветвях схемы;

- полученные значения токов ветвей подставляют в уравнения второго закона Кирхгофа для токов ветвей и проверяют правильность решения уравнений.

Поскольку число одновременно решаемых уравнений в методе контурных токов равно числу независимых контуров в схеме анализируемой цепи, то наиболее целесообразно использовать метод контурных токов для расчета цепей, в которых число контуров минимально, чтобы число уравнений метода контурных токов было также минимальным.