
- •Асимптоти функції.
- •Запитання для самоконтролю.
- •Завдання.
- •Дослідження функцій на монотонність.
- •Запитання для самоконтролю.
- •Завдання.
- •Дослідження функцій на опуклість.
- •Запитання для самоконтролю.
- •Завдання.
- •Вибрані задачі інтегрального числення.
- •Запитання для самоконтролю.
- •Завдання.
- •Графічний спосіб розв’язування рівнянь, нерівностей, систем.
- •Завдання.
- •Самостійні роботи.
- •Контрольні роботи
Графічний спосіб розв’язування рівнянь, нерівностей, систем.
Графічний спосіб розв’язування лінійних рівнянь; рівнянь, що містять знак модуля. Графічний спосіб розв’язування квадратичних рівнянь, нерівностей з параметром. Графічний спосіб розв’язування систем двох лінійних рівнянь з двома невідомими, систему рівнянь з параметром. Графічний спосіб розв’язування логарифмічних, тригонометричних рівнянь і нерівностей.
Завдання.
46. Розв’язати графічно рівняння.
1) |
5) |
9) |
2) |
6) |
10) |
3) |
7) |
11) |
4) |
8)
|
12)
|
47*. Розв’язати лінійні рівняння з параметром.
1)
|
3)
|
5)
|
2)
|
4) |
6)
|
48. Розв’язати графічно систему рівнянь.
1) |
2) |
3) |
4) |
49*. При яких значеннях параметра а система рівнянь має 2 розв’язки?
1) |
2) |
3) |
4)
|
50*. Визначити кількість рішень системи в залежності від параметра а.
1)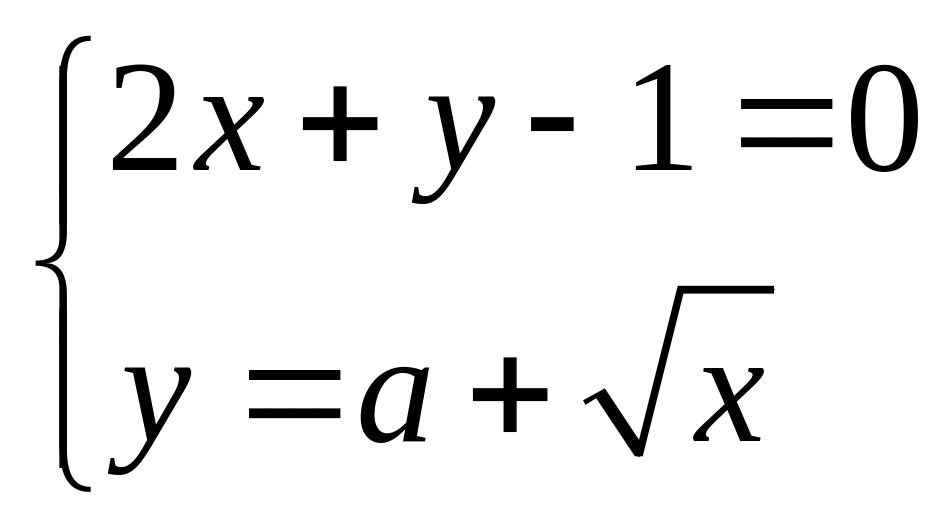 ;
2)
;
2)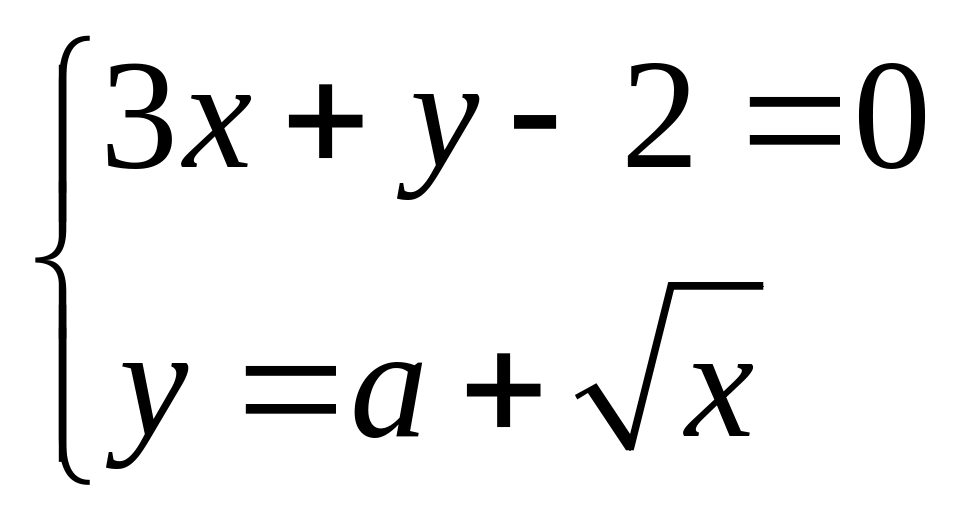 .
.
51*. При яких значеннях параметра а система рівнянь має єдиний розв’язок?
1)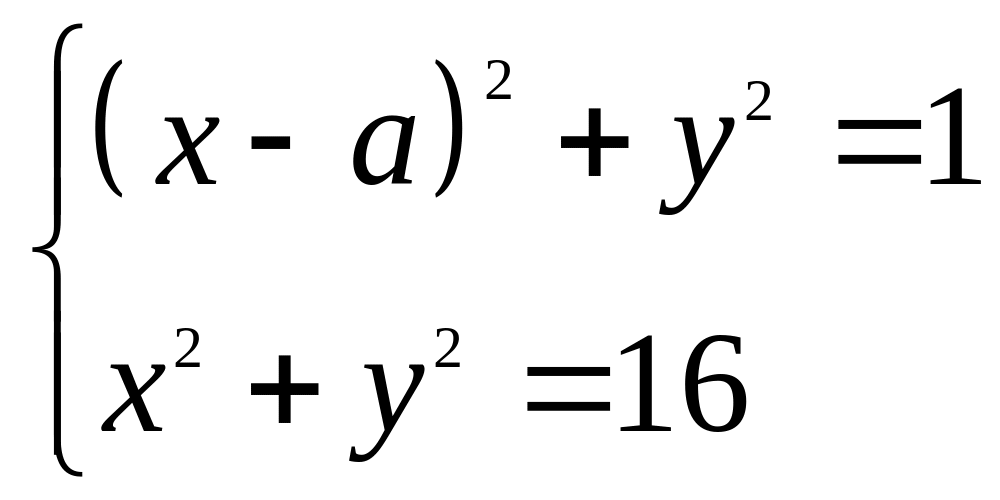 ;
2)
;
2) .
.
52. Розв’язати графічно систему нерівностей.
1) |
2) |
3) |
4) |
53. Розв’язати нерівність графічно і перевірити її аналітично.
1)
|
2) |
3) |
4)
|
5) |
6) |
7) |
8) |
9)
|
10) |
11)
|
12)
|
54*.
При
яких значеннях параметра m
нерівність
![]() виконується при в сих значеннях
виконується при в сих значеннях
![]() ?
?
55*. Розв’язати графічно нерівності з параметром.
1) |
2) |
3) |
4) |
56. Розв’язати графічно рівняння
1) |
5) |
9)
|
2) |
6) |
10)
|
3) |
7) |
11) |
4) |
8) |
12)
|
57. Визначити графічно кількість дійсних коренів рівняння.
1) |
2) |
3) |
4) |
58. Розв’язати графічно систему рівнянь.
1) ;
2)
;
2)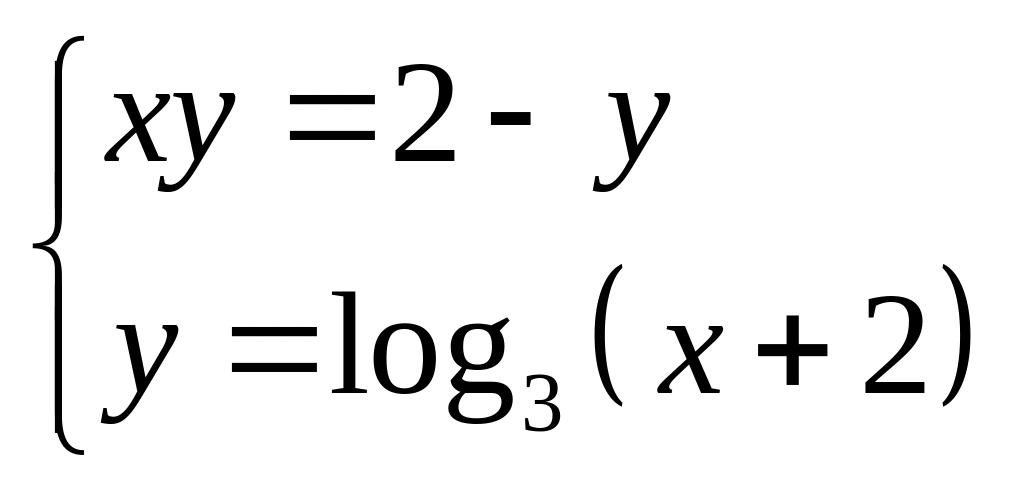 .
.
59. Розв’язати нерівність графічно.
1)![]() ;
2)
;
2)![]() ;
;
3)![]() ;
4)
;
4)![]() .
.
60. Розв’язати графічно систему нерівностей.
1)
 ;
2)
;
2)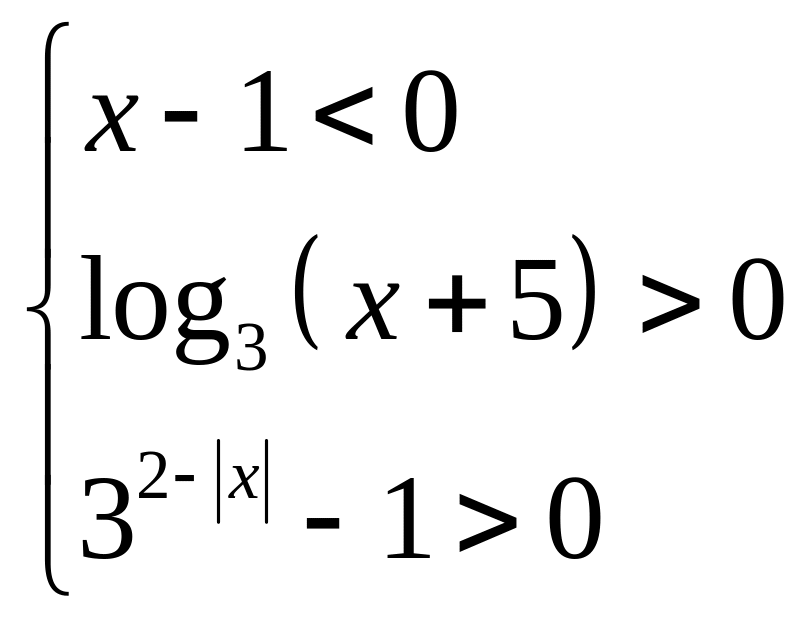 .
.
61*. Визначити кількість розв’язків рівняння в залежності від параметра а.
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() .
.
62. Розв’язати графічно рівняння.
1) |
5) |
9) |
2) |
6) |
10) |
3) |
7) |
11) |
4) |
8) |
12*) |
63. Розв’язати графічно систему рівнянь.
1) ;
2)
;
2)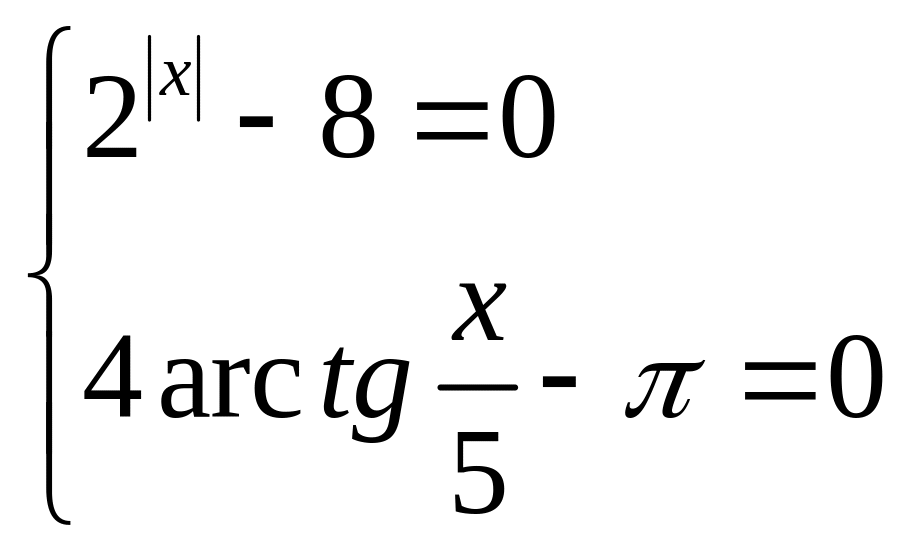 .
.
64*. При яких значеннях параметра а рівняння має розв’язки на інтервалі
![]() ?
?
1)![]() ;
2)
;
2)![]() ;
;
3)![]() ;
4)
;
4)![]() ;
;
5)![]() ;
6)
;
6)![]() ;
;
7)![]() ;
8)
;
8)![]() .
.
65*. При яких значеннях параметра а рівняння має єдиний корінь на вказаному інтервалі.
1)![]() ;
;
![]() ;
2)
;
2)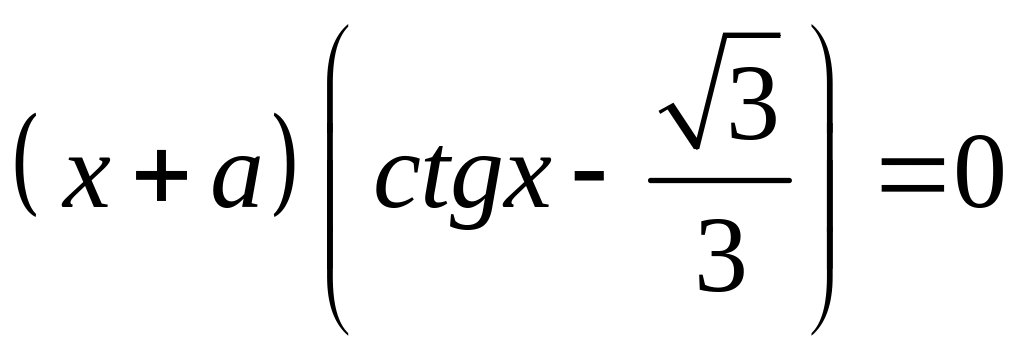 ;
;
![]() ;
;
3)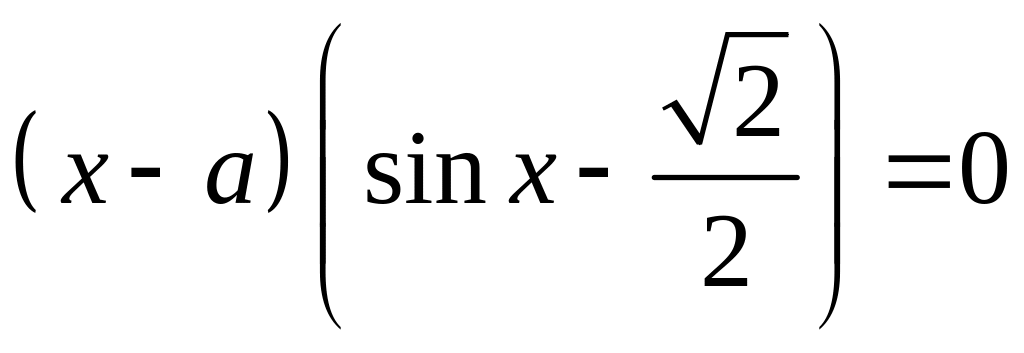 ;
;
![]() ;
4)
;
4)![]() ;
;
![]() ;
;
5)![]() ;
;
![]() ;
6)
;
6)![]() ;
.
;
.
66. Розв’язати графічно рівняння.
1)![]() ;
2)
;
;
2)
;
3)![]() ;
4)
;
4)![]() ;
;
5)![]() ;
6)
;
6)![]() ;
;
7)![]() ;
8)
;
8)![]() ;
;
9)![]() ;
10)
;
10)![]() .
.
67. Розв’язати графічно нерівність.
1)![]() ;
2)
;
2)![]() ;
;
3)![]() ;
4)
;
4)![]() ;
;
5)![]() ;
6)
;
6)![]() .
.
68*. Визначити кількість розв’язків рівняння в залежності від параметра а.
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)
![]() ;
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)
![]() ;
;
9)![]() ;
10)
;
10)![]() .
.
69*. При яких значеннях параметра а система рівнянь має 3 розв’язки?
1) ;
2)
;
2) ;
3)
;
3)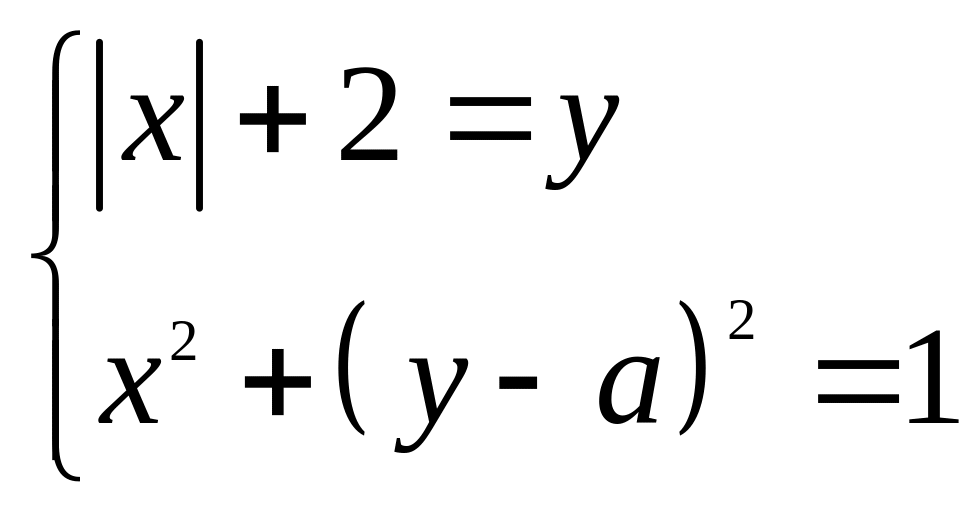 ;
;
4)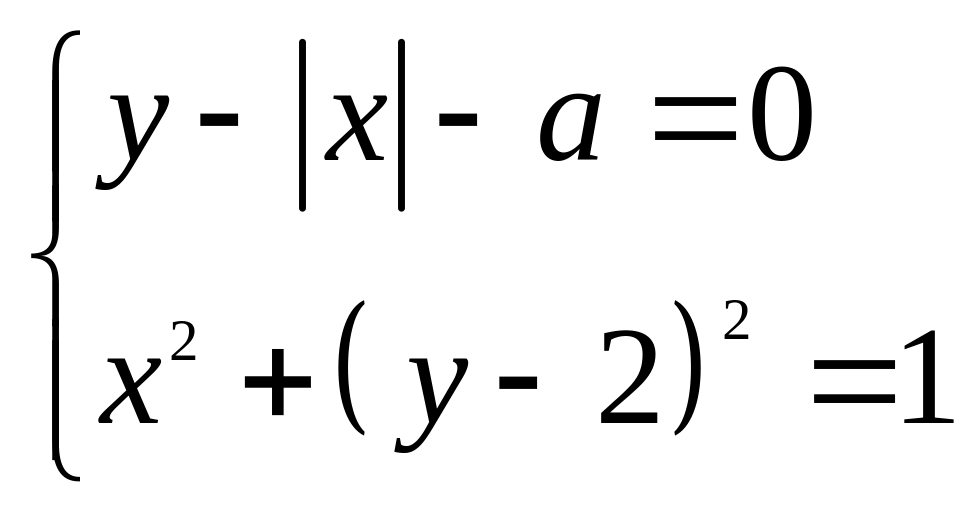 ;
5)
;
5)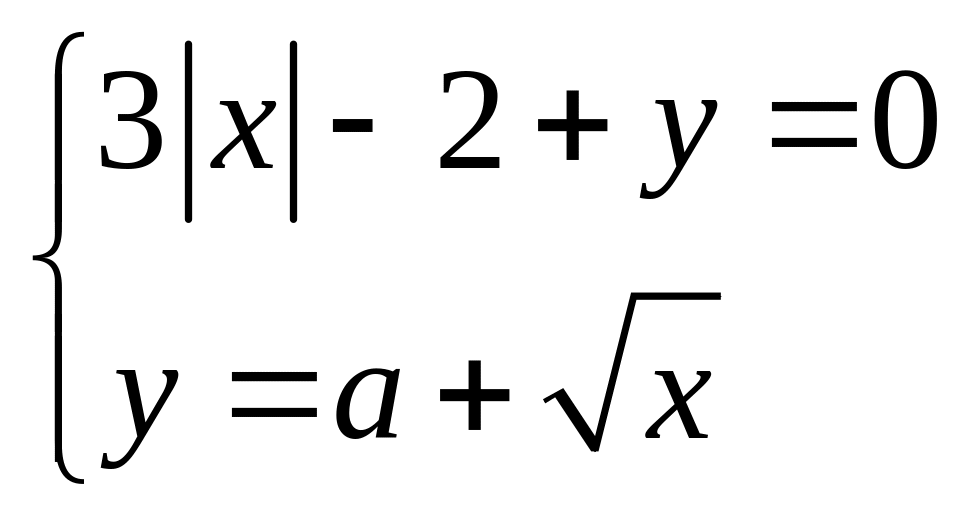 ;
6)
;
6)![]() .
.
70*. Визначити кількість розв’язків рівняння в залежності від параметра а.
1)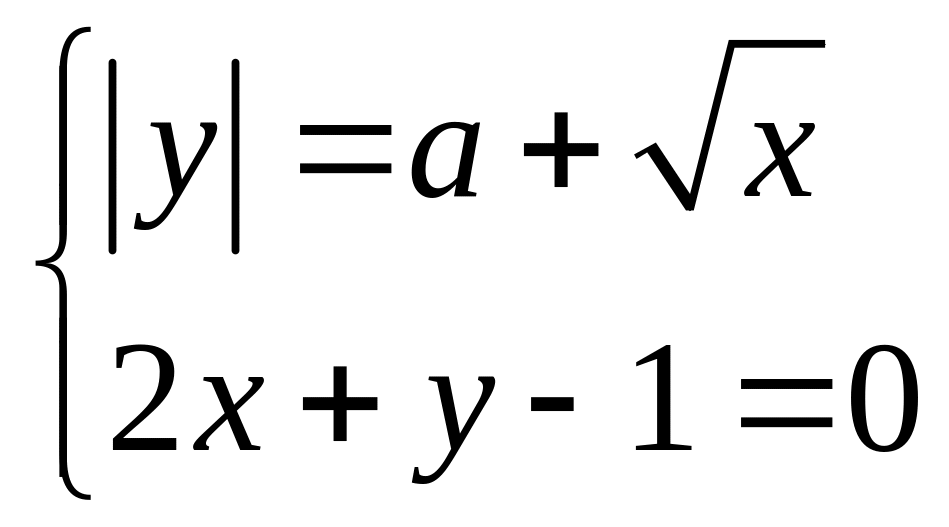 ;
2)
;
2)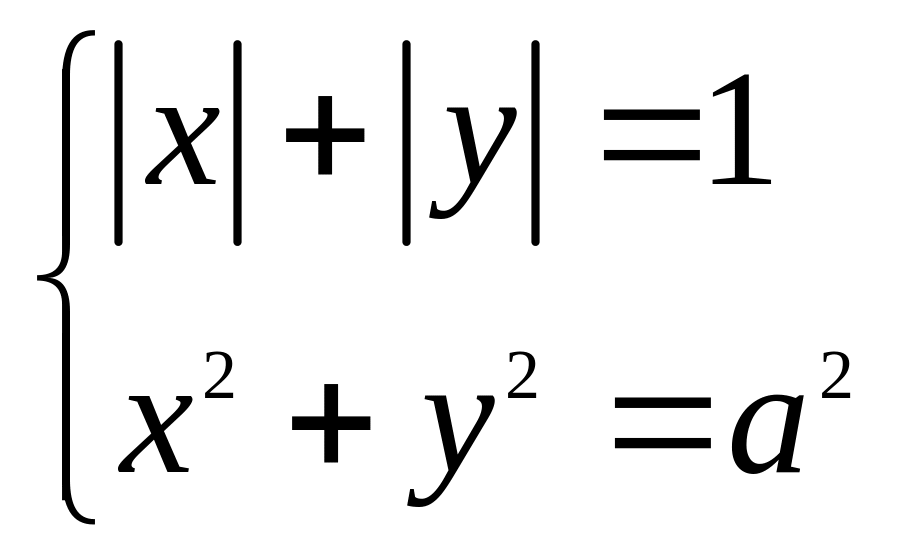 ;
3)
;
3)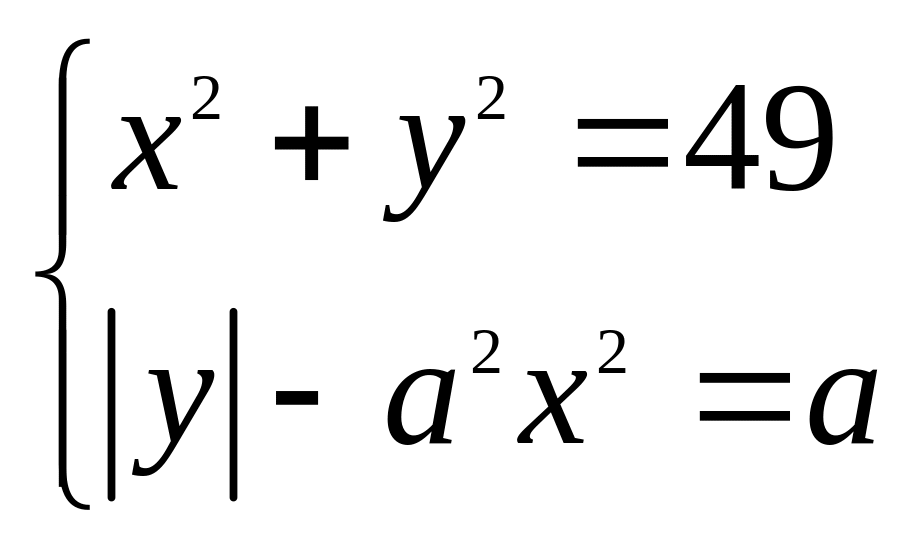 ;
;
4)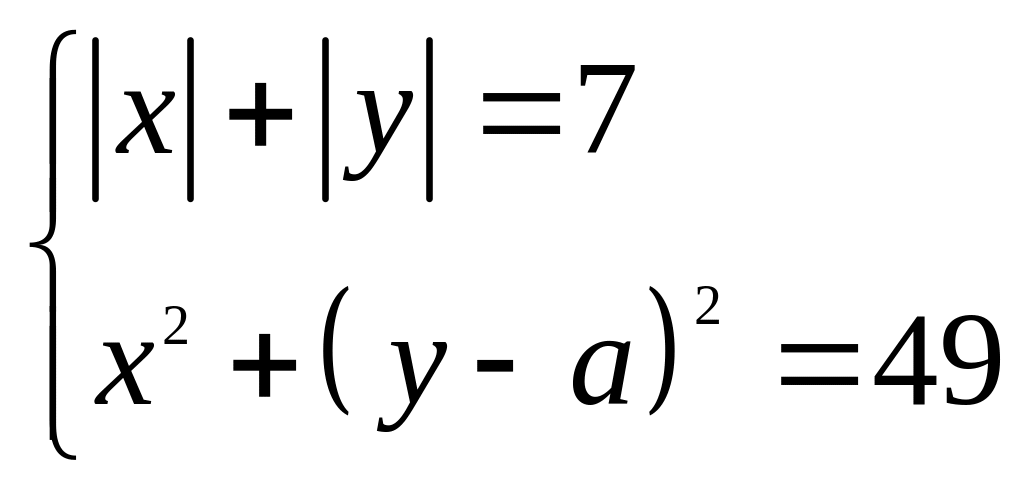 ;
5)
;
5)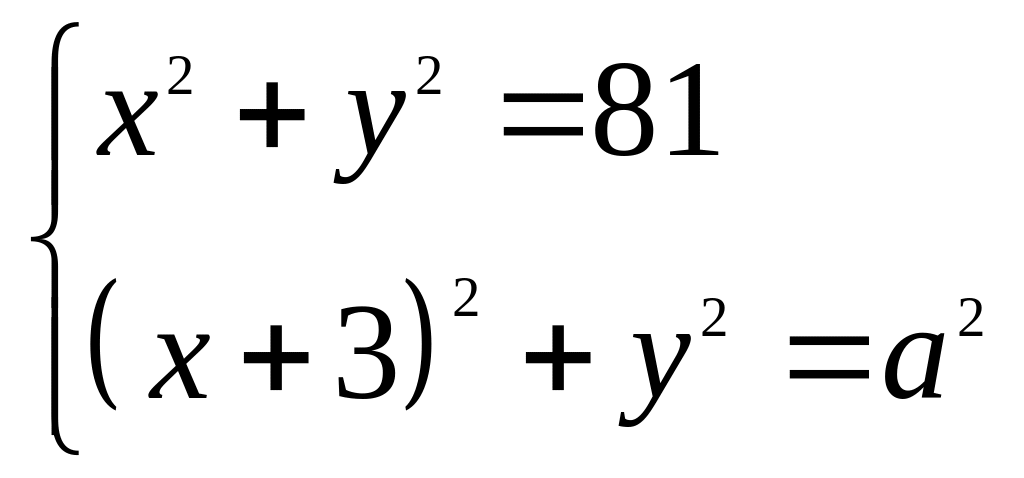 .
.
Побудова графіків функцій, зв’язаних з функцією
антьє і мантисою.
Поняття
цілої частини числа. Поняття дробової
частини числа. Властивості антьє та
мантиси. Побудова графіків функцій,
зв’язаних з функцією
![]() ,
,
![]() ,
де
,
де
![]() .
Рівняння
з цілою і дробовою частиною. Нерівності
.
Рівняння
з цілою і дробовою частиною. Нерівності
з цілою і дробовою частинами.
Запитання для самоконтролю.
Дайте визначення цілої частини числа.
Дайте визначення дробової частини числа.
Сформулюйте властивості функцій та де .
Завдання.
71. Записати дані числа у вигляді суми цілої і дробової частини.
а) 2,01; π; 5; -2,37; -6,07; -7; -π;
б) 4,03;
е;
g;
π; -1,48; -6,55; -7,05;![]() ;
;
в) 1,17;
-6,06; -3π;
![]() ;
0,199; -0,107.
;
0,199; -0,107.
72. Знайти:
а) цілу частину числа:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
-8,88; 10,01; 44,44;
;
-8,88; 10,01; 44,44;
![]() ;
;
б) дробову частину числа:
3,2;
1,0167; -0,575; -2,14; -7,17;
![]() ;
;
![]() ;
;
в) найбільше ціле число, яке задовольняє нерівність: 1,6-(3-2x) < 5;
г) найменше ціле число, яке задовольняє нерівностям:
1) 8(6-y)<24,2-7y;
2) (cos5)5x-1≤ 1.
73. Визначити кількість розв’язків рівняння, нерівності.
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
;
4)![]() ;
5)
;
5)![]() .
.
74*. При якому найбільшому значенні параметра а рівняння
![]() має
рівно 4корені?
має
рівно 4корені?
75. Знайти:
а) найбільший цілий від’ємний розв’язок нерівності:
1)
![]() ;
;
2)
![]() ;
;
б) скільки
натуральних чисел на проміжку
![]() є розв’язками
нерівності
є розв’язками
нерівності
![]() .
.
76. Знайти цілу частину значення виразу:
1)
![]() ;
2)
;
2)![]() ;
;
3)
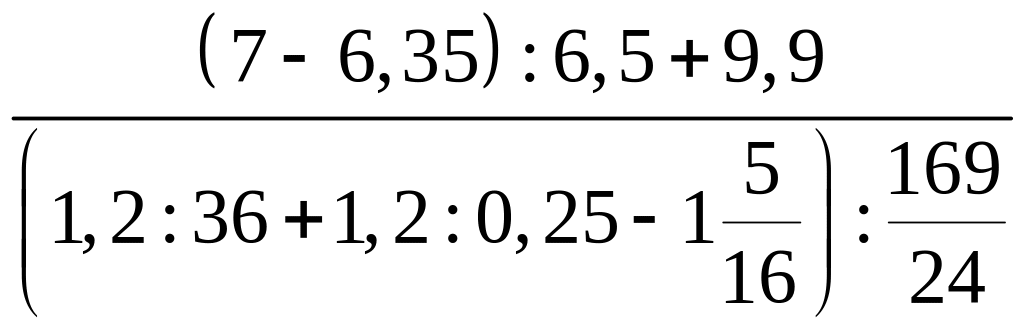 ;
4)
;
4) .
.
77.Побудувати графік функції.
1)
![]() ;
2)
;
;
2)
;
3)![]() ;
4)
;
4)![]() .
.
78.Побудувати графік функції: . Знайти:
1)
![]()
2) значення аргументу, при яких значення функції дорівнює -4; 7; 0; 1;
3)
![]() ;
;
4*)
значення параметра а,
при якому нерівність
![]() має рішення;
має рішення;
5*) значення параметра а , при яких система рівнянь
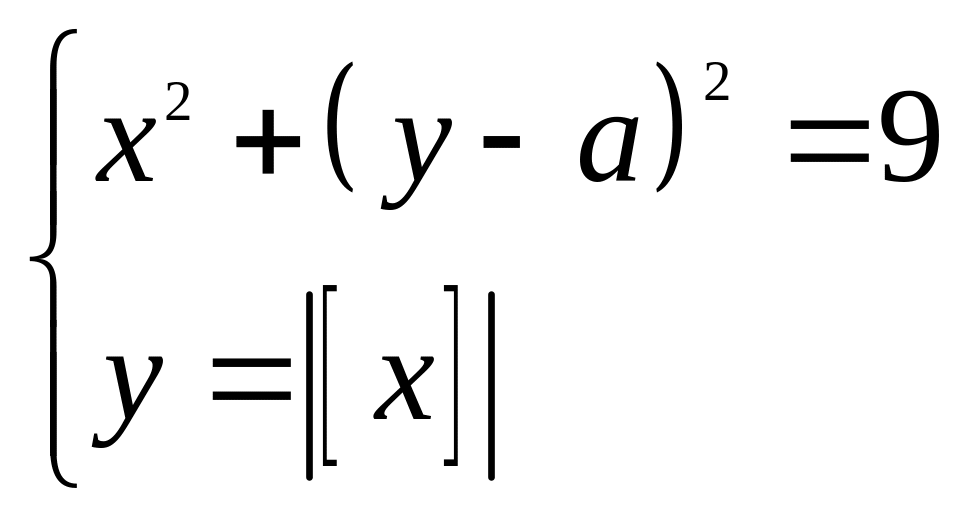 має
3 розв’язки.
має
3 розв’язки.
79. Розв’язати графічно рівняння.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
;
4)![]() ;
5)
;
5)![]() .
.
80. Розв’язати систему рівнянь, нерівностей.
1)
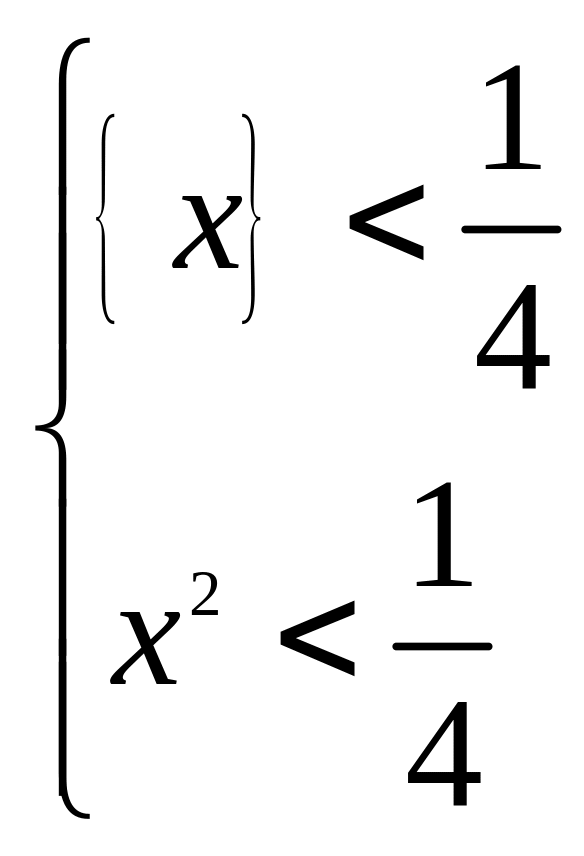 ;
2)
;
2) ;
;
3)
 ;
4)
;
4)

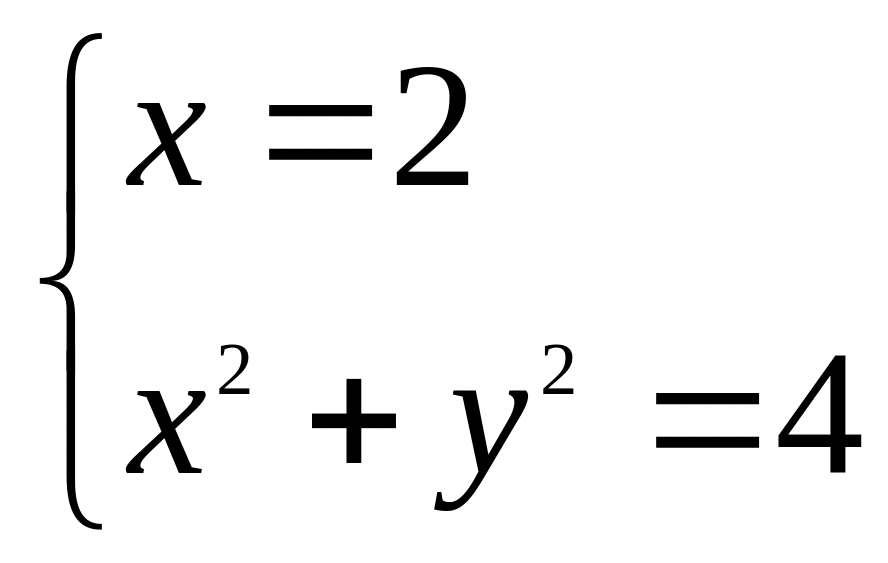 ;
; ;
;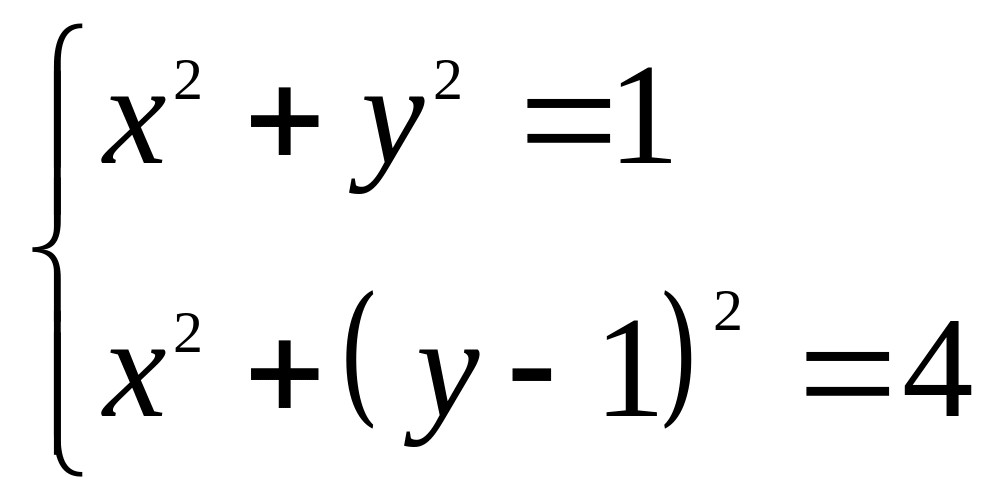 .
.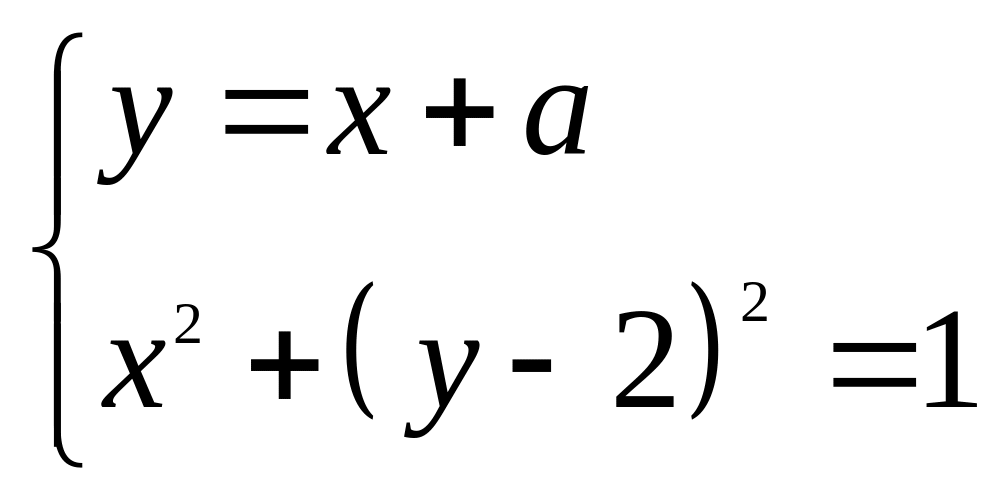 ;
;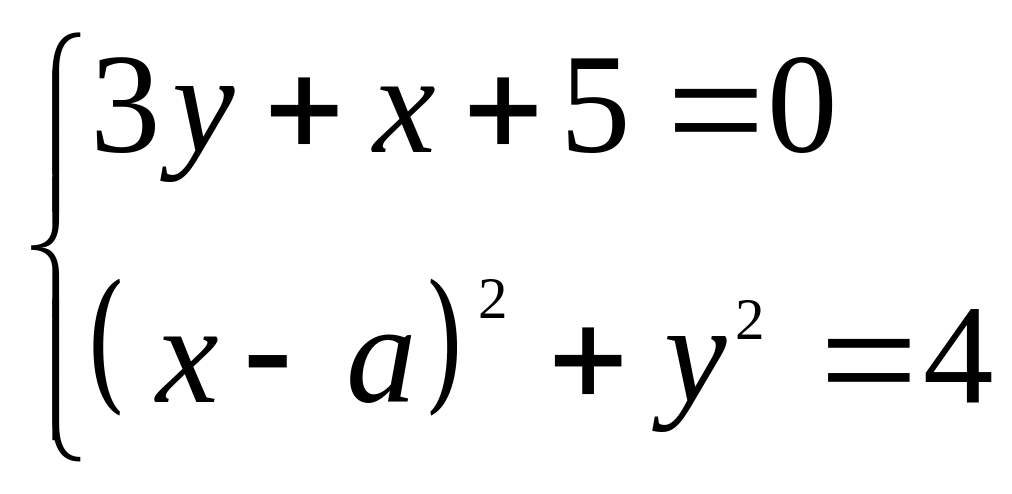 ;
; ;
;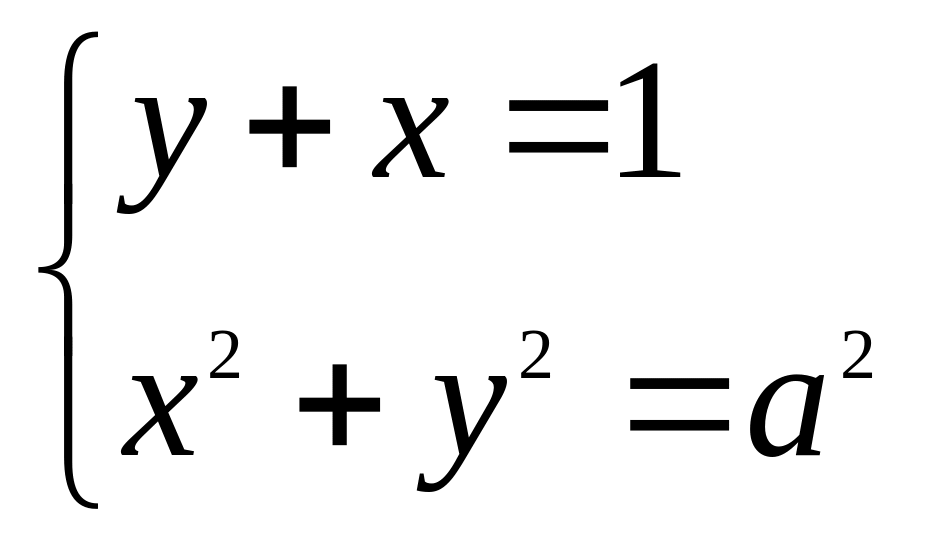 .
.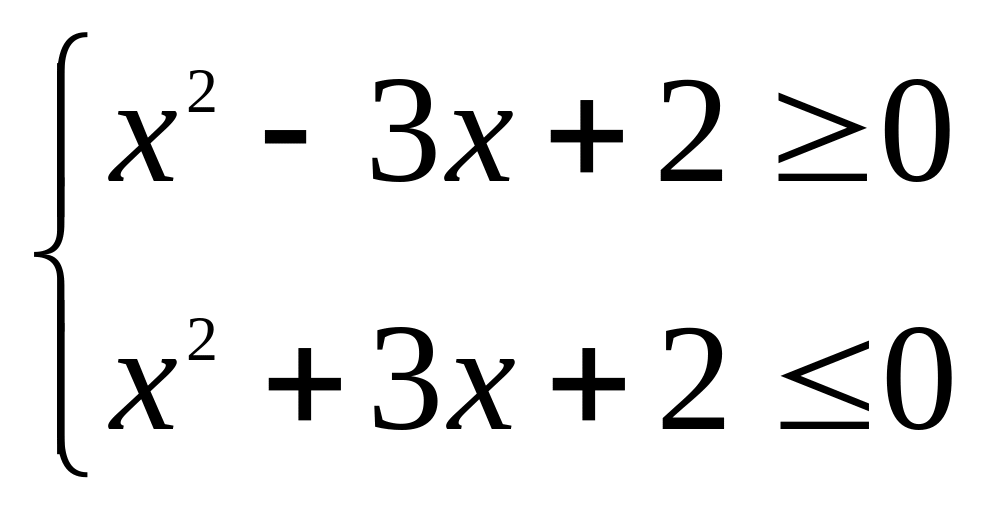 ;
;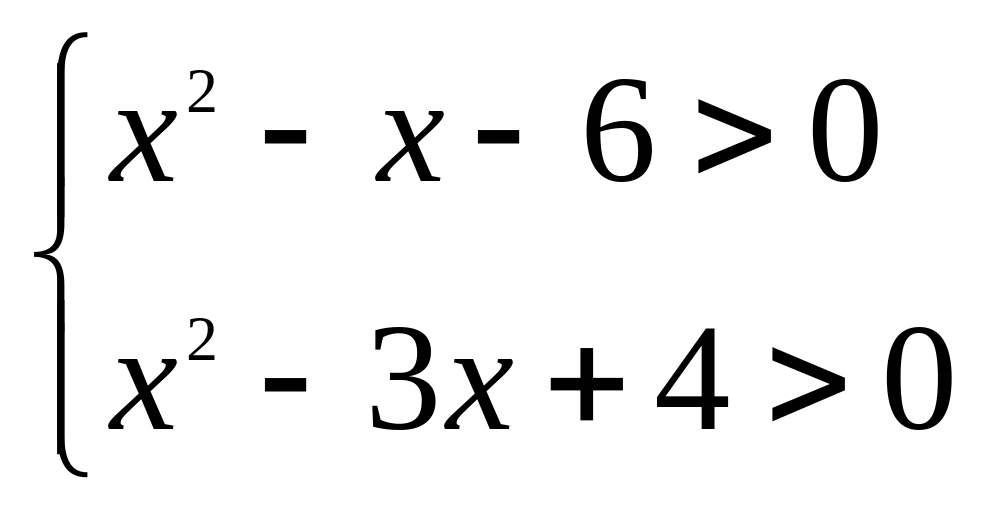 ;
;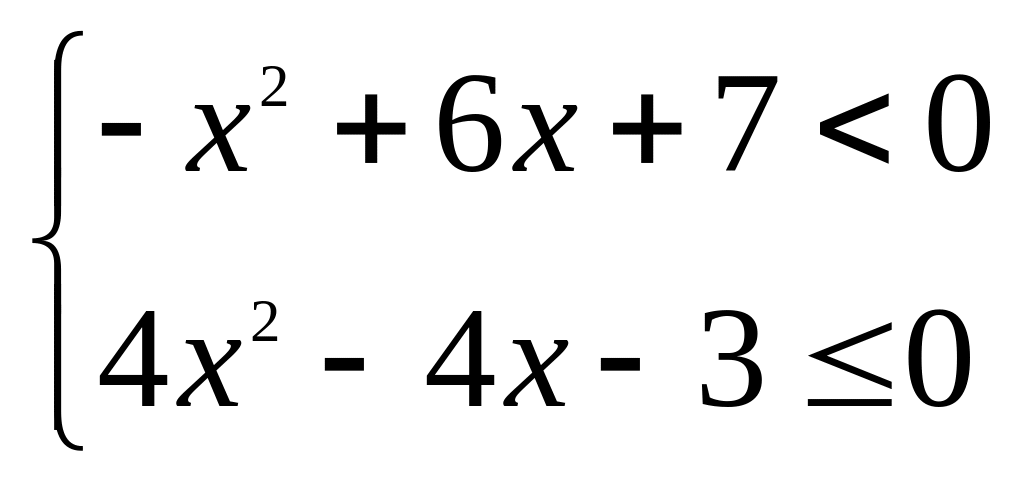 ;
;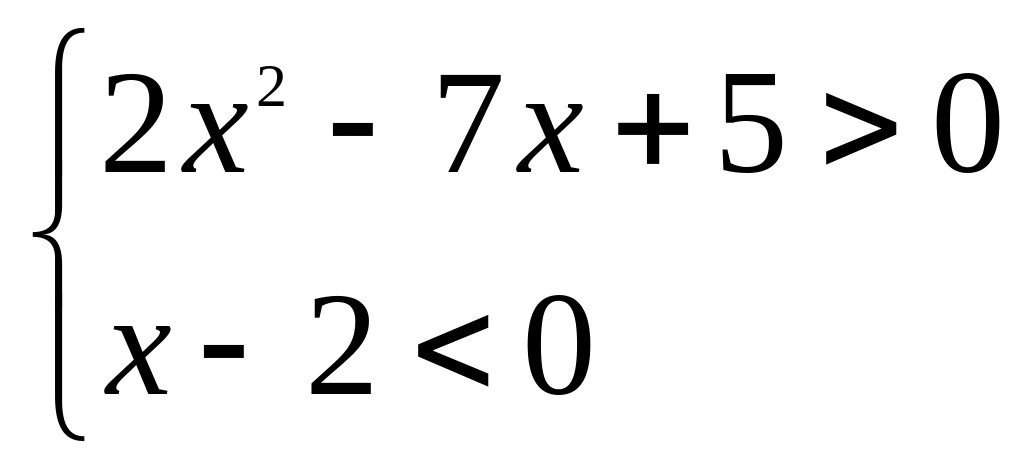 .
.