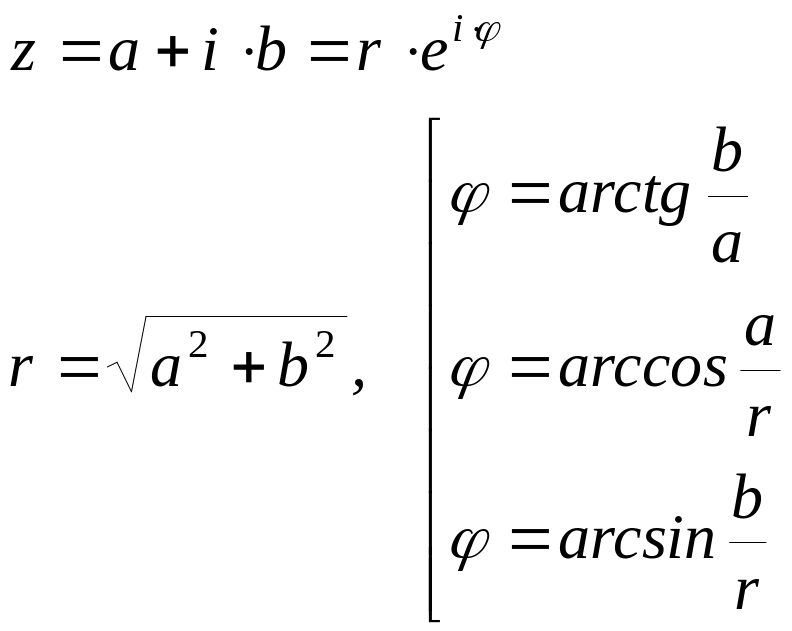- •Алгебраическая форма комплексного числа.
- •Геометрическое изображение комплексных чисел.
- •Тригонометрическая форма комплексного числа.
- •Основные действия над комплексными числами в алгебраической форме.
- •Основные действия над комплексными числами в тригонометрической форме.
- •Возведение комплексного числа в степень и извлечение корня n-ой степени из комплексного числа.
- •Комплексные числа
- •Комплексные числа и действия над ними.
Возведение комплексного числа в степень и извлечение корня n-ой степени из комплексного числа.
Возведение комплексного числа в целую положительную степень Формула Муавра
в алгебраической форме zn=(а+i·b)n – по формулам сокращенного умножения;
в тригонометрической форме [r(cos+isin)]n=rn(cosn+isinn).
при возведении комплексного числа (в тригонометрической форме) в целую положительную степень модуль возводится в эту степень, а аргумент умножается на показатель степени.
Извлечение корня n-ой из комплексного числа
в алгебраической форме не представляется возможным;
в тригонометрической форме
Определение: Корнем п-й степени из комплексного числа называется такое комплексное число, п-я степень которого равняется подкоренному числу, т. е.

Придавая k значения 0, 1, 2, ..., n-1, получим n различных значений корня. Для других значений k аргументы будут отличаться от полученных на число, кратное 2, и, следовательно, получатся значения корня, совпадающие с рассмотренными.
Итак, корень n-й степени из комплексного числа имеет n различных значений.
Корень n-й степени из действительного числа А, отличного от нуля, также имеет п значений, так как действительное число является частным случаем комплексного и может быть представлено в тригонометрической форме:
A=|A|(cos0+isin0) при А>0,
A=|A|(cos+isin) при А<0.
Например: Вычислить все корни третьей степени из комплексного числа z=-3-3i.

Например: Вычислить все корни второй степени из комплексного числа z=-9.

Комплексные числа

b=0 a=0





















Комплексные числа и действия над ними.
|
В алгебраической форме: z1=а1+i·b1; z2=а2+i·b2; |
В тригонометрической форме: z1=r1·(cos1+i·sin1); z2=r2·(cos2+i·sin2); |
В показательной форме: z1=r1·еi·1; z2=r2·еi·2; |
− |
|
|
|
Сложение |
z1+z2=(а1+а2)+i·(b1+b2) |
− |
− |
Вычитание |
z1-z2=(а1-а2)+i·(b1-b2) |
− |
− |
Умножение |
z1z2=(а1а2-b1b2)+i(а2b1+a1b2) |
z1·z2=r1·r2·[cos(1+2)+i·sin(1+2)] |
z1z2=r1·r2·еi·(1+2) |
Деление |
|
|
|
Возведение в степень |
zn=(а+i·b)n – по формулам сокращенного умножения |
[r·(cos+i·sin)]n=rn·(cos n·+i·sinn·) |
[r·еi·]n=rn·еi··n |
Извлечение корня |
− |
k=0, 1, 2, n-1. |
k=0, 1, 2, n-1. |