14 лекция Первообразная и неопределённый интегр

Раздел 2. Интегральное исчисление.

Дифференциальные уравнения. Ряды.

Тема 5. Интегралы.

Лекция 14. Первообразная и неопределённый интеграл.

65. Первообразная

Восстановление функции по известной производной этой функции составляет одну из основных задач интегрального исчисления.

Определение 1: Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений х из этого промежутка выполняется равенство F(x)=f(x).

Задача отыскания по данной функции f(x) её первообразной решается неоднозначно. Действительно, если F(x) — первообразная для f(x), т. е. F(x)=f(x), то функция F(x)+C, где С—произвольная постоянная, также является первообразной для f(x), так как [F(x)+C]=f(x) для любого числа С.

Теорема 1: Функция, производная которой на некотором промежутке X равна нулю, постоянна на этом промежутке.

Теорема 2: Если F(x) — первообразная для функции f(x) на некотором промежутке X, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x)+C, где С— произвольная постоянная.

65. Неопределённый интеграл.

Определение 1: Если функция F(x) — первообразная для функции f(x), то множество функций F(x)+C, где С — произвольная постоянная, называется неопределённым интегралом от функции f(x) и обозначается символом

При этом функция f(x) называется подынтегральной функцией, f(x)dx—подынтегральным выражением, а переменная х — переменной интегрирования.

Символ обозначает, таким образом, совокупность всех первообразных для функции f(x).

Восстановление функции по ее производной или, что то же, отыскание неопределённого интеграла по данной подынтегральной функции называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.

В связи с понятием первообразной возникает вопрос: для каких функций существуют первообразные (а значит, и неопределённые интегралы).

Доказано любая непрерывная на отрезке функция имеет на этом отрезке первообразную (следовательно, и неопределённый интеграл). В дальнейшем будем считать, что все функции, стоящие под знаком интеграла, непрерывны и формула имеет смысл.

В случае разрывной функции будем рассматривать ее интегрирование только в тех промежутках, в которых она непрерывна.

Геометрически неопределенный интеграл представляет собой множество (семейство) кривых, являющихся графиками первообразных y=F(x)+С. Если y=F(x) - какая-нибудь кривая, то все другие кривые получаются из неё параллельным сдвигом вдоль оси Оу.

65. Свойства неопределённого интеграла.

Свойство 1: Производная неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению, т. е.

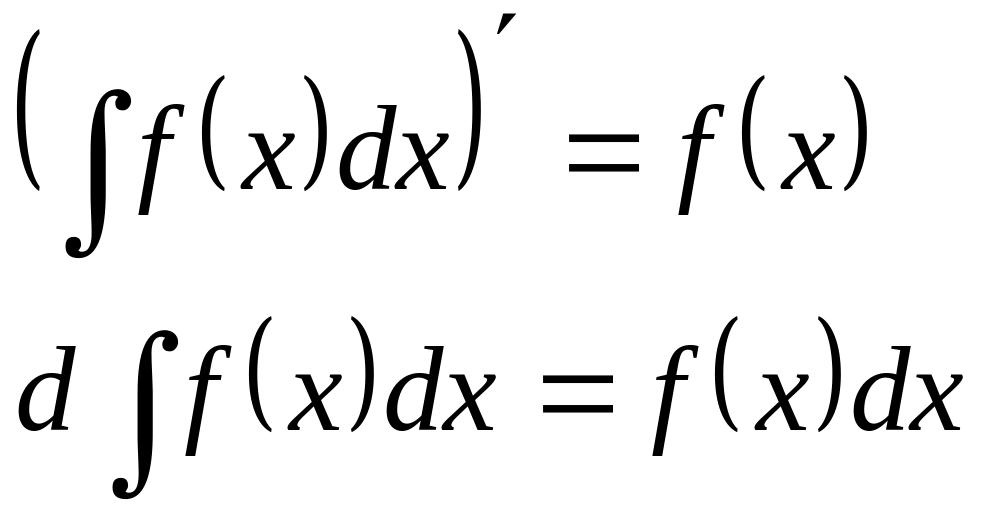
Свойство 2: Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т. е.

Свойство 3: Постоянный множитель можно вынести из-под знака интеграла, т. е. если k=const0,

Свойство 4: Неопределённый интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно, т. е.

.

65. Основные методы интегрирования.

1. Непосредственное интегрирование;

2. Метод подстановки;

3. Метод интегрирования по частям.

1. Непосредственное интегрирование. Вычисление интегралов с помощью таблицы простейших интегралов и основных свойств неопределённых интегралов называется непосредственным интегрированием.

2. Метод подстановки. Во многих случаях введе­ние новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного, т. е. перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной. В его основе лежит следующая теорема.

Теорема: Пусть функция x=(t) определена и дифференцируема на некотором промежутке Т и пусть X - множество значений этой функции, на котором определена функция f(x), т. е. на Т определена сложная функция f((t)). Тогда если на множестве X функция f(x) имеет первообразную F(x), то справедлива формула (формула замены переменной в неопределённом интеграле):

Тождественное преобразование подынтегрального выражения с выделением дифференциала новой переменной интегрирования – простейшая замена переменной или метод внесения под знак дифференциала. Таким образом, устанавливается и общая формула

3. Метод интегрирования по частям. Метод ин­тегрирования по частям основан на использова­нии формулы дифференцирования произведения двух функций.

Теорема: Пусть функции u(х) и v(x) определены и дифференцируемы на некотором промежутке X и пусть функция u'(x)v(x) имеет первообразную на этом промежутке, т. е. существует v(x)u'(x)dx. Тогда на промежутке X функция u(x)v'(x) также имеет первообразную и справедлива формула:

Интегрирование сложнее дифференцирования. Дифференцирование не выводит из класса элементарных функций в отличие от интегрирования.

Таблица неопределённых интегралов некоторых функций.

Основные свойства неопределённого интеграла.

	Производная неопределённого интеграла равна подынтегральной функции.
	Дифференциал от неопределённого интеграла равен подынтегральному выражению.
	Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной.
	Постоянный множитель можно вынести из-под знака интеграла, если k=const0.
	Неопределённый интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно.

Связь между дифференцированием и интегрированием:

Простейшая функция	Дифференциал	Интеграл

Основные методы интегрирования.

Непосредственное интегрирование	Вычисление интегралов с помощью таблицы простейших интегралов и основных свойств неопределённых интегралов.
Метод подстановки (метод замены переменной)	Введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного, т. е. перейти к непосредственному интегрированию: или
Метод интегрирования по частям	Основан на использовании формулы дифференцирования произведения двух функций:

Основные свойства определённого интеграла.

Если а=b, то	Если а>b, то
	Каковы бы ни были числа а, b и с, всегда имеет место это равенство
	Постоянный множитель можно выносить за знак определённого интеграла.
	Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов.
Если всюду на отрезке [а, b] функция f(x)0, то	Если всюду на отрезке [а, b] функция f(x)g(x), то

Формула Ньютона Лейбница.

Замена переменной в определённом интеграле:

Интегрирование по частям в определённом интеграле:

3