Номограма поправок

Наведемо приклад опрацювання однієї з найдовших сторін в полігонометричному ході 1 розряду

,

з графіка для 3-х метрів; С=+10мм –з таблиці.

Визначаємо по номограмі за температурою і тиском на 100 м; з графіку, що знаходиться в паспорті .

Підставимо всі поправки у формулу обчислення віддалі

Для переходу до горизонтальної проекції вноситься поправка за перевищення відбивача та приладу - , або ,

;

Горизонтальна проекція виміряної лінії буде дорівнювати

1313208-1,6=1313206,4мм,

або через кут нахилу .

мм.

Державна і розрядна полігонометрія вимагає внесення ще двох поправок: за перехід на референт - еліпсоїд та за перехід на площину Гаусса – Крюгера

В цих обчисленнях бажано скористатись посібником авторів Бугаева, Гричука, Ярового «Таблицы для вычисления длин сторон полигонометрии и трилатерации 1 и 2 классов измеренных свето и радиодальномером »1969.

1. Поправка за перехід на референц – еліпсоїд

В горизонтальні проекції виміряних ліній вводяться поправки за перехід на референц- еліпсоїд за формулою (першого порядку):

де - середня висота лінії над рівнем моря ;

радіус кривизни земного еліпсоїду в точці , що лежить посередині лінії. Визначається з Таблиць за функцією широти точки ( ) і азимуту лінії знятих з карти.

лінія приведена до горизонту.

Підставимо аргументи у виміряну лінію :

2. Поправка за перехід на площину в проекції Гаусса – Крюгера

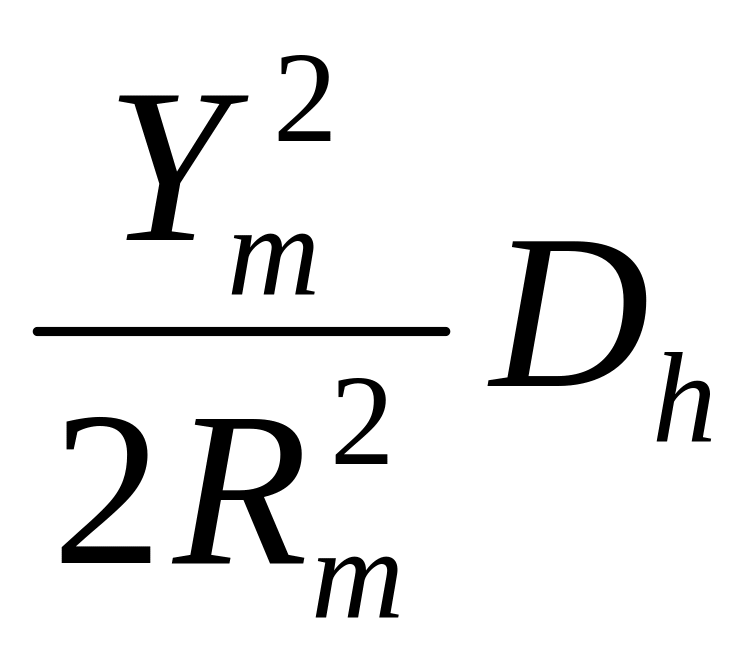
де віддаль точки m, на середині лінії, від осьового меридіана.

Віддаль може бути додатною і від’ємною, але в формулі вона в другій степені , величина поправки завжди буде додатною.

В прикладі , віддаль точки m від осьового меридіану -448,1км в 6°зоні.

Поправка в міліметрах буде

.

Сумуючи одержані поправки будемо мати приведену довжину ліній ,що братимуть участь в наступних зрівнюваннях строгим методом з умовними рівняннями і вільними членами. Якщо метою є обчислення наближених координат пунктів без зрівнювання, обчислення виконуються за схемою теодолітного ходу ,але оперують з секундами і міліметрами. Результати порівнюють з вимогами до полігонометрії.

Обчислення кутової нев’язки ходу та порівняння її з допустимим значенням.

Кутова нев’язка розімкнутого ходу з виміряними лівими по ходу кутами обчислюється за формулою

Для замкнутого ходу і внутрішніх кутів нев’язку знаходять за формулою

Отримані нев’язки порівнюють з допустимими значеннями встановленими Інструкцією.

Для полігонометрії 1 розряду ,наприклад,

Якщо кутова нев’язка менша за допустиму то обчислювальні роботи продовжують. Для обчислення наближених координат пунктів одержану нев’язку розподіляють як поправку ,змінивши знак , порівну в усі виміряні кути.

Обчислення приростів координат та їх нев’язок і порівняння їх з допустимими значеннями.

За виправленими кутами обчислюють дирекційні кути сторін

Тобто: дирекцій ний кут наступної лінії дорівнює дирекційному кутові попередньої лінії плюс лівий за ходом кут мінус 180 . Бувають випадки, коли обчислений дирекційний кут може мати значення більше за 360 то такий дирекційний кут необхідно зменшити на 360

Прирости координат обчислюють за формулами

.

Нев’язки в координатах, у розімкнутих ходах, за формулами

і якщо хід замкнутий

За нев’язками в приростах координат обчислюють абсолютну лінійну нев’язку

а на практиці користуються відносною нев’язкою ,тобто відношенням до периметра ходу ( )

Допустимі відносні нев’язки для всіх класів і розрядів приведені в Інструкції. Для полігонометрії 1розряду 1: 10000. Якщо наша відносна нев’язка менша або дорівнює допустимій роблять висновок, що хід виконано за необхідними технічними вимогами . Нев’язки в приростах координат розподіляють по приростах пропорційно до довжин ліній з протилежним знаком так , щоб після розподілу нев’язок суми приростів координат дорівнювали нулю, для замкнутого ходу; для розімкнутого- щоб були одинакові виправлені практичні і теоретичні суми приростів, одержані як різниці координат кінцевої і початкової точок.. Розподілити нев’язки на всі лінії можна за такими формулами:

В полігонометрії нев’язки малі і тому вираховують їх не на 1м довжини, а на 100 м. Додаючи алгебраїчно обчислені поправки до обчислених приростів координат одержують виправлені прирости координат. Після цього знаходять координати пунктів полігонометричного ходу за правилом: координата наступної точки дорівнює координаті попередньої плюс приріст координат.

Кінцеві координати X , Y контролюють правильність обчислення координат кінцевої точки .