2. Внутрішня енергія ідеального газу.

Використаємо отримані співвідношення для ідеального газу. В цьому випадку термічне рівняння являє собою закон Клапейрона-Менделєєва, який для одного моля запишемо

А Колоритне рівняння можна отримати, використовуючи досліди Гей-Люссака та Джоуля-Томсона.

Д ві мідні посудини з однакових об’ємами були з’єднані трубою із краном С. Посудина А була наповнена повітрям, а з В повітря відкачали. При відкриванні крану С повітря з А прямувало в В. При цьому температура в А дещо понижалась, а в В – збільшувалась. Така зміна температури пояснюється тим, що повітря в А при розширені виконувало роботу за рахунок внутрішньої енергії. При досягненні стану термодинамічної рівноваги в А і В встановлювалась температура, рівна початковій.

Проаналізуємо експеримент. Газ знаходиться в жорсткій оболонці, тому зовнішня робота не виконувалась. Кількістю теплоти, що надходила із зовні за час досліду, можна знехтувати. Тому внутрішня енергія повітря повинна залишатись незмінною. Дослід показав, що температура газу залишилась незміною, в той час як об’єм збільшився вдвічі. Звідси можна зробити висновок, що внутрішня енергія газу не залежить від об’єму.

Джоуль повторив дослід в дещо зміненій формі. Повітря в посудині знаходилось під тиском 22 атм. Посудини занурювались у воду, яка переміщувалась під час досліду, щоб температура залишалась всюди постійною. При відкриванні крану С повітря перетікало з А в В, але зміни температури не спостерігались.

Отже для ідеального газу

.

Дослід показує, що у одноатомних газів не залежить від , для інших ідеальних газів існує слабка залежність від температури. Якщо , то ми одразу отримуємо калоричне рівняння

.

3. Рівняння Роберта Майєра

О скільки внутрішня енергія ідеального газу не залежить від об’єму , враховуючи рівняння Клапейрона-Менделєєва (яке дає ), для ідеального газу формулу (9) можна записати

. (10)

Дане співвідношення, яке пов’язує молярні теплоємності і ідеального газу, називається рівнянням Роберта Майєра.

Розділивши (10) на масу одного моля, отримаємо рівняння Майєра для питомих теплоємностей

. (11)

С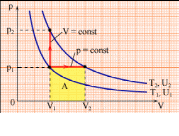 піввідношення Майєра (10) можна пояснити таким чином. На рисунку приведені ізобарний і ізохорний процеси нагрівання газу на . Якщо об’єм постійний, то теплота йде на підвищення температури на , і новий тиск дорівнює . Якщо дати газу можливість розширятися, то (тиск залишається постійним ) газ стане розширюватись і охолоджуватись за рахунок здійснення роботи. Тобто нагрівання в цьому випадку менше, ніж нагрівання при постійному об’ємі . Тому, щоб нагрівання в процесі при постійному тиску було таким же, необхідно додати більшу теплоту.

Таким чином, універсальна газова стала , числено дорівнює роботі, яку виконує 1 моль ідеального газу, розширюючись при нагріванні на 1 К.

4. Політропічні процеси

Рівняння ізотермічного, ізохорного, ізобарного процесів для ідеального газу ми отримали, виходячи лише з рівняння стану ідеального газу. Рівняння ж адіабатного і політропного (із постійною С) процесів не можна отримати, використовуючи лише термічне рівняння, оскільки останнє не включає ані кількість теплоти , ані теплоємність С, які визначають ці процеси. Знайдемо ці рівняння, виходячи з першого закону термодинаміки. При політропічному процесі і (для адіабатного процесу ). Тому для політропи з першого початку термодинаміки маємо

. (12)

Звідки, враховуючи (9),

. (13)

Це диференціальне рівняння політропи в змінних і .

Щоб перейти до змінних р і можна із рівняння стану, записаного у вигляді , знайти

і підставити у попереднє рівняння.

Для того, щоб про інтегрувати рівняння (13), необхідно знати не тільки зв'язок між , р і але і вирази для і .

Давайте розглянемо випадок ідеального газу. Введемо позначення

- показник політропи (14)

- показник адіабати (14`)

Для ідеального газу і для широкого інтервалу температур не залежить від температури, тому n і не залежать від температури.

Оскільки , то (13) перепишеться (врахуємо також )

.

Яке інтегрується

- рівняння політропічного процесу (15)

- адіабати. (15`)

С користавшись рівнянням стану , перепишемо (15) і (15`)

(16)

- рівняння Пуасона (16`)

і з (15`) випливає, що при адіабатичному стисненні газ нагрівається. Це явище використовується в дизелях, де горюча суміш загорається при адіабатичному стиснені (див. 7 стор. 76).

Порівнюючи рівняння Пуассона з рівнянням Бойля-Мариотта , можна переконатися, що адіабата ідеального газу, побудована в координатах p і V, завжди йде крутіше ізотерми.

Це пояснюється тим, що при адіабатному процесі відбувається охолодження газу, в той час як в ізотермічному процесі температура підтримується постійною. Тому при ізотермічному розширенні тиск газу зменшується тільки за рахунок зменшення густини газу, а при адіабатному – за рахунок зменшення густини і середньої кінетичної енергії, тобто температури.

Оскільки адіабата перетинає всі ізотерми даної термодинамічної системи, можливий адіабатичний перехід з однієї ізотерми на іншу, шляхом стискування або розширення газу. А за допомогою ізотермічної зміни об'єму можливий перехід з однієї адіабати на іншу.