7.4. Поля в аффинном пространстве. Локальный базис

Функция, заданная на области M аффинного пространства называется полем. Конечно, точки MÎM могут быть представлены своими декартовыми или криволинейными координатами. Значениями данной функции могут быть скаляры (скалярное поле), векторы (векторное поле), тензоры из (тензорное поле).

Операции над тензорными полями одного ранга (только скалярными, только векторными, и т. д.) и композиции тензорных полей, заданные на одной и той же области аффинного пространства выполняются поточечно. Все, что в предыдущих главах относилось к тензорам, естественным образом переносится на тензорные поля и имеет место в тензорном пространстве значений поля в каждой точке аффинного пространства.

В теории упругости механики сплошной среды для каждой точки деформируемого тела, занимающего область трехмерного аффинного пространства, определены тензоры напряжений и деформаций, а также тензорная функция, их связывающая.

В частном случае векторного поля в векторном пространстве значений поля можно определить особый базис, связанный с системой координат в аффинном пространстве и зависящий от точки поля (т.е. локальный). Введем этот базис.

Рассмотрим координатные линии некоторой криволинейной системы координат, проходящие через некоторую точку M с координатами . Согласно (7.13¢) уравнение координатной линии имеет вид

.

Требование (7.6) позволяет нам взять производную от этой векторной функции по в точке M (векторы репера от не зависят), что даст в результате вектор , касательный к координатной линии

(рис. 7.4).

Рис. 7.4. Смысл вектора локального базиса

Для произвольной координатной линии

(7.14)

В декартовой системе координат , и выражение (7.14) принимает вид

. (7.15)

Условимся считать в выражениях вида индекс j нижним. В рамках данного соглашения иногда пользуются краткой записью . Это соглашение эквивалентно определению (7.14), согласно которому векторы считаются векторами основного базиса, а компоненты — компонентами разложения в базисе , .

Векторы являются линейно независимыми. Это следует из того, что определитель, составленный из компонент разложения по базису в (7.14) всегда отличен от нуля (условие (7.7)). Следовательно, векторы образуют базис в . Этот базис, состоящий из векторов , касательных к координатным линиям в данной точке пространства , называется локальным базисом.

Для произвольной системы координат векторы локального базиса различны в различных точках пространства . Исключением является декартова система координат, в которой все локальные базисы совпадают с реперными векторами. Существование такой системы координат в аффинном пространстве делает возможным отождествить векторные пространства значений векторного поля в различных точках M Í .

Если векторы локального базиса в какой-либо точке области образуют правую тройку, то и в других точках этой области тройка локальных базисных векторов всегда будет правой (предлагаем убедиться в этом), и такую систему координат можно назвать правой. Конечно, подобный вывод справедлив и для левой системы координат.

Рассмотрим закон преобразования векторов локального базиса при преобразовании систем координат. Пусть имеются две системы координат — “старая” и “новая” . Соответствующие векторы локального базиса определяются выражениями

. (7.16)

Тогда связь между и может быть установлена соотношениями

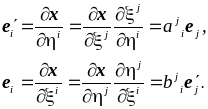(7.17)

матрицы преобразования и в (7.17) являются невырожденными и взаимно обратными, что следует из (7.7).

Кроме алгебраических операций, в предположении достаточной гладкости тензорного поля над ним определяется операция ковариантного дифференцирования. Рассмотрим сначала векторное поле

. (7.18)

Явная запись аргументов в (7.18) подчеркивает, что значение векторного поля t в данной точке задано компонентами в локальном базисе e_i. Полагая поле (7.18) дважды дифференцируемым, рассмотрим производную

. (7.19)

Производная базисного вектора по криволинейным координатам , найденная в каждой точке области аффинного пространства, есть векторное поле. В каждой рассматриваемой точке разложим эту производную по векторам локального базиса

(7.20)

(желательно запомнить закономерность в расположении индексов справа и слева).

Компоненты разложения вектора в локальном базисе e_i называются символами Кристоффеля II рода. Подставляя (7.20) в (7.19) получим

. (7.21)

Выражение в скобках называют ковариантной производной контравариантных компонент вектора. Кроме частной производной данных компонент в ковариантную производную входят компоненты частных производных векторов локального базиса.

В аффинном пространстве ранее введенный локальный базис следует считать основным базисом.