Плоскость и прямая в пространстве Рассмотрим геометрические объекты, которые описываются линейными алгебраическими уравнениями.

Плоскость P в декартовой прямоугольной системе координат может быть задана одним из уравнений:

1) – общее уравнение плоскости;

2) – уравнение плоскости, проходящей через точку перпендикулярно нормальному

вектору ;

3) 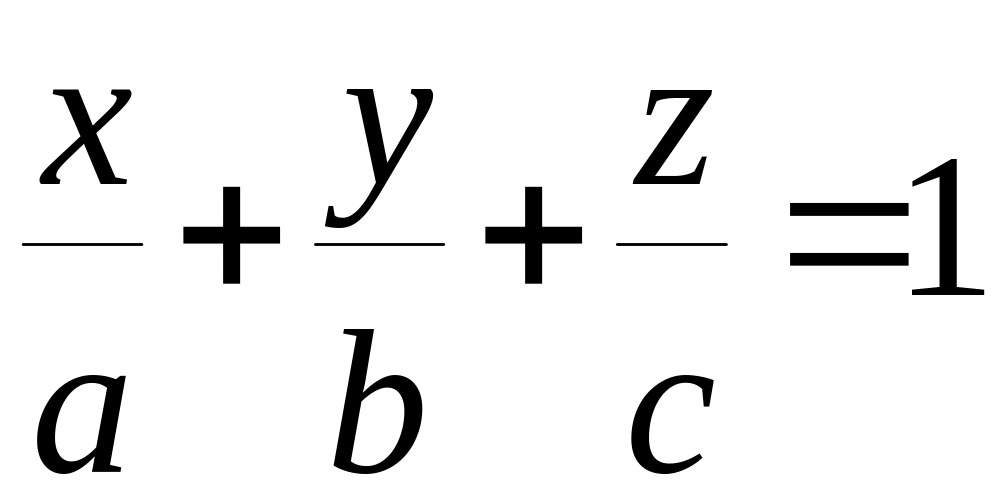- уравнение плоскости в отрезках, где – величины направленных отрезков, отсекаемых плоскостью на координатных осях соответственно;

4) Уравнение плоскости, проходящей через три заданные точки , не лежащие на одной прямой, можно записать в виде

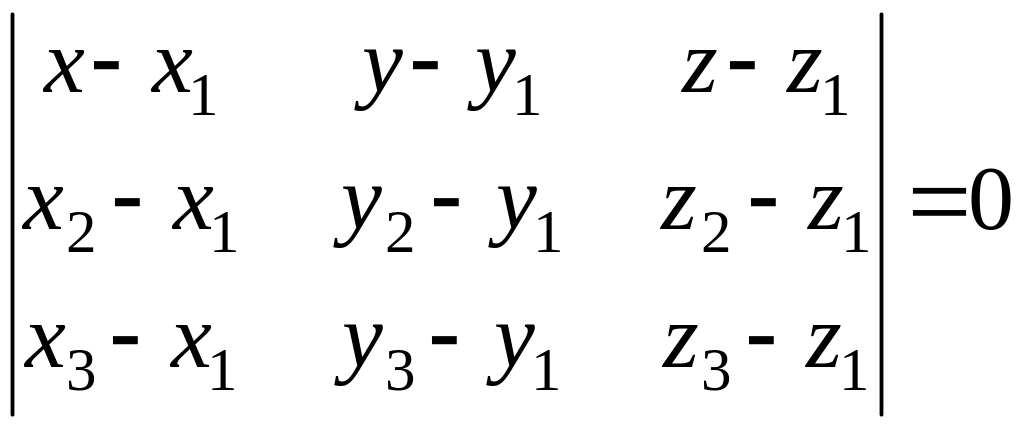или ;

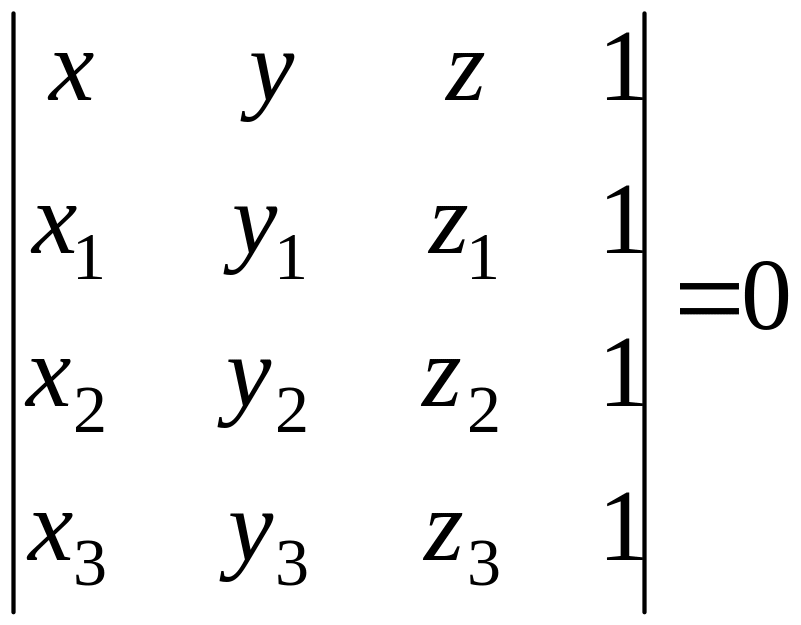5) – нормальное уравнение плоскости, где направляющие косинусы вектора , перпендикулярного плоскости; – расстояние от начала координат до плоскости.

Анализируя все перечисленные уравнения плоскости, приходим к выводу: всякое уравнение первой степени относительно координат точки пространства изображает плоскость, и, наоборот, всякая плоскость может быть представлена уравнением первой степени, содержащим три независимых параметра.

Если в указанном уравнении отсутствует свободный член , то плоскость проходит через начало координат. Если отсутствует член с одной из координат , то плоскость параллельна соответствующей оси координат; если одновременно отсутствуют свободный член и член с одной из координат, то плоскость проходит через соответствующую ось. Если отсутствуют члены с двумя координатами, то плоскость параллельна той координатной плоскости, которая содержит соответствующие оси. Если отсутствуют член уравнения с двумя координатами и свободный член, то плоскость совпадает с одной из координатных плоскостей.

Прямая L в пространстве может быть задана:

1. общими уравнениями

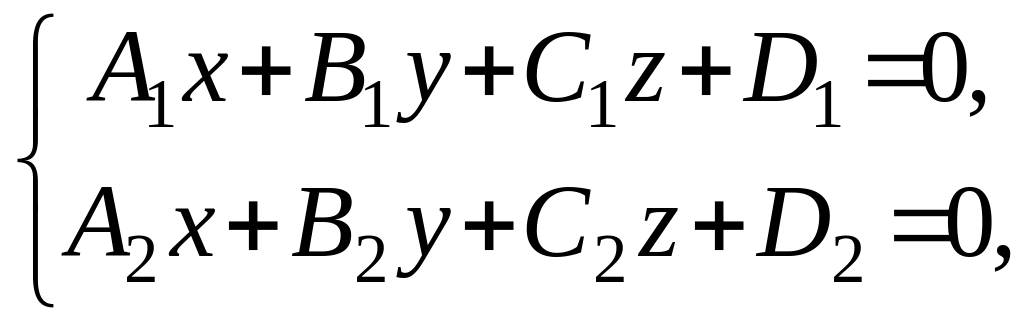
как линия пересечения двух непараллельных плоскостей;

2. каноническими уравнениями

,

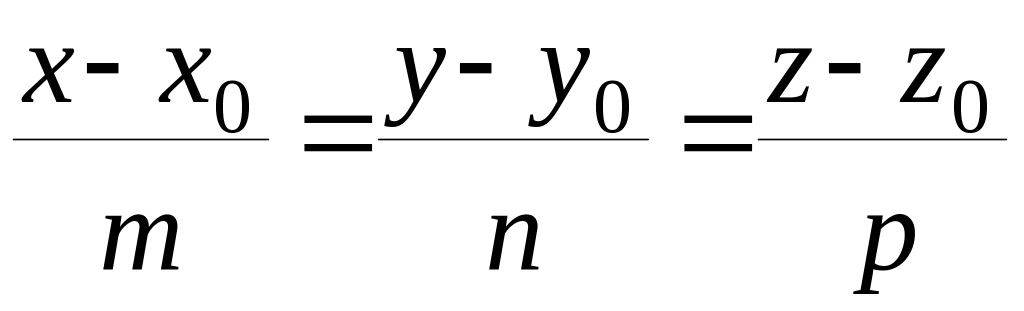как прямая, проходящая через точку параллельно

направляющему вектору ;

3. параметрическими уравнениями

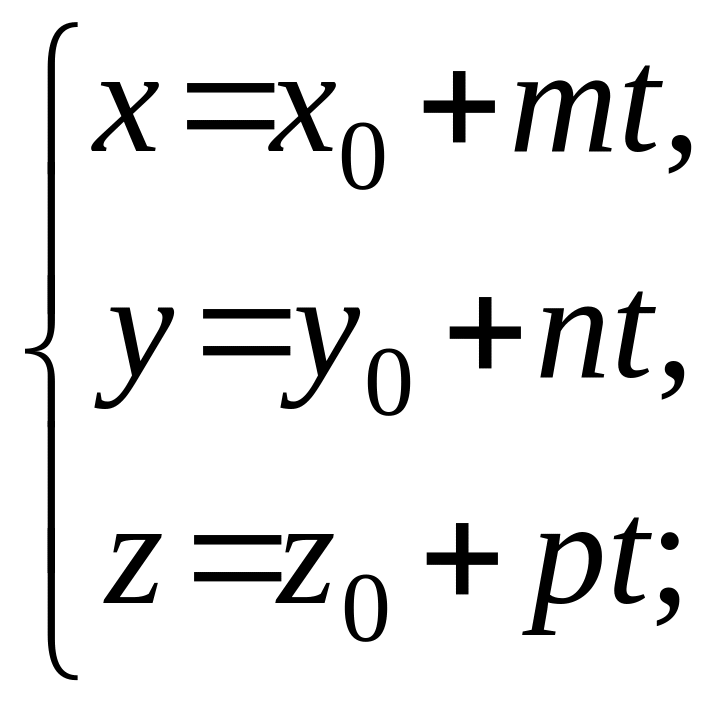
4. уравнениям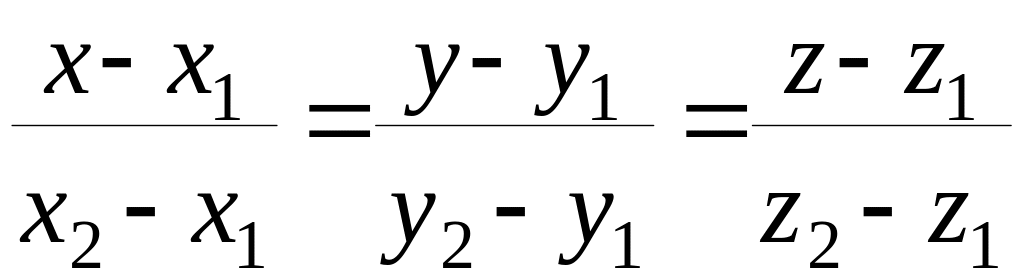и , как прямая, проходящая через две заданные точк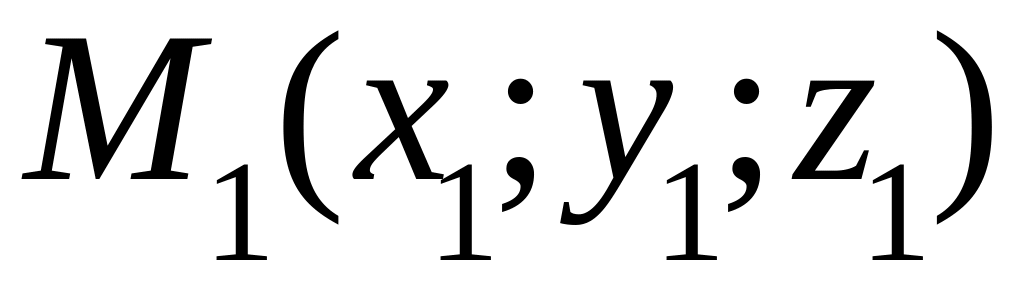и и .

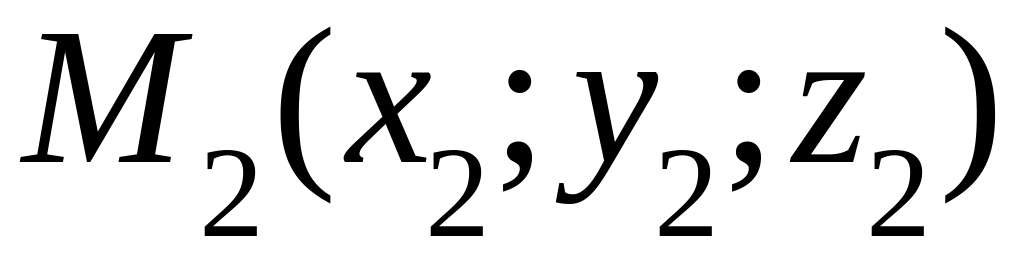Взаимное расположение двух плоскостей, прямой и плоскости, двух прямых в пространстве

Пусть имеем две плоскости

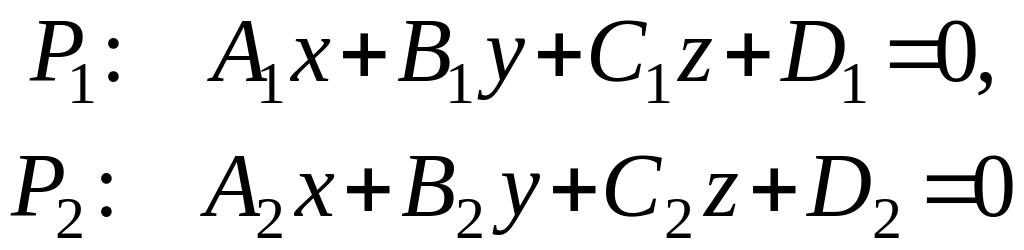
с нормальными векторами и .

Определим угол между плоскостями и их взаимное расположение:

а) Величина угла между плоскостями P₁ и Р₂ вычисляется по формуле .

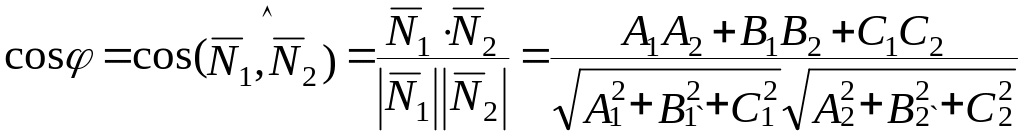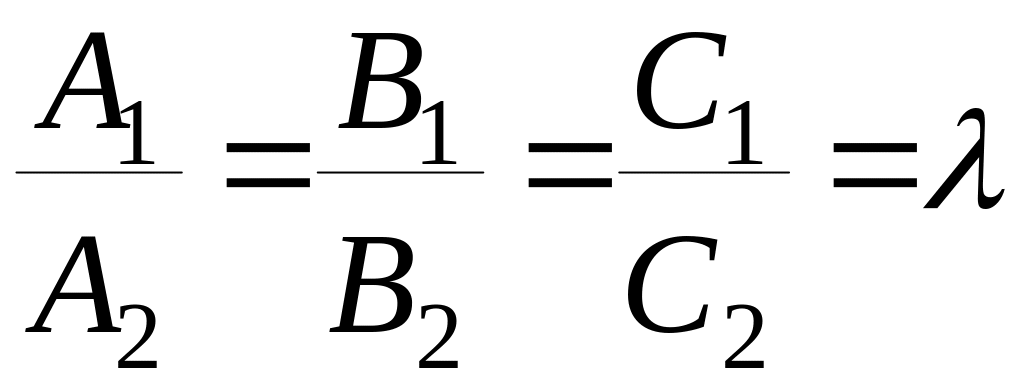б) Плоскости P₁ и Р₂ параллельны (перпендикулярны), если их нормальные векторы коллинеарны (ортогональны): или ;

или .

Расстояние d от точки до плоскости вычисляется по формуле:

.

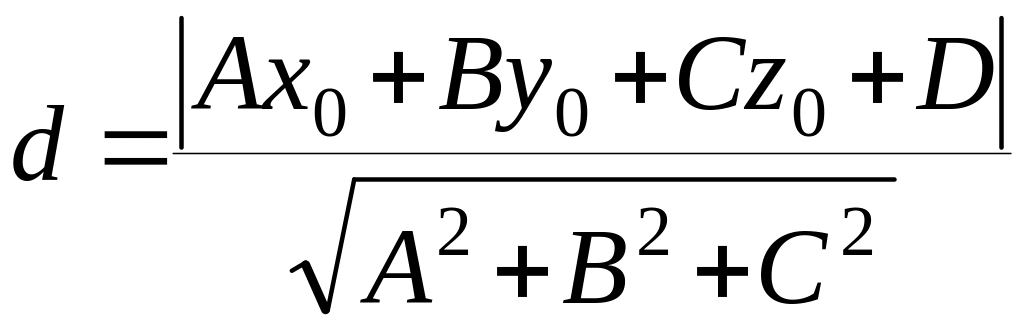Пусть плоскость P задана уравнением , а прямая L уравнениями .

Определим угол между прямой и плоскостью, и их взаимное расположение:

а) Угол между прямой L и плоскостью P, как угол между этой прямой и ортоганальной проекцией ее на плоскость P, вычисляется по формуле .

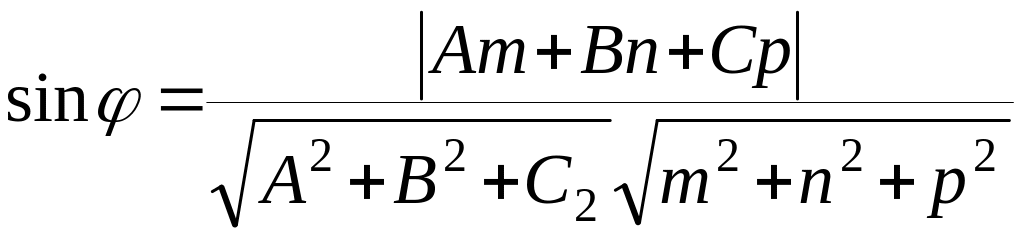б) Условие параллельности прямой и плоскости:

т.е.

в) Условие перпендикулярности прямой к плоскости: , т.е. .

Пусть две прямые L₁ и L₂ заданы уравнениями

, .

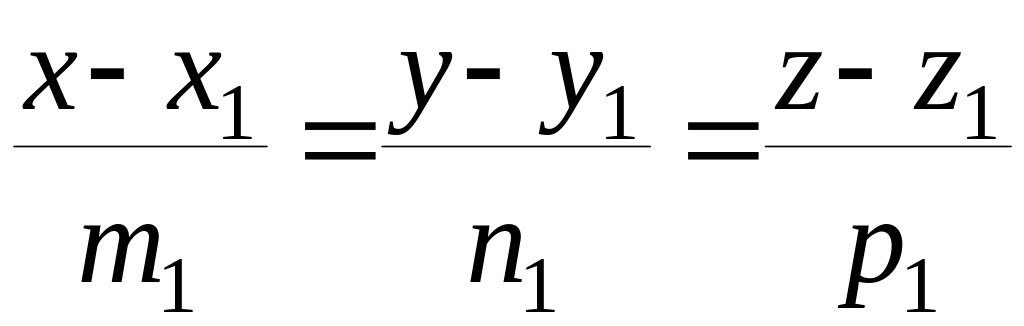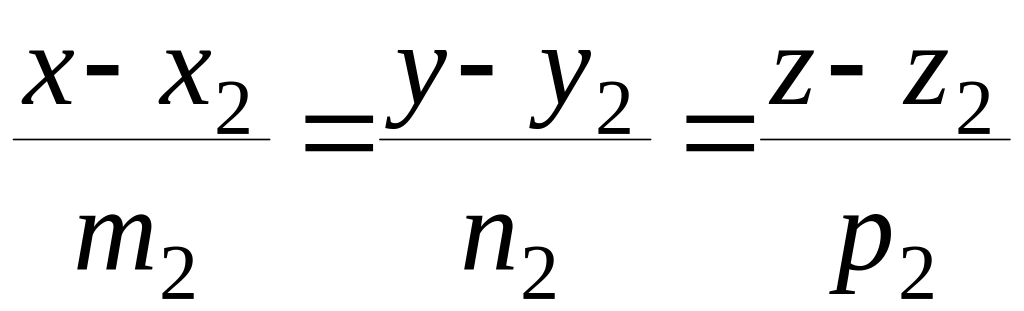Установим их взаимное расположение:

а) Угол между прямыми L₁ и L₂ вычисляется по формуле

.

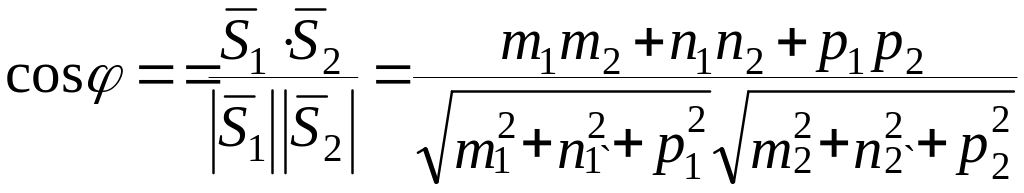б) Условие перпендикулярности двух прямых: т.е. .

в) Условие параллельности двух прямых: , т.е. .
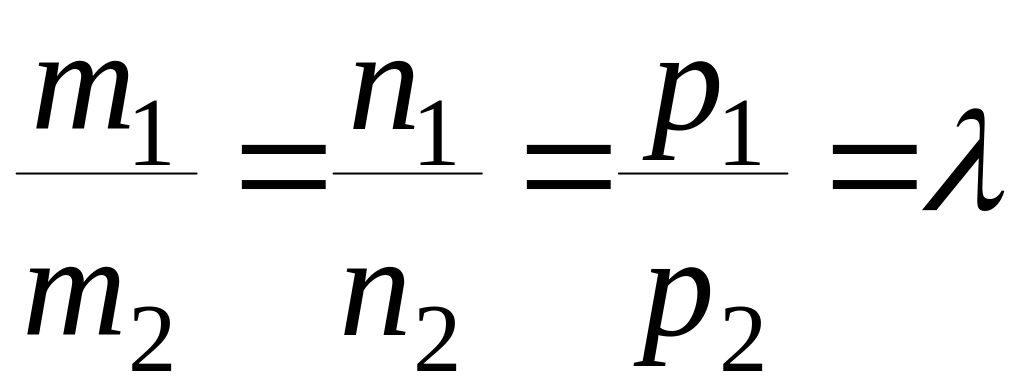