Умножение векторов

Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: , где .

Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел.

Векторным произведением двух векторов и называется вектор , который:

1. имеет модуль, численно равный площади параллелограмма, построенного на векторах и : ;

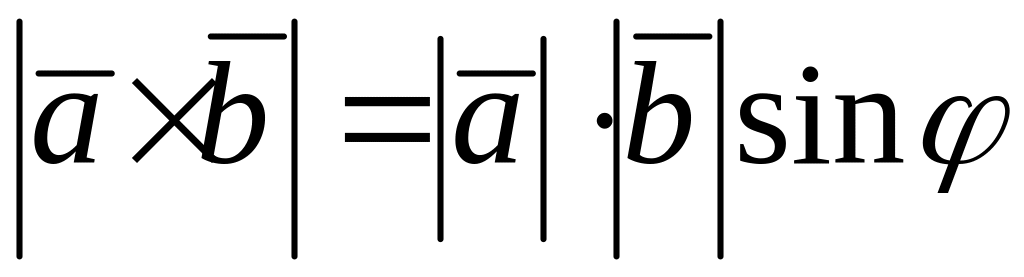2. перпендикулярен к плоскости этого параллелограмма;

3. направлен в такую сторону, с которой кратчайший поворот от к рассматривается совершающимся против часовой стрелки (такое расположение векторов , и 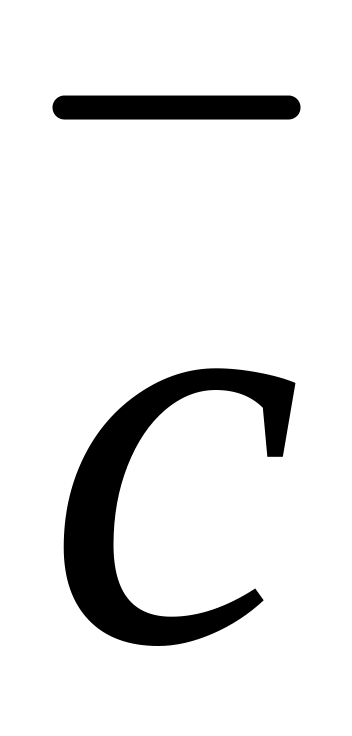называется правой тройкой векторов).

Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: .

Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно.В результате получают число.

Смешанное произведение трех векторов , и , которое обозначается или , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах , и , как на ребрах.

Указанные произведения векторов и их свойства достаточно просто выражаются через их прямоугольные координаты, т.е. координаты векторов в базисе , по сравнению с аналогичными выражениями в произвольном базисе , которых мы не приводим.

Пусть заданы два вектора и .

Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:

.

Угол между векторами вычисляется по формуле

,

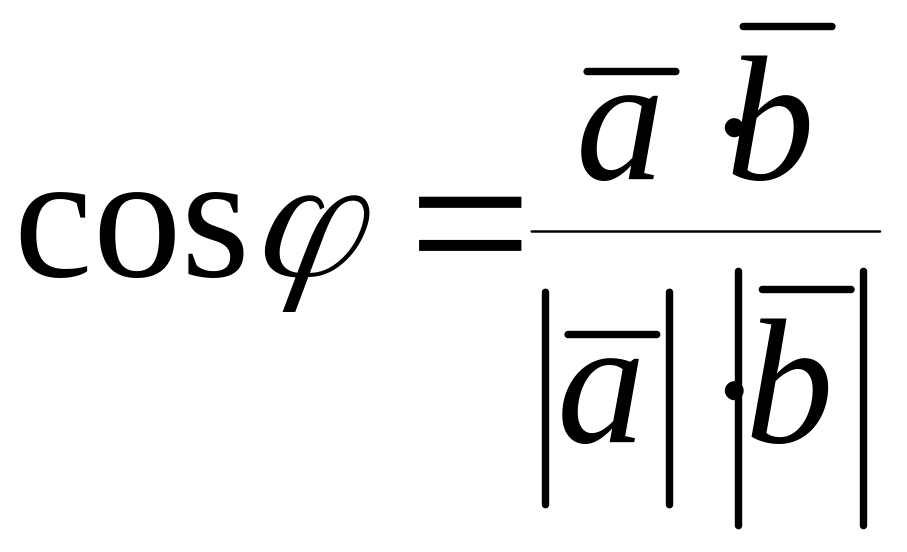или в координатной форме .

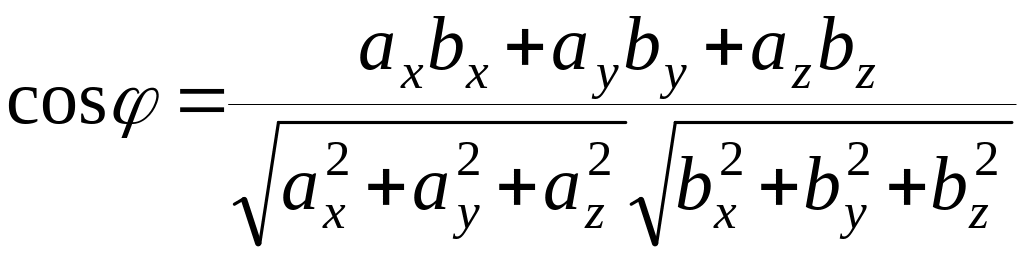Проекция вектора на ось вектора находится из соотношения:

,

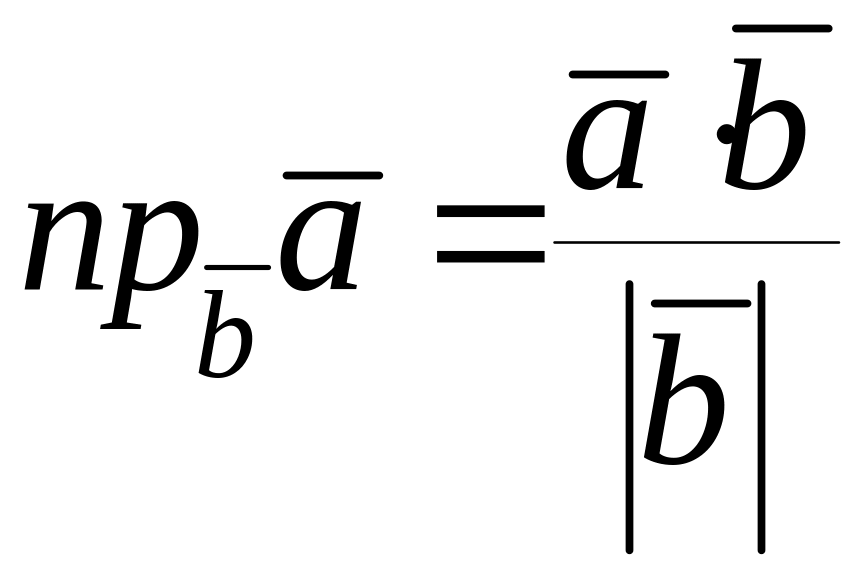или в координатной форме .

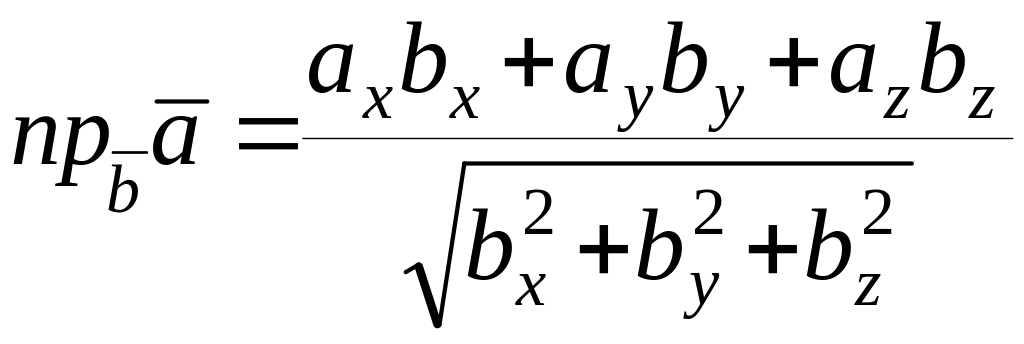Если учесть, что 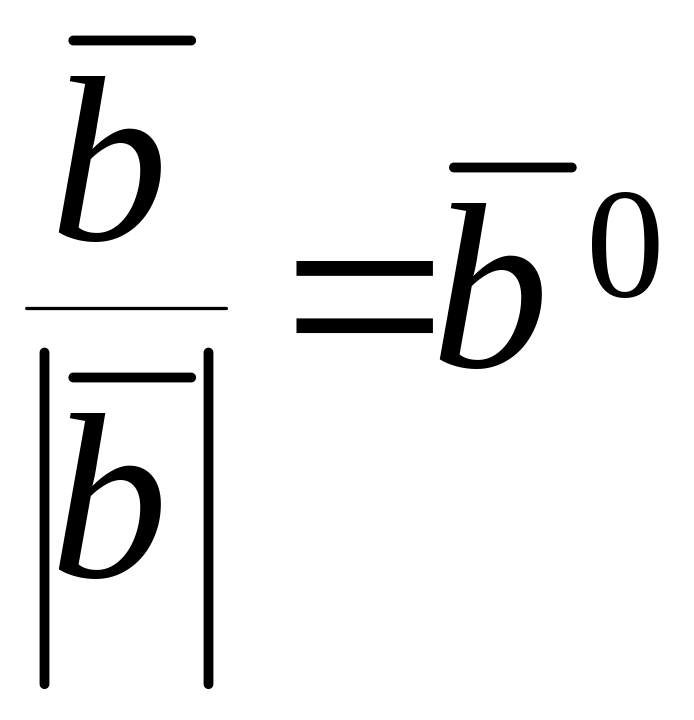- орт вектора, то .

Условием перпендикулярности ненулевых векторов и является равенство нулю их скалярного произведения:

.

Векторное произведение ненулевых векторов выражается через координаты данных векторов и следующим образом:

.

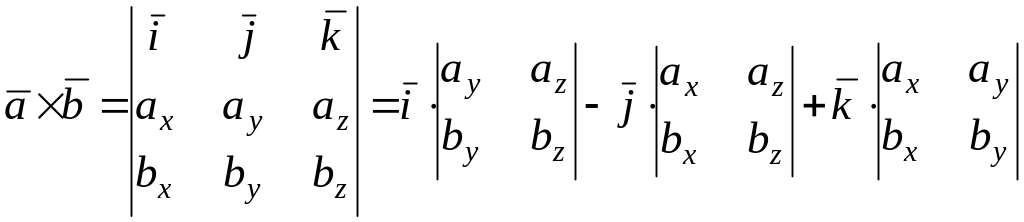Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е.  .

Скаляр , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:

.

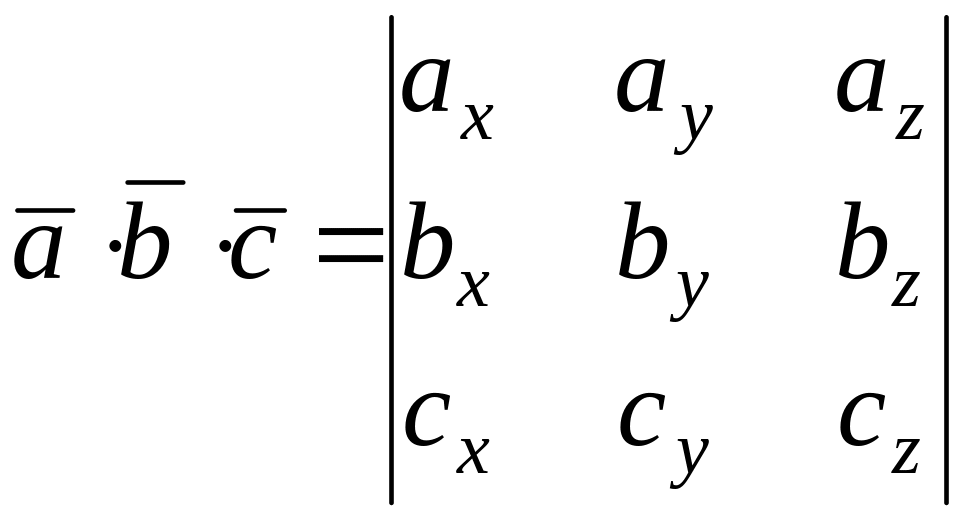Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности: .

Переход к новому базису

Координаты вектора зависят от выбора базиса. Выбор базиса ничем не ограничен, и принципиальное значение имеет задача о нахождении координат вектора в одном базисе по его координатам в другом базисе. Выясним, как устанавливается связь между координатами одного и того же вектора в различных базисах.

Пусть в пространстве имеются два базиса: старый и новый . Каждый из векторов (i =1,2,3) нового базиса можно выразить в виде линейной комбинации векторов старого базиса:

.

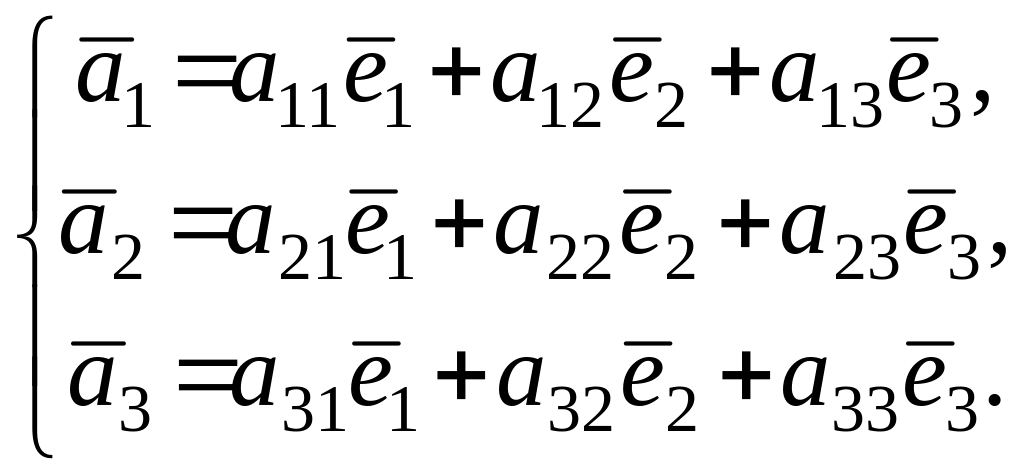Матрица (i,k=1,2,3) называется матрицей перехода от старого базиса к новому. Базисные векторы (i =1,2,3) линейно независимы, поэтому матрица неособенная.

Обратный переход от нового базиса к старому базису осуществляется с помощью обратной матрицы .

Найдем зависимость между координатами некоторого вектора в разных базисах. Пусть этот вектор имеет координаты относительно старого базиса и координаты относительно нового базиса, т.е. и

Подставив значения из предыдущей системы в первое равенство

для вектора и учитывая второе равенство, получим систему уравнений:

Как нетрудно заметить, матрицей перехода от новых к старым координатам будет транспонированная матрица . В матричном виде взаимосвязь между старыми координатами и новыми выражается следующими равенствами:

и .

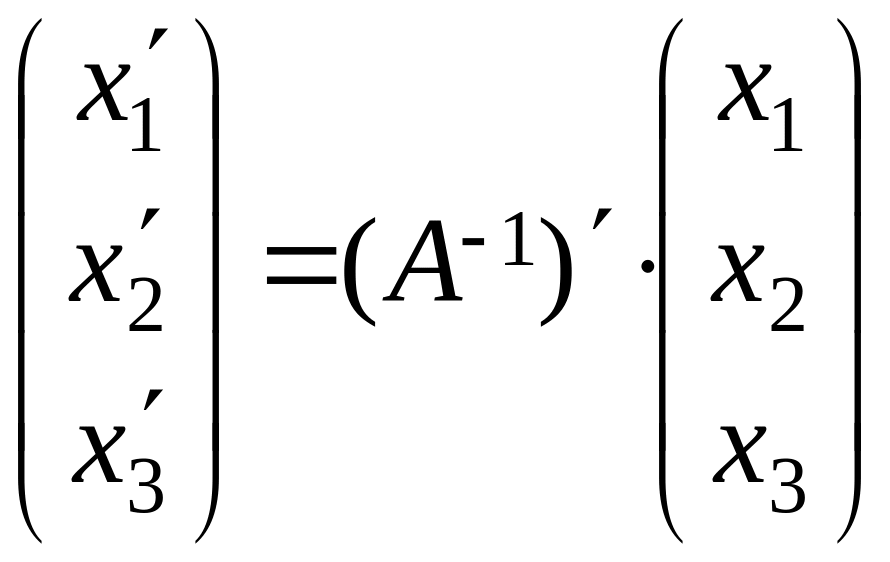Пример. В базисе заданы векторы и вектор . Показать, что векторы (i =1,2,3) образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.

Решение. Векторы образуют базис, если они линейно независимы. Составим векторное равенство или

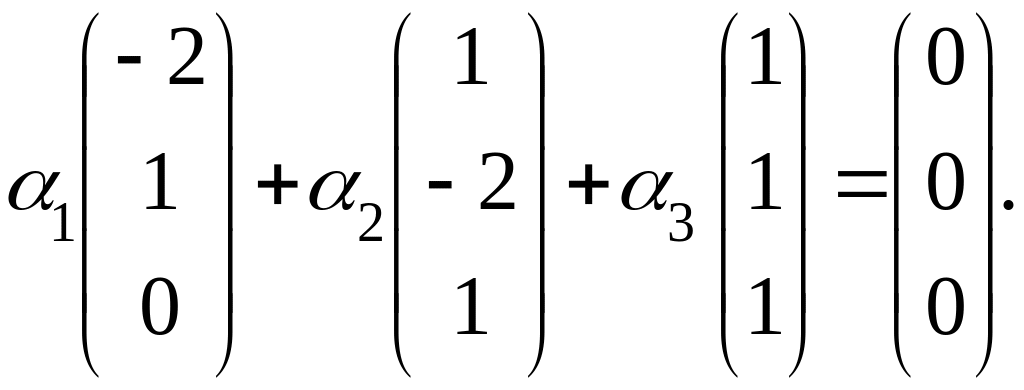
Задача сводится к решению системы:

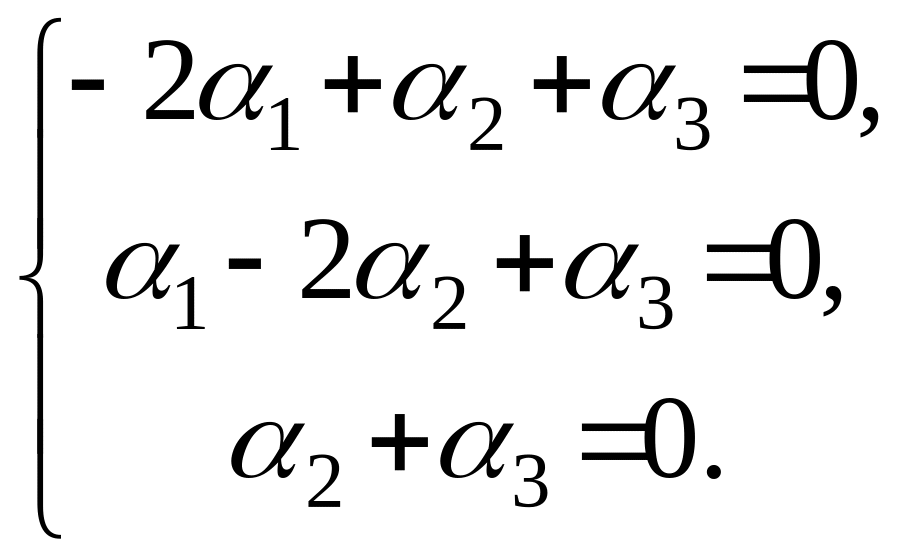
Определитель системы не равен нулю. Следовательно, однородная система имеет только нулевое решение , значит векторы линейно независимы и образуют базис.

Связь между старым базисом и новым выражается системой уравнений:

Матрица перехода от старого базиса к новому имеет вид

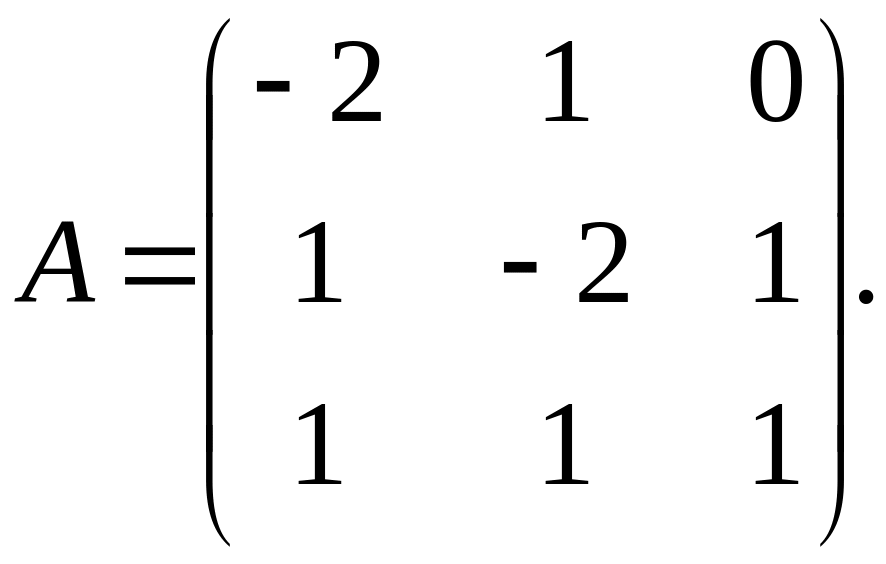
Вычисляем . Она имеет вид

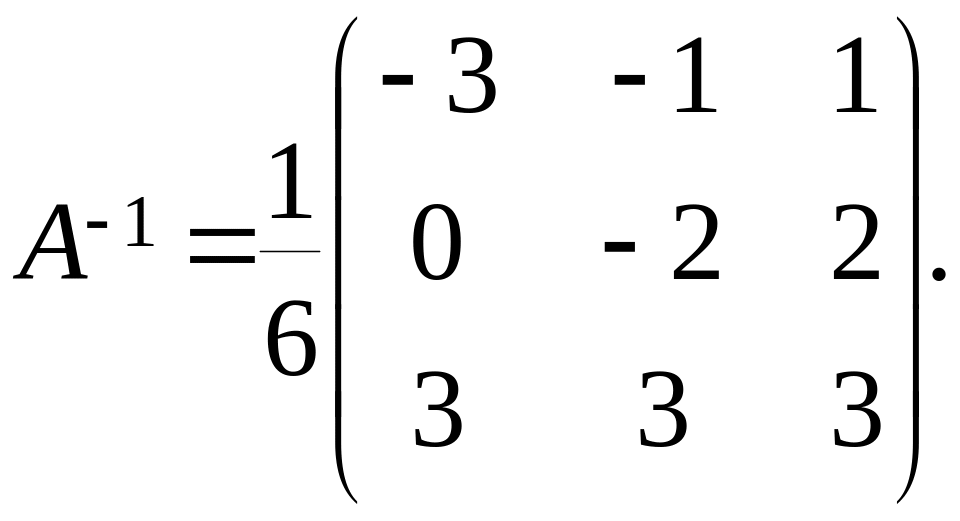
Находим транспонированную матрицу

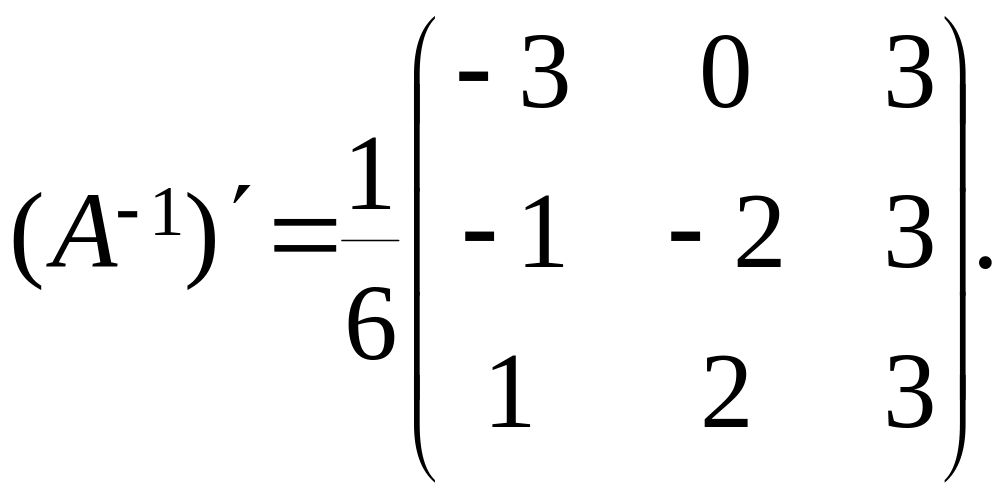
Координаты в новом базисе находим из равенства

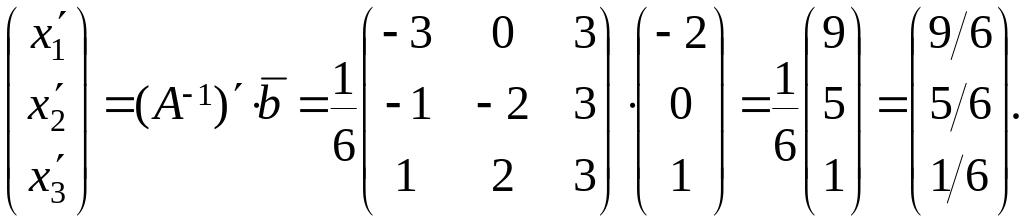
Новые координаты вектора в базисе есть (9/6, 5/6, 1/6) и вектор может быть представлен в виде: