
- •«Национальный исследовательский ядерный университет «мифи»
- •«Элементы векторной алгебры и аналитической геометрии»
- •Умножение векторов
- •Переход к новому базису
- •Решение типовых задач
- •Решение. Объём пирамиды найдем, исходя из геометрического свойства
- •Элементы аналитической геометрии
- •Плоскость и прямая в пространстве Рассмотрим геометрические объекты, которые описываются линейными алгебраическими уравнениями.
- •Решение типовых задач
- •Прямая на плоскости
- •Взаимное расположение двух прямых на плоскости
- •Решение типовых задач
- •Решение типовых задач
Решение типовых задач
Пример.
В некотором базисе
заданы три вектора
![]() ,
а также вектор
,
а также вектор
![]() .
Показать, что векторы
(i =1,2,3) образуют
базис и найти координаты вектора
в этом базисе.
.
Показать, что векторы
(i =1,2,3) образуют
базис и найти координаты вектора
в этом базисе.
Решение. Покажем, что векторы (i =1,2,3) – линейно независимы. Пусть линейная комбинация этих векторов обращается в нуль, т.е.
Это же равенство удобно записать в матричной форме:
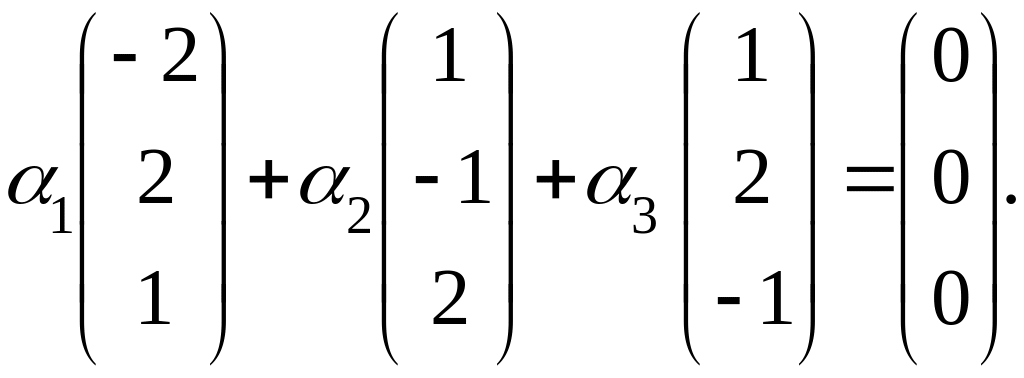
Задача сводится
к решению системы:
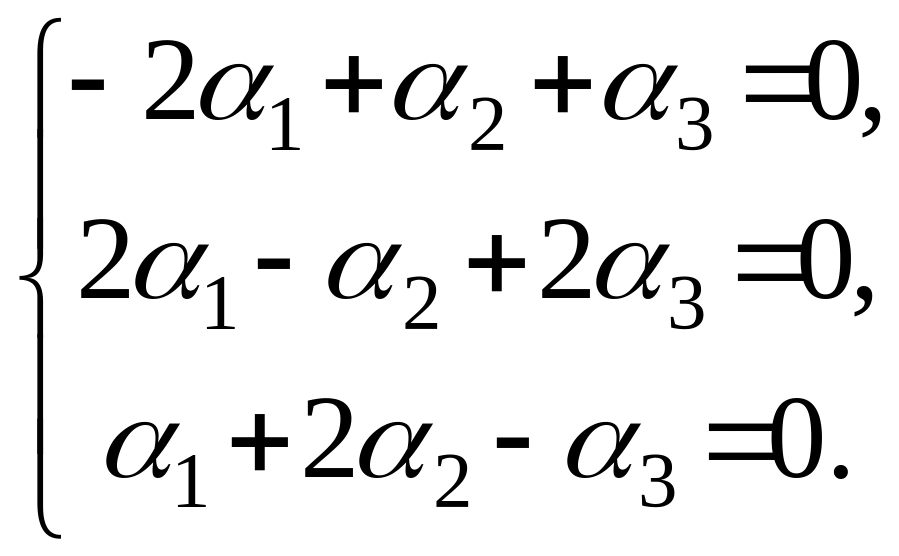
Убеждаемся
в том, что определитель системы не равен
нулю. Поэтому однородная система имеет
только нулевое решение. Следовательно,
,
а векторы
– линейно независимы и в трехмерном
пространстве образуют базис. Пусть
![]() – координаты вектора
в этом базисе. Это означает, что вектор
представим в виде
– координаты вектора
в этом базисе. Это означает, что вектор
представим в виде
![]() .
.
Запишем это равенство в координатной форме:
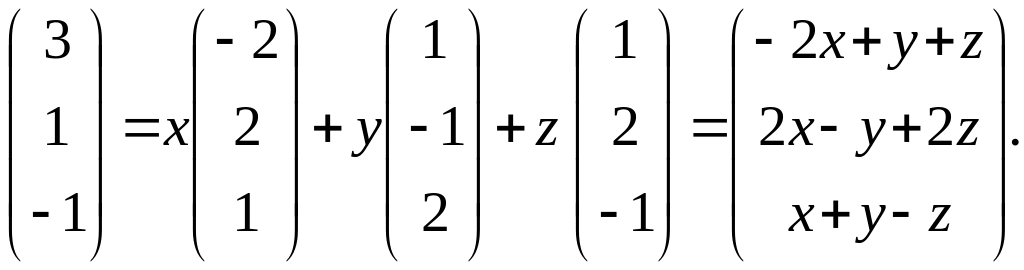
От этого равенства переходим к решению системы уравнений:
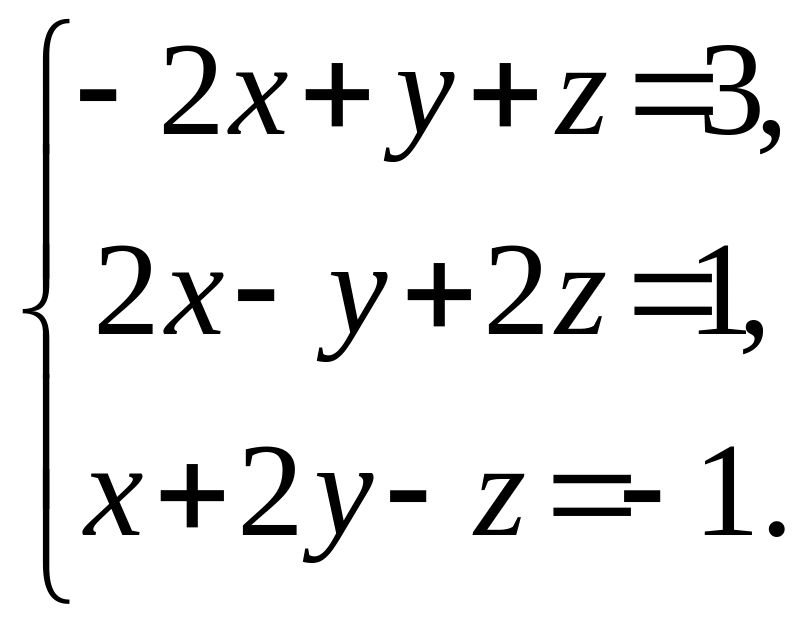
Решением этой
системы является тройка чисел
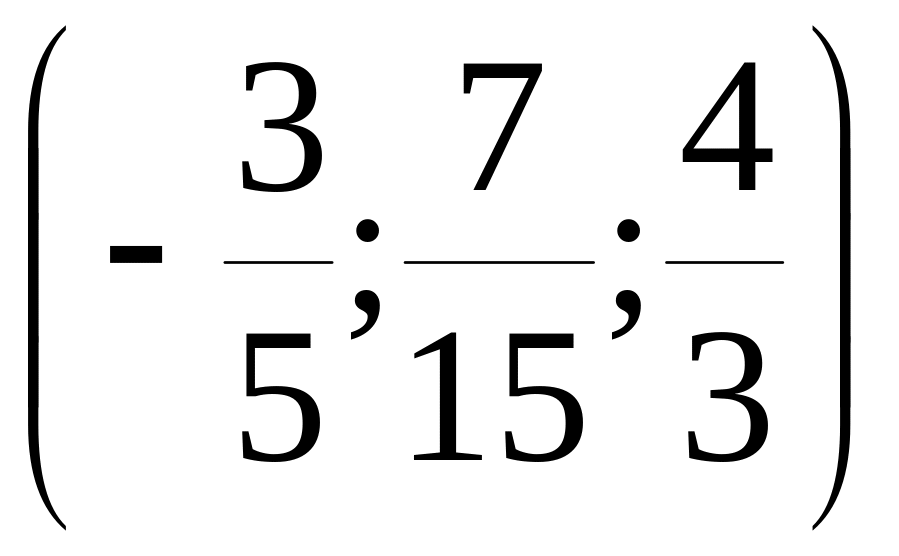 .
Они также являются координатами вектора
в новом базисе
.
Вектор
может быть представлен в виде:
.
Они также являются координатами вектора
в новом базисе
.
Вектор
может быть представлен в виде:
![]() или
или
![]() .
.
Пример:
Даны четыре точки
![]()
![]()
![]() .
.
Вычислить значение выражения
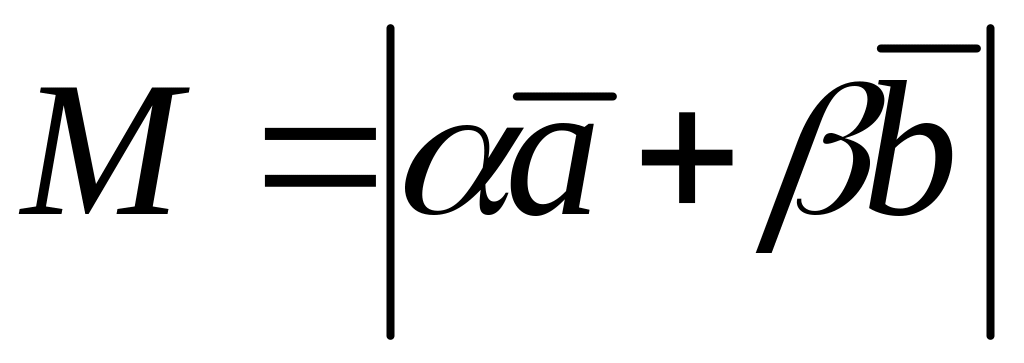 ,
где
,
где
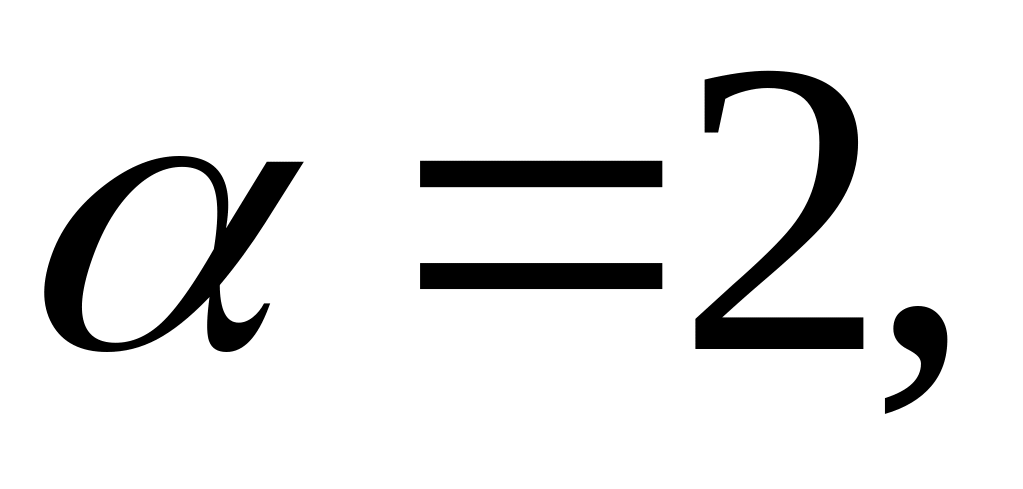
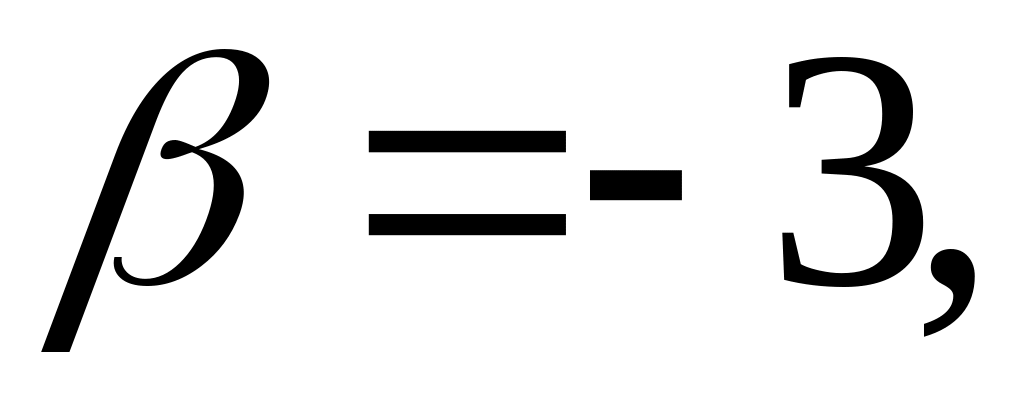
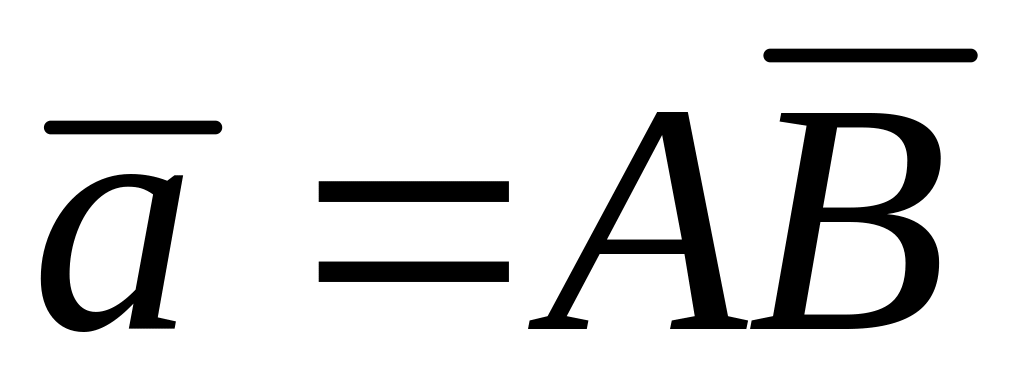 ,
,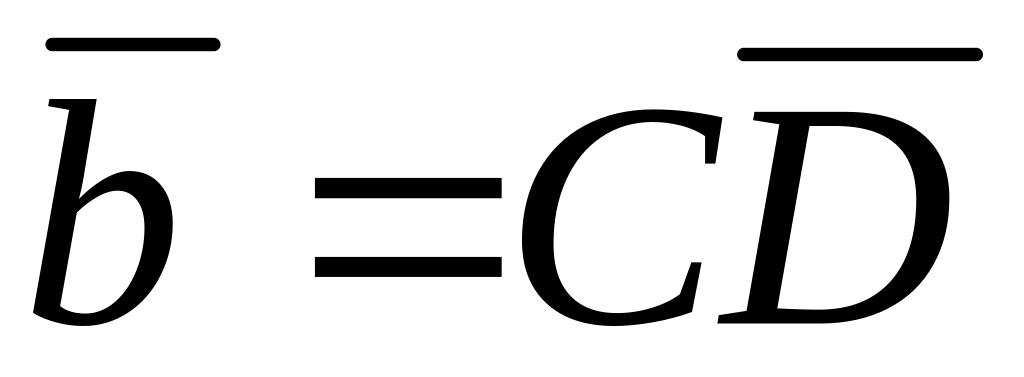 .
.
Решение.
Находим координаты векторов
и
через координаты начальной и конечной
точек:
![]() .
.
Найдем их линейную комбинацию:
![]() .
.
Вычислим модуль полученного вектора:
![]() .
.
2)
Найти
![]() и
и
![]() ,
где
,
где
![]() ,
,
![]() .
.
Решение.
Найдем координаты векторов
![]() и
:
и
:
![]() ,
,
![]() .
.
Найдем модули полученных векторов и их скалярное произведение:
![]() ,
,
![]() ,
,
![]() .
.
Определяем косинус угла между векторами:
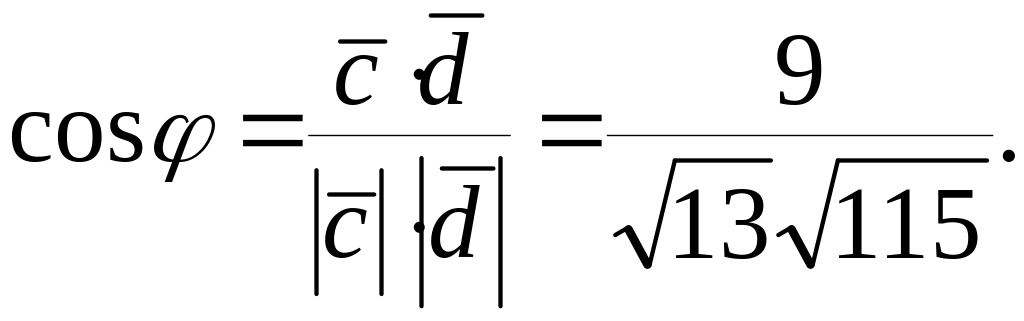
Найдем
проекцию вектора
на вектор
![]() :
:
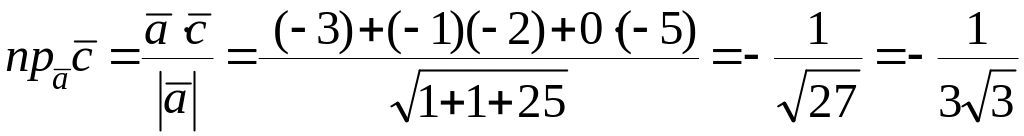 .
.
Определить длину медианы
 и стороны
и стороны
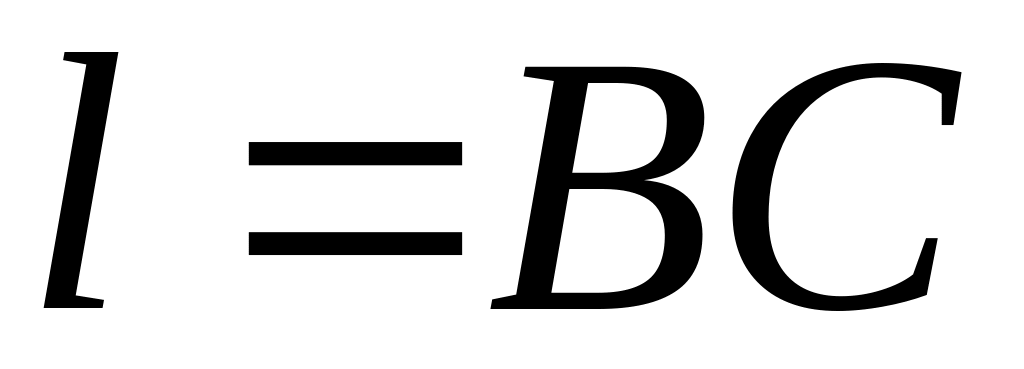 в треугольнике
в треугольнике
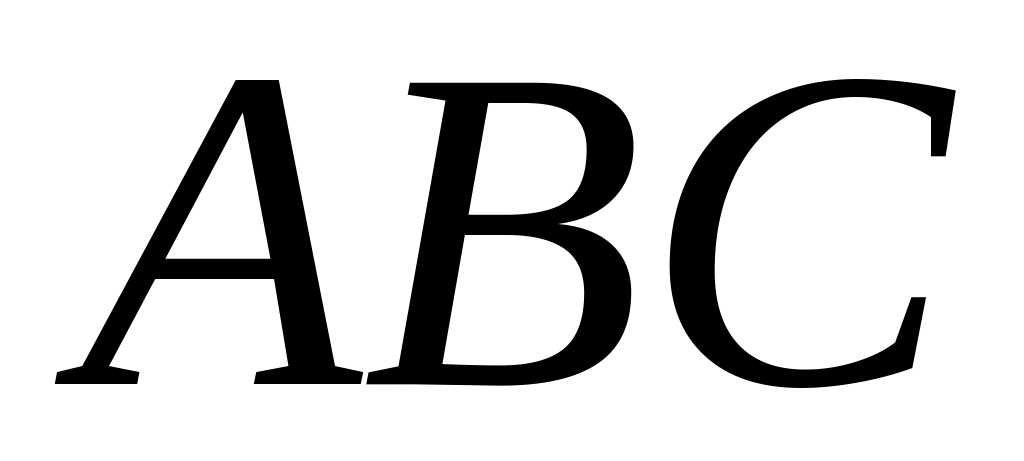 .
.
Решение.
Определим координаты точки![]() как
средней точки между
как
средней точки между![]() и
и
![]() :
: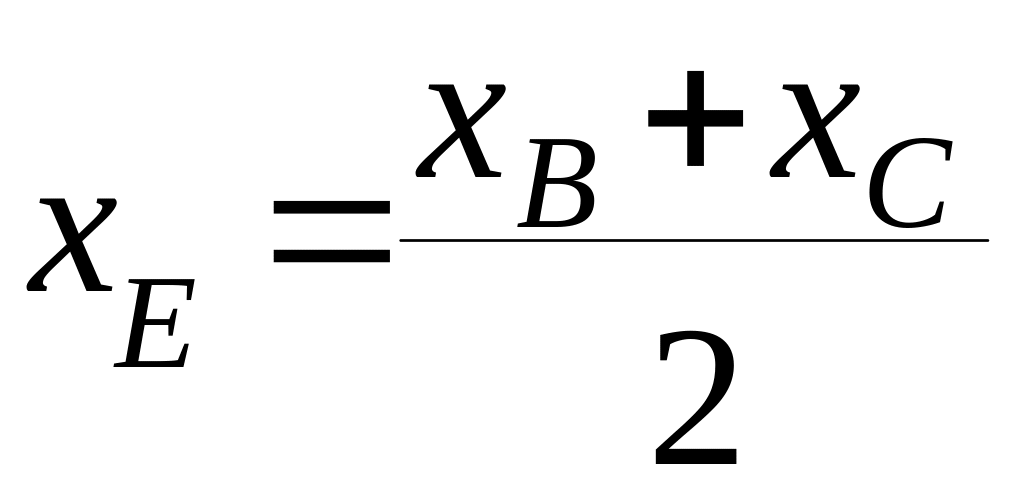 ;
;
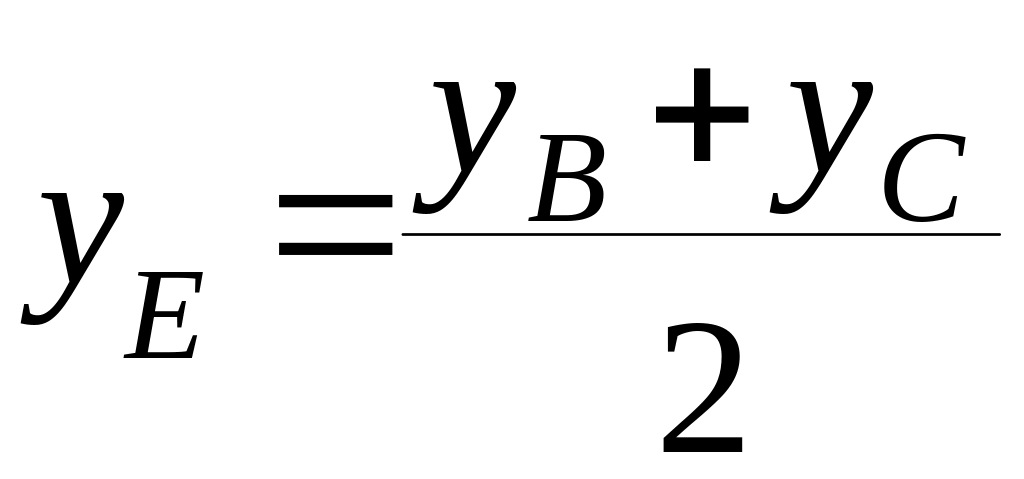 ;
;
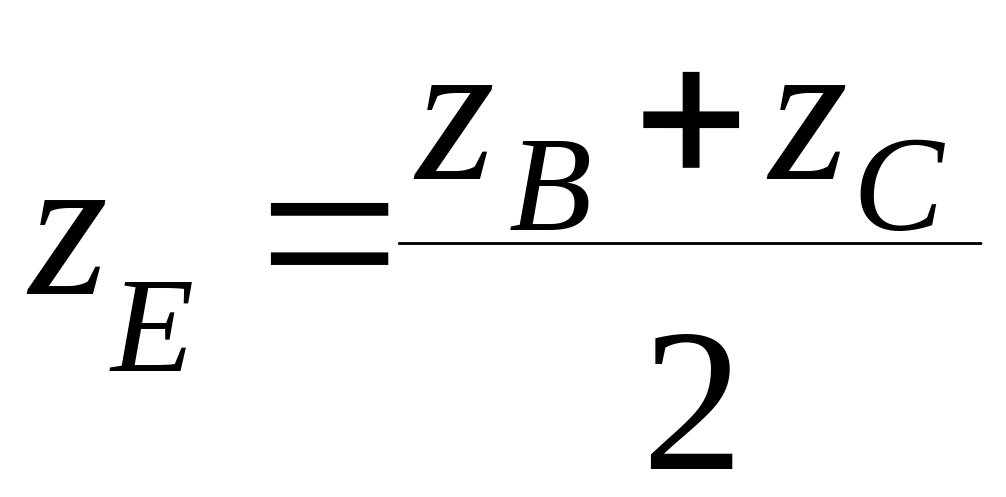 ;
;
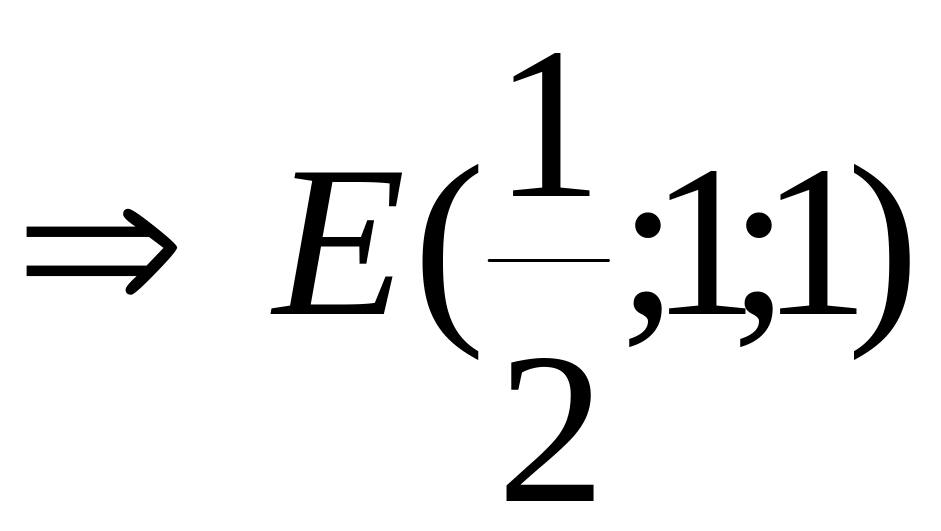 .
.
Вычислим
длину медианы
![]() и стороны
и стороны
![]() :
:
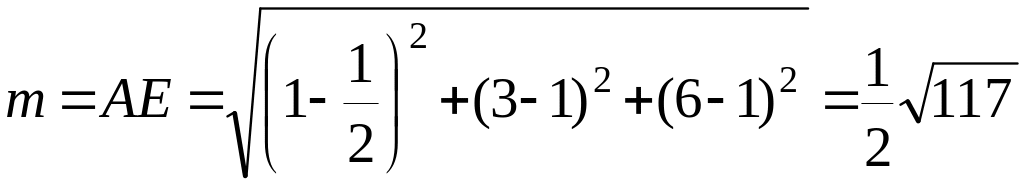 ;
;
![]() .
.
Вычислить площадь
 и его высоту
и его высоту
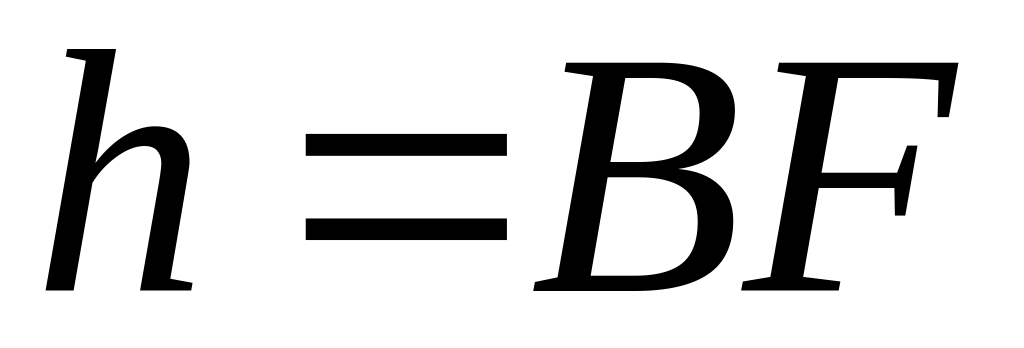 .
.
Решение.
Площадь треугольника найдем, исходя из
геометрического свойства векторного
произведения:
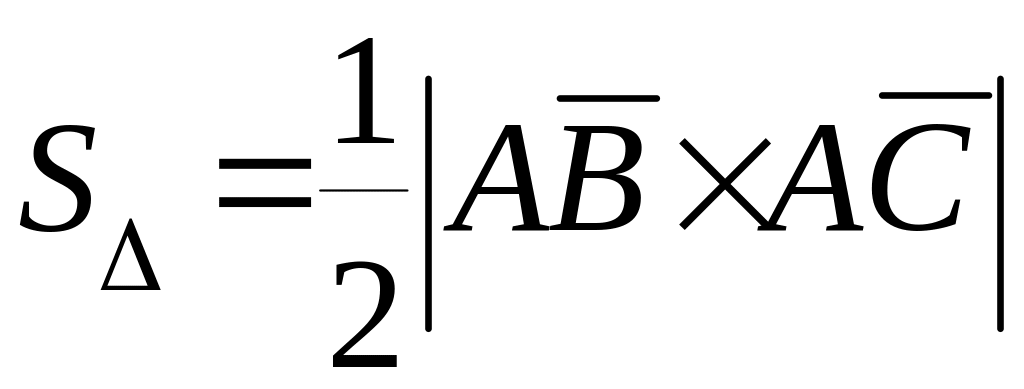 .
.
Найдем векторное произведение:
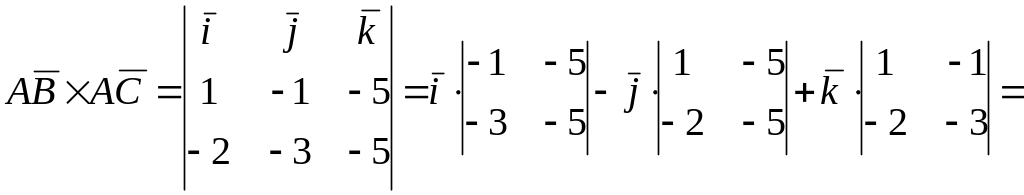
=![]() .
.
Тогда
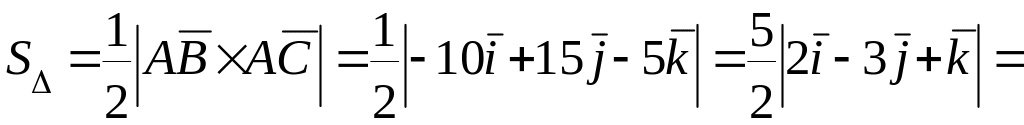
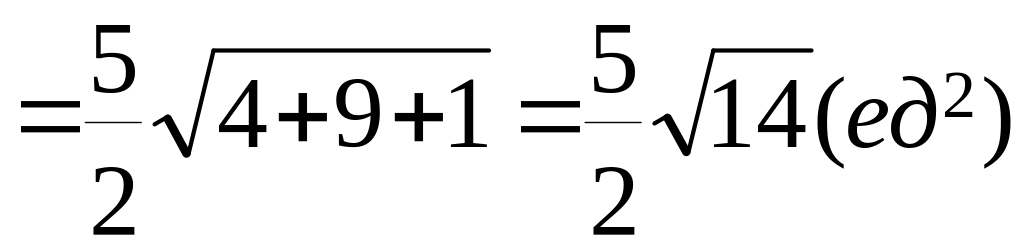 .
.
Определим
высоту
![]() ,
исходя из формулы
,
исходя из формулы
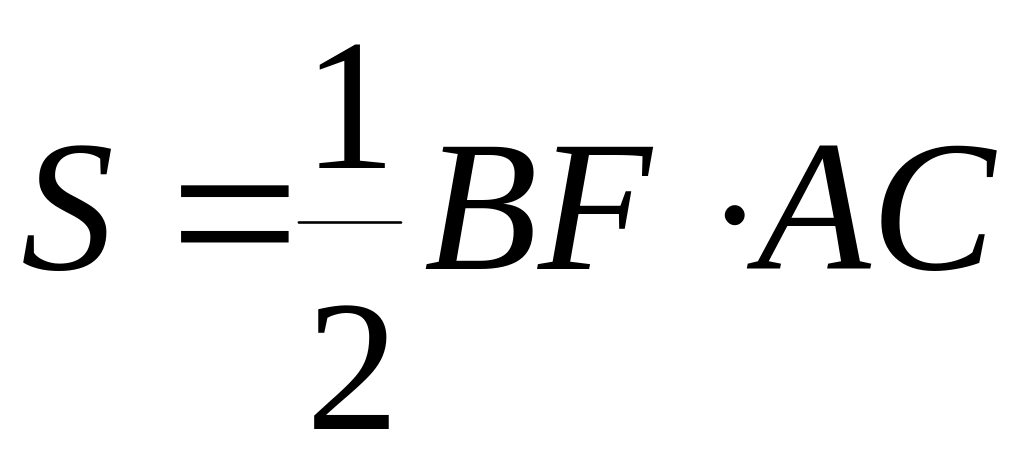 ,
откуда
,
откуда
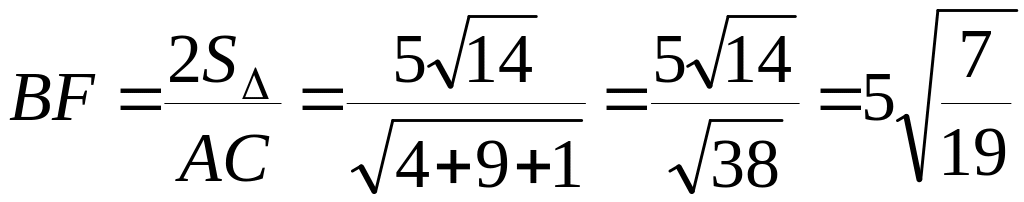 .
.
Найти объём пирамиды
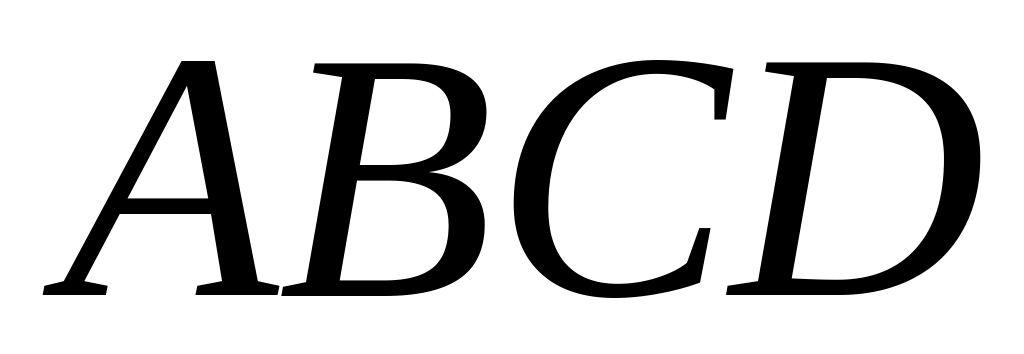 .
.
Решение. Объём пирамиды найдем, исходя из геометрического свойства
смешанного произведения:
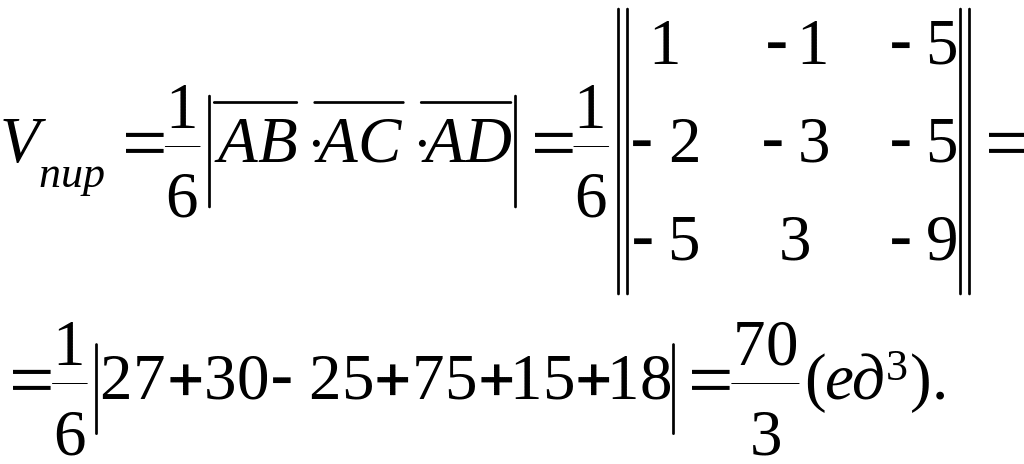 Высоту
пирамиды
Высоту
пирамиды
![]() найдем из формулы
найдем из формулы
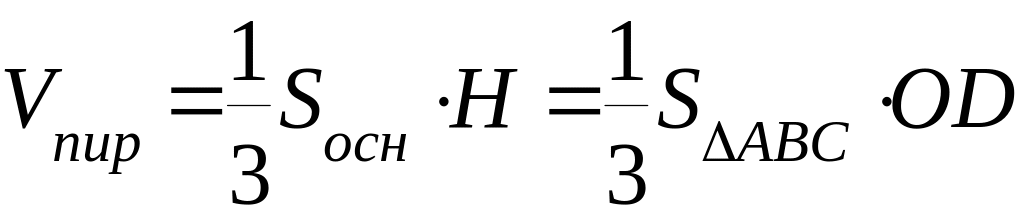 ,
,
откуда
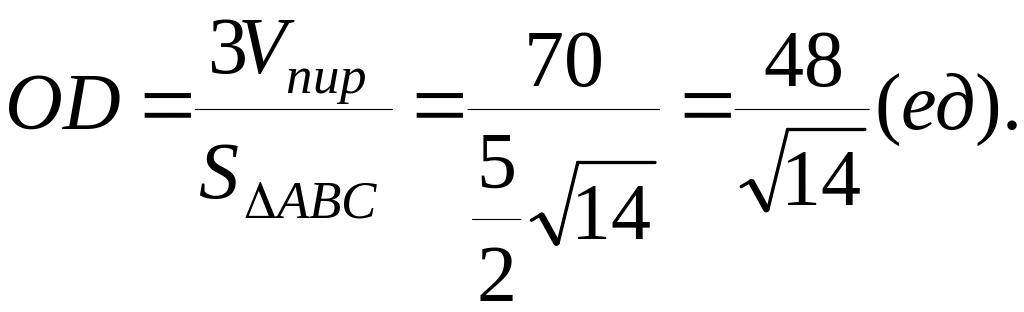
Элементы аналитической геометрии
Аналитическая геометрия на основе метода координат изучает геометрические объекты средствами алгебры. При этом геометрическим объектам сопоставляются уравнения (системы уравнений) так, что геометрические отношения (свойства) фигур выражаются в свойствах их уравнений.
Уравнение
![]() называется уравнением поверхности
(линии) в заданной системе координат,
если этому уравнению удовлетворяют
координаты
любой точки, лежащей на этой поверхности
(линии), и не удовлетворяют координаты
никакой другой точки, не лежащей на этой
поверхности (линии).
называется уравнением поверхности
(линии) в заданной системе координат,
если этому уравнению удовлетворяют
координаты
любой точки, лежащей на этой поверхности
(линии), и не удовлетворяют координаты
никакой другой точки, не лежащей на этой
поверхности (линии).
Понятие
уравнения геометрического объекта дает
возможность решать геометрические
задачи алгебраическими методами, не
прибегая к геометрическим построениям.
Например, задача нахождения точек
пересечения двух линий, определяемых
уравнениями
![]() и
и
![]() ,
сводится к алгебраической задаче решения
системы этих уравнений.
,
сводится к алгебраической задаче решения
системы этих уравнений.
