Министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Национальный исследовательский ядерный университет «мифи»

Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ

Методические указания

к выполнению индивидуальных заданий

по теме:

«Элементы векторной алгебры и аналитической геометрии»

Волгодонск

2010

Элементы векторной алгебры

Векторы и линейные операции над ними

В геометрии вектором называют направленный отрезок с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Таким образом, считается, что два направленных отрезка и , имеющие равные длины и одно и то же направление, определяют (изображают) один и тот же вектор , и пишут .

Длиной (или модулем) вектора называется число, равное длине отрезка АВ, изображающего вектор.

Векторы, параллельные одной прямой, называются коллинеарными и компланарными, если они параллельны одной плоскости.

Если вектор изображается направленным отрезком , то вектор, изображаемый направленным отрезком , называется вектором, противоположным вектору и обозначается - .

Для векторов вводятся операции сложения и вычитания. При этом заметим, что знаки «+» и «», которые ставятся между векторами, имеют другой смысл, чем в алгебре: они обозначают не алгебраическое, а геометрическое сложение векторов по правилу треугольника или параллелограмма.

Произведением вектора на число называется вектор , имеющий длину , направление которого совпадает с направлением вектора , если , и противоположно ему, если .

Сложение векторов и умножение их на число называются линейными операциями над векторами. Эти операции обладают свойствами по форме аналогичными свойствам сложения и умножения чисел.

Осью называется прямая l, положительное направление которой задается единичным вектором . Пусть - произвольный вектор, а А₁, В₁ ортогональные проекции точек А и В на ось l.

B

A

A₁ l⁰ B₁ l

Рис.1

Проекцией (или компонентой) вектора на ось l называется направленный отрезок на оси, началом которого служит проекция начала вектора , а концом - проекция конца этого вектора (рис.1). Очевидно, что компонента и вектор коллинеарны. Значит существует число (обозначим его ), такое, что . Число называется величиной проекции или координатой вектора на ось l и обозначается или . Координата численно равна модулю компоненты , взятой со знаком «+», если и со знаком «», если . Справедливо равенство . Часто именно это число называют проекцией вектора на ось l.

Пусть - векторы, а - действительные числа.

Вектор называется линейной комбинацией векторов .

Например, вектор является линейной комбинацией векторов .

Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам. В нашем примере вектор разложен по векторам .

Система n векторов называется линейно независимой, если из этих векторов невозможно составить нулевую линейную комбинацию, в которой хотя бы один из коэффициентов был бы отличен от нуля. Иными словами, векторы называются линейно независимыми, если равенство возможно лишь тогда, когда все . В противном случае система векторов линейно зависимая.

Для линейной зависимости двух векторов необходима и достаточна их коллинеарность, для трех векторов – их компланарность.

Если мы имеем два неколлинеарных вектора и , то всякий третий компланарный им вектор может быть единственным способом разложен по векторам и , т.е. представлен как сумма двух векторов, соответственно им компланарных: .

Если мы имеем три некомпланарных вектора , и , то всякий четвертый вектор может быть однозначно разложен по векторам , и , т.е. представлен как сумма трех векторов соответственно им коллинеарных: . Между четырьмя векторами существует линейная зависимость: , где не равны нулю одновременно.

Система n линейно независимых векторов в n -мерном пространстве называется базисом этого пространства.

На плоскости два неколлинеарных вектора , а в пространстве тройка некомпланарных векторов , взятых в определенном порядке, образуют базис.

Базис называется ортонормированным, если векторы взаимно перпендикулярные и единичные. Этот базис часто используется на практике и имеет специальное обозначение .

Говорят, что в пространстве задана прямоугольная (декартовая) система координат, если в этом пространстве указан ортонормированный базис и фиксированная точка О (начало координат), являющаяся общим началом базисных векторов. Векторы определяют положительное направление трех координатных осей: Оx (оси абсцисс), Oy (оси ординат) и Oz (оси аппликат), соответственно.

В пространственной прямоугольной системе координат вектор может быть представлен следующим образом: , где - координаты вектора относительно базиса , которые совпадают с проекциями вектора на соответствующие оси. Это векторное равенство часто записывают в символической форме: .

Если в прямоугольной системе координат точки А и В имеют координаты и , то координаты вектора находятся как разности

соответствующих координат конца В и начала А этого вектора, т.е.

,

а модуль его определяется как расстояние между двумя точками:

.

Если учесть при этом, что , то выражение для модуля вектора можно записать так: .

Пусть углы вектора с осями Ox, Oy, Oz соответственно равны .

Направляющие косинусы вектора определяются по формулам: ; ; .

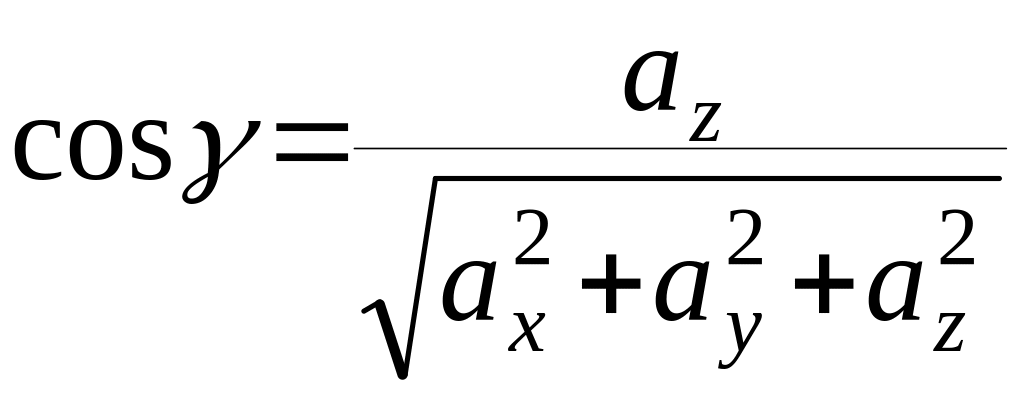Эти числа являются координатами орта , т.е. , и связаны равенством .

Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.

Линейные операции над векторами, заданными своими координатами и , выполняются по следующим правилам:

1) при сложении двух векторов их одноименные координаты складываются: ;

2) при умножении вектора на число все его координаты умножаются на это число: .

Два вектора равны, если равны их соответствующие координаты, т.е. .

Два вектора коллинеарные, если их координаты пропорциональны.

Итак, если  , то или .