1.7.2. Многоканальные смо с приоритетами

Класс СМО .

Потоки заявок всех приоритетов – пуассоновские, время обслуживания распределено по экспоненциальному закону. Интенсивность обслуживания произвольной заявки определяется по формуле:

.

Введем обозначения: .

Как и в одноканальной СМО с приоритетами, в данной СМО время ожидания в очереди заявки k-го приоритета равно (см. формулу (1.51)):

.

Проделав выкладки, как и для одноканальной СМО, получим:

, (1.63)

где .

Чтобы определить , рассмотрим СМО без приоритетов:

. (1.64)

Среднее время ожидания заявок в очереди для СМО без приоритетов определяется по формуле (см. п. 4.1.2):

, (1.65)

где .

Приравнивая (1.64) и (1.65), получим: .

В результате получаем: .

Если использовать замену , то получим:

,

а вычислим по формуле (1.63).

Далее, используя формулы Литтла, определим:

,  ,  .

1.8. Оптимизация параметров смо

При проектировании или совершенствовании СМО возникает задача оптимизации ее параметров. От качества обслуживания зависят затраты на СМО и потери в СМО.

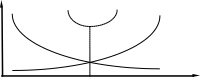
потери от низкого затраты на

уровня функционирование

обслуживания СМО

оптимальный уровень качество

качества обслуживания

Рис. 1.31. Определение оптимального уровня качества СМО

Ставится задача определения оптимального уровня качества обслуживания. Можно сформулировать большое число задач оптимизации СМО, формируя различные целевые функции. В данном разделе в качестве примеров рассмотрено несколько постановок таких задач.

Задача оптимальной интенсивности обслуживания в одноканальной смо с бесконечной очередью

Класс СМО .

– целевая функция, где – потери в единицу времени от пребывания заявки в СМО, – затраты в единицу времени при увеличении интенсивности обслуживания на единицу.

С учетом того, что , получим целевую функцию: . Для определения минимума целевой функции найдем производную:

.

Искомая оптимальная интенсивность находится из уравнения:

,

.

Задача оптимальной интенсивности в одноканальной смо без очереди

– целевая функция, где – потери от отказа в обслуживании (доходы от обслуживания одной заявки), – затраты в единицу времени при увеличении интенсивности обслуживания на единицу (то же, что в предыдущей задаче).

Поскольку , , то

,

,

откуда получим:

.

Задачи оптимизации параметров многоканальной смо

Класс СМО .

Определение оптимального числа каналов. Сформируем целевую функцию: , где – затраты в единицу времени на функционирование одного канала, – то же, что в задачах оптимальной интенсивности, рассмотренных выше. В данном классе СМО не удается аналитически определить оптимальное число каналов. Поэтому необходимо построить зависимость используя аппарат анализа многоканальных СМО (см. п. 1.4.2) и по определить оптимальное число каналов.

Класс СМО .

Определение оптимального числа мест в очереди

Для данного класса СМО целевая функция имеет вид:

, где – затраты в единицу времени на поддержание одного места в очереди, , – те же коэффициенты, что в задачах оптимальной интенсивности в одноканальной СМО. В этой задаче тоже не удается аналитически определить оптимальное число каналов. Поэтому необходимо построить зависимость и определить оптимальное число мест в очереди.