1.6.2. Анализ непуассоновских смо методом вложенных цепей Маркова

Анализ СМО с произвольным временем обслуживания

Рассмотрим СМО класса .

Будем называть момент выхода из системы обслуженной заявки моментом регенерации системы.

Определим – вероятность поступления ровно заявок в СМО между моментами регенерации. Искомая вероятность вычисляется по формуле:

.

Обозначим состояния СМО: – в системе находится заявок.

Матрица переходов из одного состояния в другое имеет вид:

Отметим, что .

Строка матрицы совпадает со строкой , потому что рассматривается интервал между моментами регенерации (моментами выхода заявки из СМО). Эти интервалы не отличаются, была ли в СМО одна заявка в предыдущий момент регенерации (она находилась на обслуживании) или заявок в СМО вообще не было.

Составим систему уравнений для нахождения предельных вероятностей.

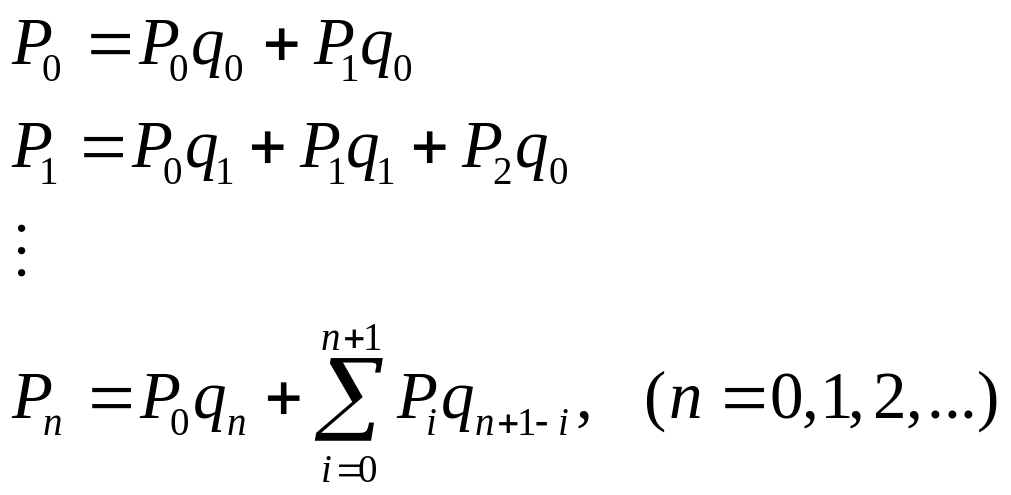
Используем Z–преобразование для определения характеристик СМО (основные положения Z–преобразования приведены в приложении 3):

;

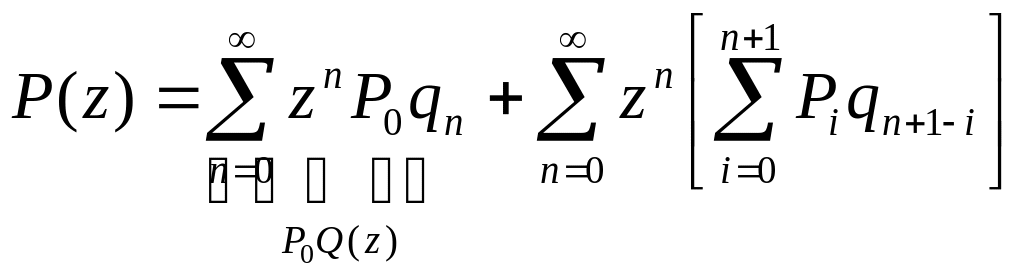. (1.43)

Преобразуем второе слагаемое:

.

Сделаем замену :

.

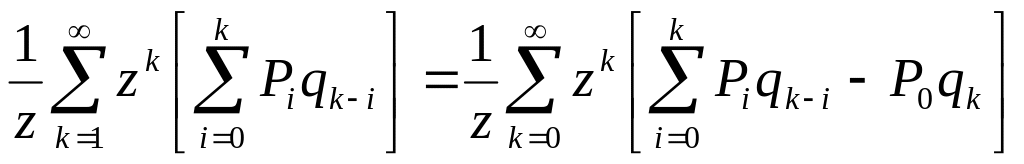. (1.44)

Выражение (1.44) можно также получить, используя свойство Z–преобразования:

.

Подставляя (1.44) в (1.43), получим:

.

Откуда

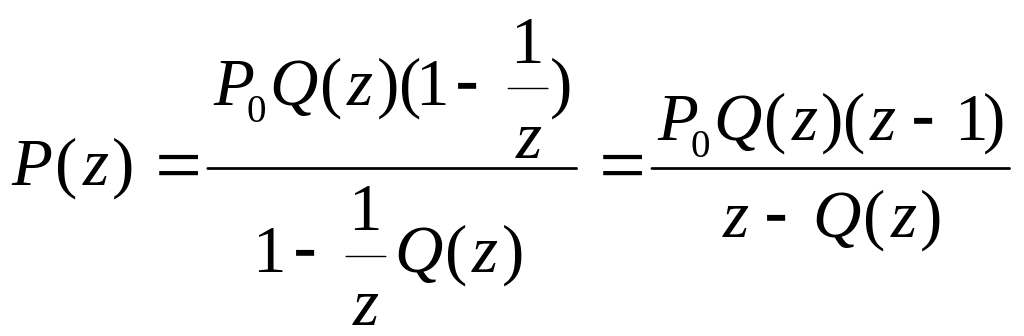. (1.45)

Рассмотрим подробнее :

;

;

;

;

; (1.46)

;

. (1.47)

Чтобы определить в (1.45), надо использовать свойство Z–преобразования:

.

При подстановке в (1.45) получим неопределенность. Применим правило Лапиталя для нахождения предела .

Берем производную числителя и знаменателя:

.

Учитывая (4) и тот факт, что , получим:

.

Откуда

. (1.48)

Для существования установившегося режима в СМО (чтобы очередь не росла до бесконечности) необходимо, чтобы .

Получим выражение для определения . Для этого возьмем производную от :

.

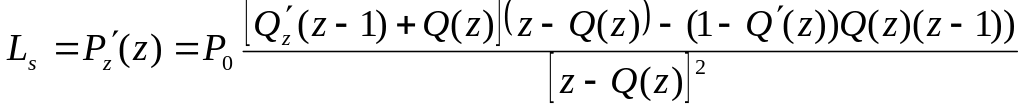После преобразования получим:

.

Среднее число заявок в СМО равно:

.

Чтобы разрешить неопределенность, воспользуемся правилом Лапиталя:

;

.

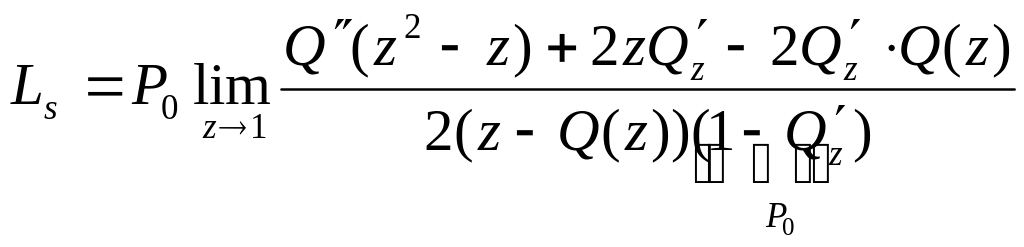Чтобы вновь снять неопределенность, еще раз воспользуемся правилом Лапиталя:

;

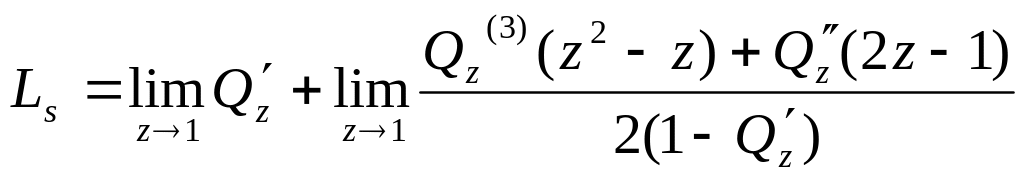. (1.49)

После подстановки в (1.49) выражения (1.46) и (1.47), получим:

, (1.50)

которая носит имя формулы Хинчина –Поллачека.

; ; ;

.

Примеры анализа СМО методом вложенных цепей Маркова

Пример 1. Пусть , тогда: и .

При подстановке математического ожидания и дисперсии в формулу Хинчина–Поллачека получаем ту же формулу , которая была получена в п. 1.4.1 для пуассоновских систем:

.

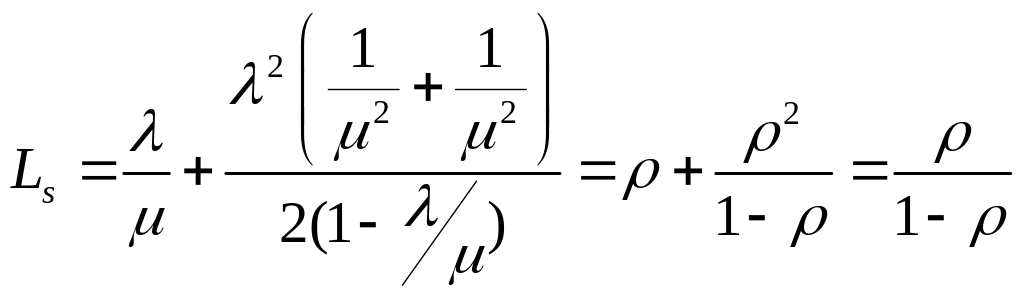Пример 2. Пусть – время обслуживания – постоянная величина, т.е. . После подстановки в формулу Хинчина–Поллачека получим выражение для :

.

СМО с произвольным входным потоком

Класс СМО .

В этом случае моменты регенерации системы – моменты поступления заявок в СМО.

Матрица переходов из одного состояния в другое имеет вид:

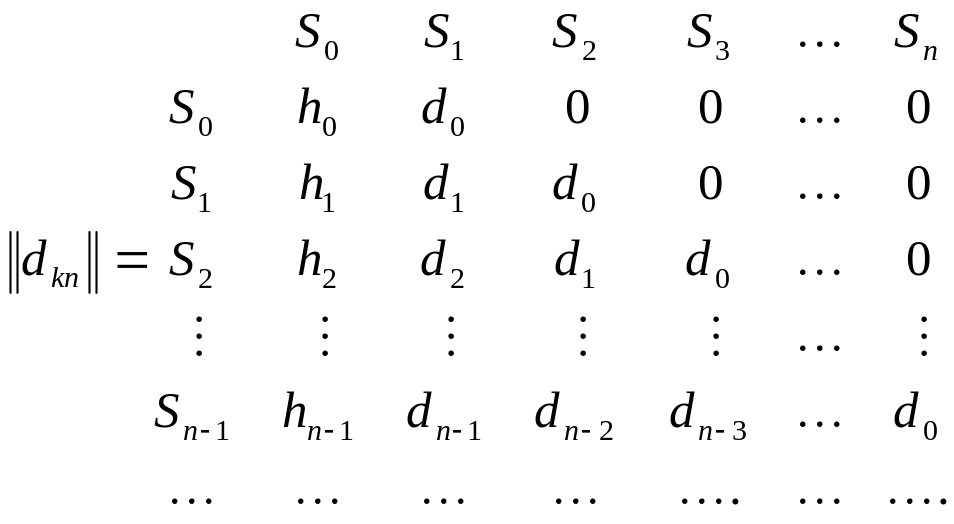
где – вероятность того, что между моментами регенерации СМО будет обслужено 0 заявок; – вероятность того, что между моментами регенерации СМО будет обслужено ровно заявок, которая определяется по формуле:

.

Вероятности вычисляются из условия, что сумма вероятностей по каждой строке равна единице:

.

Предельные вероятности найдем из уравнения :

Будем находить решение системы уравнений в виде:

, где , а – постоянный коэффициент.

( )

.

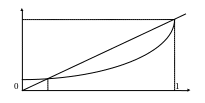
При это уравнение имеет единственное решение , покажем это (рис. 1.29). Введем обозначение :

; ;

.

Рис. 1.29. График функции

Так как и , то функция – выпуклая и монотонно – возрастающая. Чтобы было единственным решением, необходимо, чтобы .

;

;

.

Значит, существует, если .

Решая уравнение , находим . Для определения коэффициента В воспользуемся соотношением :

;

;

.

Таким образом, .

Определим характеристики СМО:

;

;

;

;

;

;

.

Примеры анализа СМО методом вложенных цепей Маркова

Пример 1.Пусть входной поток – пуассоновский, т.е. .

Составим уравнение для определения : ;

;

.

Решаем уравнение

.

Решением данного уравнения будет ; , т.е. получаем ту же формулу , которая была получена в п. 1.4.1 для пуассоновских систем.

Пример 2. Пусть входной поток в СМО – регулярный, т.е. интервал между поступлениями заявок .

Составляем уравнение для :

;

.

Находим из полученного уравнения.

; ; ; .