1.6. Непуассоновские смо

Для анализа непуассоновских СМО следует использовать имитационное моделирование. Вопросы имитационного моделирования рассматриваются во множестве пособий и учебников, см., например, [4,5]. Вместе с тем, для некоторых классов непуассоновских СМО можно произвести аналитические расчеты характеристик. Это СМО, в которых входной поток непуассоновский, или время обслуживания – не экспоненциальное распределение. В данном разделе будут рассмотрены именно такие СМО.

1.6.1. Анализ непуассоновских смо методом Эрланга

Суть этого метода заключается в аппроксимации непуассоновского потока потоком Эрланга – го порядка.

а) СМО с произвольным законом времени обслуживания

Класс СМО , где – произвольная функция распределения.

Определив по математическое ожидание и дисперсию времени обслуживания , аппроксимируем распределением Эрланга k–го порядка (см. раздел 1.2) . Вопросы анализа таких СМО рассмотрим последовательно по мере усложнения для Эрланга 2-го, 3-го и т.д. порядка.

Пусть время обслуживания распределено в соответствии с законом Эрланга 2-го порядка: (т.е. в пуассоновском потоке вычеркивается каждый второй элемент ).

Процесс обслуживания будем представлять как последовательность двух этапов, на каждом из которых обслуживание ведется по экспоненциальному закону с .

Размеченный граф такой СМО приведен на рис. 1.22.

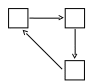
Рис. 1.22. Размеченный граф одноканальной СМО без очереди

и временем обслуживания Эрланга 2-го порядка

Состояния СМО: – в системе нет заявок; – в системе одна заявка и обслуживается на первом этапе; – в системе одна заявка и проходит второй этап обслуживания.

Найдем предельные вероятности:

; ;

; ;

; .

Р ассмотрим СМО, в которой – распределение Эрланга третьего порядка:

Рис. 1.23. Размеченный граф СМО с временем обслуживания

Эрланга третьего порядка

После решения системы уравнений получим предельные вероятности:

;

;

.

Получаем те же самые формулы, что и для СМО с – Эрланга второго порядка.

Следовательно, для одноканальных систем без очереди для закона Эрланга любого порядка получаем одни и те же формулы.

Рассмотрим СМО с ограниченной очередью: , где – распределение Эрланга второго порядка. Размеченный граф такой СМО приведен на рис. 1.24:

Рис. 1.24. Размеченный граф одноканальной СМО с ограниченной очередью и временем обслуживания Эрланга 2-го порядка

Состояния системы:

– число заявок в СМО – i, и заявка обслуживается на первом этапе;

– заявка проходит обслуживание на втором этапе.

Е сли – закон Эрланга третьего порядка, т.е. , то надо добавить еще один ярус в размеченный граф:

Рис. 1.25. Размеченный граф одноканальной СМО с ограниченной    очередью и временем обслуживания Эрланга третьего порядка

Не составляет трудностей построить размеченный граф и для многоканальных СМО для времени обслуживания распределенном по закону Эрланга k – порядка, чтобы получить предельные вероятности и затем характеристики СМО.

б) СМО с произвольным входным потоком

Класс СМО , где – произвольное распределение. Аппроксимируем распределением Эрланга k – го порядка.

Рассмотрим сначала СМО, в которой – распределение Эрланга второго порядка.

В данных СМО интервал времени между заявками представим в виде двух этапов, каждый из которых распределен по экспоненциальному закону с . Состояния системы будут иметь двойной индекс.

– в системе заявок, и формирование заявки проходит первый этап.

– формирование заявки проходит второй этап.

Размеченный граф такой СМО приведен на рис. 1.26 :

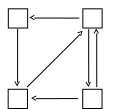
Рис. 1.26. Размеченный граф одноканальной СМО без очереди 

с входным потоком Эрланга второго порядка

Обозначим через , получим систему уравнений:

Составим уравнение для нахождения P₁₁:

.

Остальные вероятности равны;

.

Определим характеристики СМО:

;

;

;

Рассмотрим СМО, в которой входной поток – поток Эрланга третьего порядка .

Размеченный граф такой СМО приведен на рис. 1.27 :

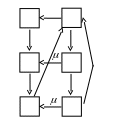
Рис. 1.27. Размеченный граф СМО с входным потоком Эрланга третьего порядка

Для определения характеристик такой СМО надо рассчитать предельные вероятности , а затем .

Рис. 1.28. Размеченный граф одноканальной СМО с ограниченной

очередью и входным потоком Эрланга второго порядка

Для СМО с ограниченной очередью строится граф увеличением числа состояний, как это делается для пуассоновских СМО. На рис. 1.28 приведен граф для одноканальной СМО с входным потоком Эрланга 2-го порядка и максимальной длиной очереди N=2.

Чтобы определить характеристики СМО, необходимо рассчитать предельные вероятности , а затем .

Нет принципиальных трудностей и для анализа СМО с входным потоком Эрланга – го порядка.