1.9. Смешанное произведение векторов

Смешанным произведением векторов , и называется число , равное скалярному произведению (  ). Из этого определения следует, что если векторы , и компланарны, то их смешанное произведение равно нулю. Действительно, если данные векторы компланарны, то вектор  перпендикулярен вектору , а значит, скалярное произведение этих двух векторов равно нулю. Обратно, если смешанное произведение равно нулю, то либо хотя бы один из векторов нулевой (и тогда , и компланарны); либо векторы и  перпендикулярны (и тогда вектор лежит в плоскости векторов и , то есть векторы опять-таки компланарны). Таким образом, мы получили первое свойство смешанного произведения:

= 0 тогда и только тогда, когда векторы , и компланарны.

Пусть теперь данные векторы не компланарны. Тогда  =  (  )=  ^.  ^.cos, где  – угол между векторами и  , то есть угол между вектором и перпендикуляром к плоскости векторов и . А тогда  ^. cos – это высота параллелепипеда, построенного на векторах , и . Если учесть, что    – это площадь параллелограмма, который является основанием указанного параллелепипеда, то получается, что

модуль смешанного произведения некомпланарных векторов равен объему параллелепипеда, построенного на этих векторах.

Далее, для некомпланарных множителей получаем, что смешанное произведение положительно, если указанный угол  – острый. Можно доказать, что это равносильно тому, что тройка векторов ( , , ) – правая. Аналогично, смешанное произведение отрицательно, если эта тройка – левая.

Итак, знак смешанного произведения некомпланарных векторов зависит от того, правую или левую тройку они образуют:

> 0 тогда и только тогда, когда тройка ( , , ) – правая;

< 0 тогда и только тогда, когда тройка ( , , ) –

левая.

Из сказанного следует равенство смешанных произведений:

= = .

Действительно, модули всех трех произведений равны объему одного и того же параллелепипеда, а тройки ( , , ), ( , , ) и ( , , ) – либо все правые, либо все левые.

С другой стороны, тройки ( , , ) и ( , , ) – разноименные, поэтому

= – .

Пусть теперь векторы заданы своими координатами: =(a_x;a_y;a_z), =(b_x;b_y;b_z), =(c_x;c_y;c_z). Тогда, используя формулы для скалярного и векторного произведения, получим: = a_x +a_y +a_z .

Для записи смешанного произведения можно использовать определитель третьего порядка. Так называется число, обозначаемое 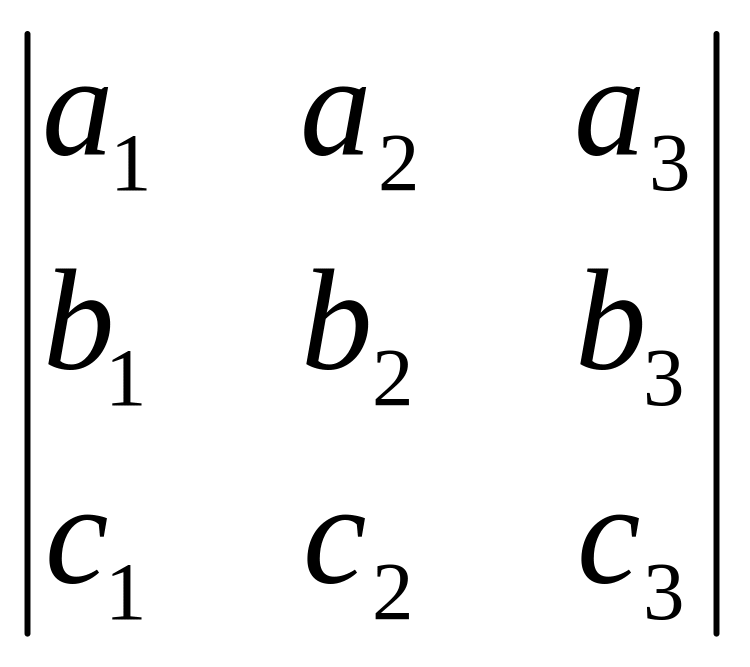и равное

a₁ –a₂ +a₃ . Заметим, что =

= b_zc_x–b_xc_z = – . Поэтому получаем формулу для вычисления смешанного произведения:

= .

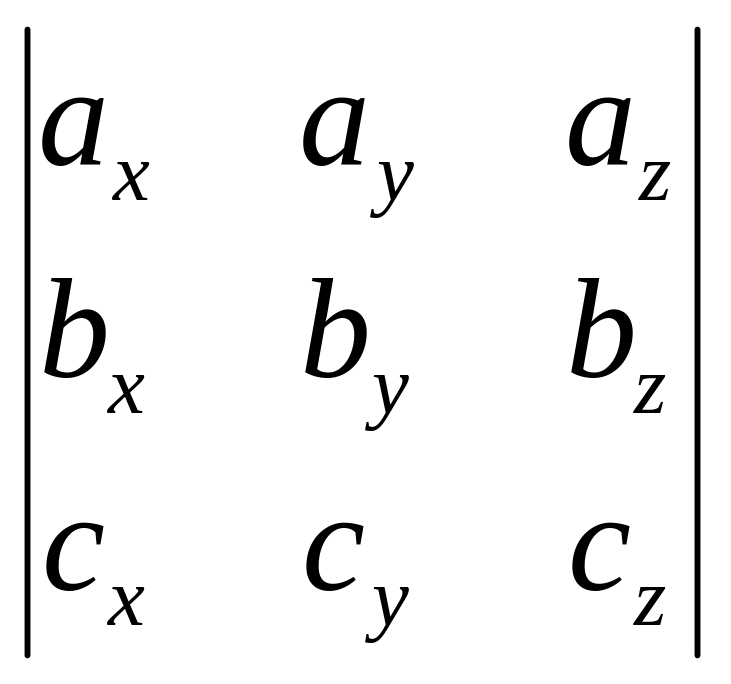Замечание. Использование определителя третьего порядка позволяет упростить и запись векторного произведения. Его можно представить в виде:

 = .

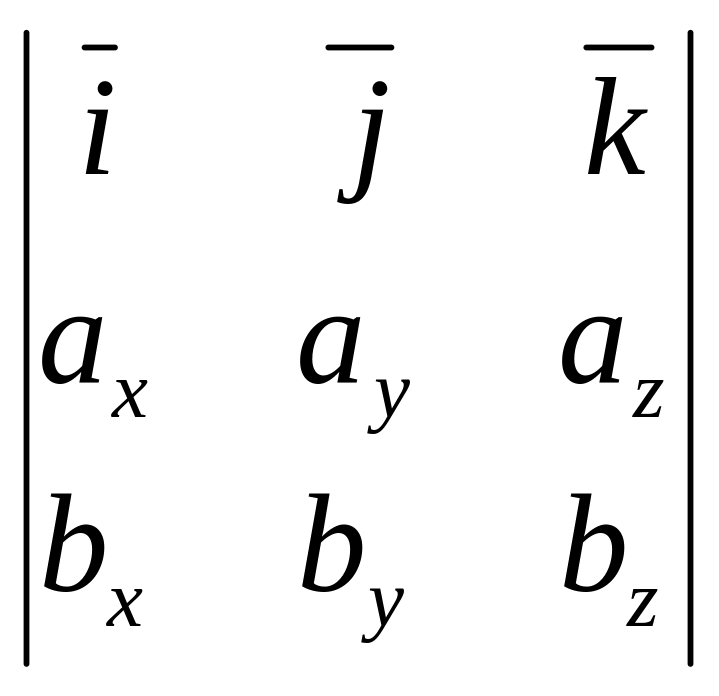Примеры. 1) Докажем, что векторы = (1;2;3),

= (4;5;6) и = (7;8;9) компланарны. Для этого найдем их смешанное произведение: = = 1^. – 2^. +3^. =1^.(45–48)–2^.(36–42)+3^.(32–35)= –3+12–9=0.

Значит, векторы компланарны, что и требовалось доказать.

2) Найдем объем параллелепипеда, построенного на векторах = (1;2;3), = (4;5;6) и = (0;1;–1), и определим, правую или левую тройку векторов они образуют. Смешанное произведение векторов =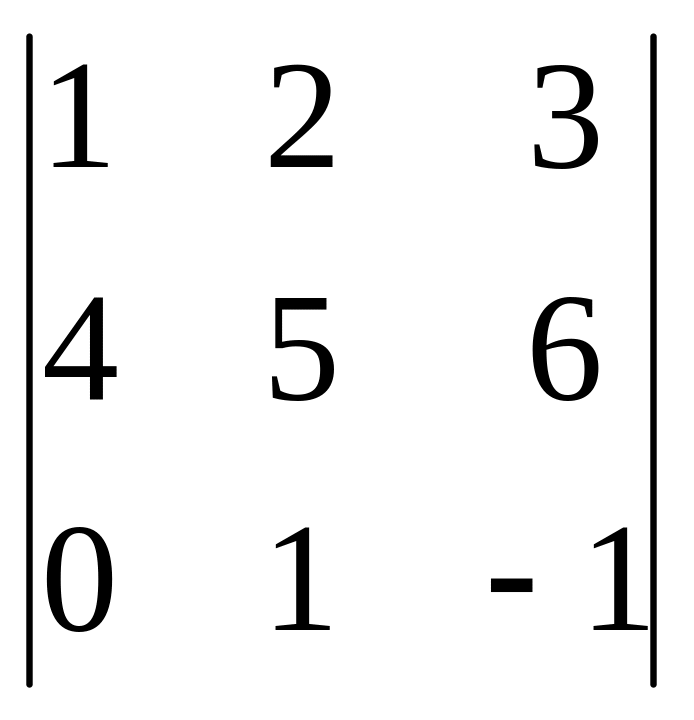 = 1^. – 2^. +3^. =1^.(–5–6)–2^.(–4–0)+3^.(4–0) =

–11+8+12 = 9. Значит, > 0, поэтому векторы образуют правую тройку. Объем параллелепипеда равен  = 9= 9. 