3.6. Поверхности второго порядка

Поверхность второго порядка – это множество точек пространства, координаты которых удовлетворяют уравнению вида:

a₁₁x²+a₂₂y²+a₃₃z²+2a₁₂xy+2a₁₃xz+2a₂₃yz+2a₁x+2a₂y+2a₃z+a_o=0, где коэффициенты a₁₁, a₂₂, a₃₃, a₁₂, a₁₃ и a₂₃ одновременно не равны нулю. С помощью преобразований системы координат любое такое уравнение приводится к одному из семнадцати следующих видов.

1^о. – эллипсоид.

2^о. – «мнимый» эллипсоид

(уравнению не удовлетворяет ни одна точка).

3^о. – «мнимый» конус

(уравнению удовлетворяет только точка (0;0;0)).

4^о. – однополостный гиперболоид.

5^о. – двуполостный гиперболоид.

6^о. – конус.

7^о. – эллиптический параболоид.

8^о. – гиперболический параболоид.

9^о. – эллиптический цилиндр.

10^о. – «мнимый» цилиндр

(уравнению не удовлетворяет ни одна точка).

11^о. – пара «мнимых» плоскостей,

имеющих общую действительную прямую

(уравнению удовлетворяет только прямая х=0, у=0).

12^о. (или ) – гиперболический

цилиндр.

13^о. – пара пересекающихся плоскостей.

14^о. у² = 2рх – параболический цилиндр.

15^о. – пара параллельных плоскостей.

16^о. – пара «мнимых» плоскостей,

не имеющих общих точек

(уравнению не удовлетворяет ни одна точка).

17^о. – пара совпавших плоскостей.

Раздел II. Введение в анализ

1. Комплексные числа

1.1. Множество комплексных чисел

В школе изучаются четыре множества чисел: натуральные числа, целые числа, рациональные числа, действительные числа. Эти множества обозначаются соответственно N, Z, Q, R. Напомним, что представляют собой эти множества.

Множество N – это множество чисел, используемых при счете: N = {1; 2; 3; …}. Сумма и произведение натуральных чисел – всегда натуральное число, разность и частное – не всегда. Говорят, что на множестве N определены операции сложения и умножения.

Множество Z получается, если к натуральным числам добавить числа, противоположные натуральным, и число нуль: Z = {… –2; –1; 0; 1; 2; …}. Сумма, произведение и разность целых чисел – всегда целое число, а частное – не всегда. На множестве Z определены операции сложения, умножения и вычитания.

Множество Q состоит из дробей с целым числителем и натуральным знаменателем: Q = { : mZ, nN}. Сумма, произведение, разность и частное (если делитель – не нуль) рациональных чисел – всегда рациональное число. На множестве Q определены операции сложения, умножения, вычитания и деления.

Множество R состоит из всех чисел, которые можно изобразить точками числовой прямой. На этой прямой есть точки, не занятые рациональными числами: например, точка, изображающая длину диагонали единичного квадрата. Числа, соответствующие этим точкам, называются иррациональными; множество R состоит из всех рациональных чисел и из всех иррациональных чисел. Сумма, произведение, разность и частное (если делитель – не нуль) действительных чисел – всегда действительное число. На множестве R определены операции сложения, умножения, вычитания и деления. Множество R отличается от множества Q, например, тем, что все квадратные корни из неотрицательных рациональных чисел являются действительными числами (но не все являются рациональными).

Соотношение между перечисленными числовыми множествами выглядит так: NZQR. Оказывается, можно построить такое расширение множества R с сохранением операций, в котором существуют квадратные корни из отрицательных действительных чисел. Это расширение обозначается С и называется множеством комплексных чисел. Элементами множества С (то есть комплексными числами) являются двучлены вида a+bi, где a и b – действительные числа. Сложение и умножение комплексных чисел выполняются так же, как сложение и умножение любых двучленов, но выражение i² всякий раз заменяется числом –1. Таким образом,

(a+bi)+(c+di) = (a+c)+(b +d)i;

(a+bi)(c+di) = (ac–bd)+(ad +bc)i.

Если обозначить комплексное число a+bi буквой z: z=a+bi, то число а называется действительной частью числа z (обозначение: а = Rez), а число b – его мнимой частью (обозначение: b = Imz). Число 0+0i будем обозначать просто 0, а число 1+0i – просто 1. Если z=a+bi, то число –a–bi будем обозначать –z (противоположное число). Если z0, то число будем обозначать (обратное число).

Можно доказать, что сложение и умножение комплексных чисел обладают теми же свойствами, что и сложение и умножение действительных чисел. Перечислим эти свойства.

1. z₁+z₂ = z₂+z₁. 5. z₁z₂ = z₂z₁.

2. z₁+(z₂+z₃) = (z₁+z₂)+z₃. 6. z₁(z₂z₃) = (z₁z₂)z₃.

3. z+0 = z. 7. z^.1 = z.

4. z+(– z) = 0. 8. z( ) = 1, z0.

9. z₁(z₂+z₃) = z₁z₂+z₁z₃.

Таким образом, i = 0+0i – комплексное число, квадрат которого равен –1:

i²= –1.

Число i называют мнимой единицей, а число вида bi, действительная часть которого равна нулю, называют чисто мнимым числом.

Теперь можно считать, что всякое действительное число a является комплексным числом a+0i, поэтому RC. В множестве С уравнение x² = a, где a<0, имеет два корня: i и –i , то есть существует квадратные корни из отрицательных действительных чисел. Отсюда получаем формулу корней квадратного уравнения действительными коэффициентами и отрицательным дискриминантом:

если ax²+bx+c=0, D<0, то х_1,2= .

Операции вычитания и деления в множестве С определяются так:

z₁–z₂ = z₁+(–z₂); z₁:z₂ = z₁^.( ), если z₂0.

Итак в множестве С выполнимы все четыре операции, определенные в множестве R.

Примеры. 1) Найдем значение выражения:

(2–3i)–(1–4i)(–5+3i).

Имеем: (2–3i)–(1–4i)(–5+3i) = (2–3i)–(–5+20i+3i–12i²) = (2–3i)–(–5+23i+12) = (2–3i)–(7+23i) = –5–26i.

2) Найдем значение выражения: (2–3i)²–(1–4i)(1+4i)+(1–i)³.

Заметим, что поскольку все свойства сложения и умножения сохраняются на множестве С, то и формулы сокращенного умножения справедливы. Воспользуемся ими:

(2–3i)²–(1–4i)(1+4i)+(1–i)³ = (2²–2^.2^.3i+(3i)²)–(1²–(4i)²)+

+(1³–3^.1^2.i+3^.1^.i²–i³) = (4–12i–9)–(1+16)+(1–3i–3+i) =

= –13–12i–17–2–2i = –32–14i.

3) Найдем значение выражения: .

Домножим числитель и знаменатель этой дроби на число 1–2i: = = =

= = –1–2i.

Замечание. В этом примере мы домножили числитель и знаменатель дроби со знаменателем 1+2i на число 1–2i. Комплексные числа, которые отличаются только знаком мнимой части, называются комплексно сопряженными. Число, комплексно сопряженное с числом z, обозначается Таким образом, 1–2i = . Вообще при делении комплексных чисел удобно записать частное в виде дроби, а затем домножить числитель и знаменатель на число, комплексно сопряженное знаменателю.

4) Решим уравнение: z² = 3–4i. Пусть z = x+yi. Тогда (x+yi)²= 3–4i, то есть x²+2хyi+(уi)² = 3–4i, или (х²–у²)+2хуi = =3–4i. Приравняв действительные и мнимые части равных чисел, получим систему: , откуда 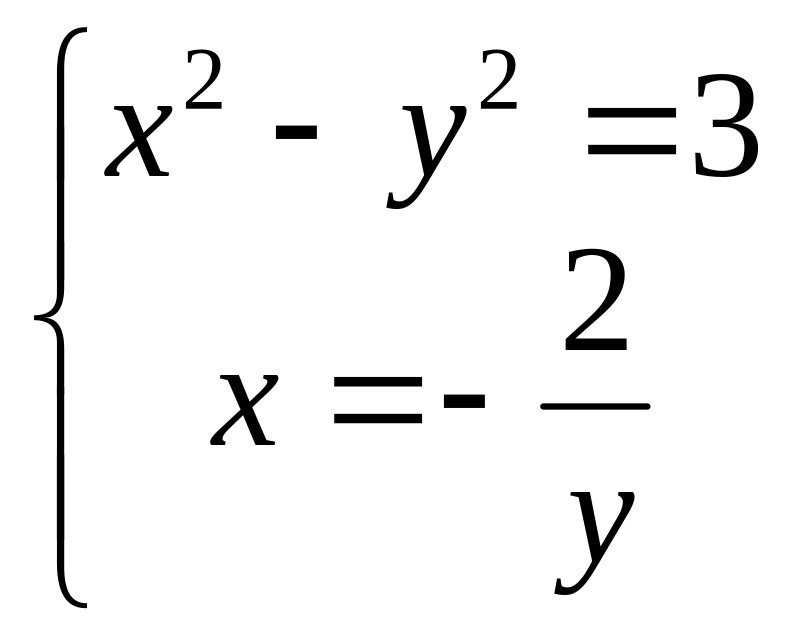. Подставим полученное выражение для х в первое уравнение и решим его: ; ; ; у⁴+3у²–4=0; (у²–1)(у²+4)=0; поскольку у – действительное число, то у²+40, то есть у²–1=0; у₁ = 1, у₂= –1, х₁= –2, х₂ = 2. Получаем два корня исходного уравнения: z₁= –2+i, z₂= 2–i.

5) Решим квадратное уравнение: 9х²–12х+29=0. Имеем: D=(–12)²–4^.9^.29=144–1044= –900<0. Поэтому можно применить формулу х_1,2= . Тогда х_1,2= = = = ; х₁ = ; х₂ = . Заметим, что формулы Виета для корней квадратного уравнения справедливы и в этом случае: х₁+х₂ = и х₁х₂ = – то есть х₁+х₂ = – и х₁х₂ = .