
- •Часть 1
- •Раздел I. Элементы аналитической геометрии
- •1. Векторы на плоскости и в пространстве
- •1.1. Основные понятия
- •1.2. Линейные операции над векторами
- •1.3. Проекция вектора на ось
- •1.4. Базисы плоскости и пространства
- •1.5. Прямоугольная декартова система координат
- •1.6. Координаты вектора в прямоугольной декартовой
- •1.7. Скалярное произведение векторов
- •3. Скалярные квадраты базисных ортов равны 1, а их попарные скалярные произведения равны нулю.
- •1.8. Векторное произведение векторов
- •3. Попарные произведения базисных ортов вычисляются по формулам:
- •1.9. Смешанное произведение векторов
- •2. Линии на плоскости
- •2.1. Общее уравнение прямой на плоскости
- •2.2. Различные виды уравнения прямой на плоскости
- •2.3. Взаимное расположение двух прямых на плоскости
- •2.4. Расстояние от точки до прямой на плоскости
- •2.5. Эллипс, гипербола, парабола
- •2.6. Преобразование координат на плоскости
- •2.7. Общее уравнение кривой второго порядка
- •4О. (или ) – гипербола.
- •2.8. Полярные координаты на плоскости
- •3. Линии и поверхности в пространстве
- •3.1. Уравнение плоскости
- •3.2. Угол между плоскостями.
- •3.3. Уравнения прямой в пространстве
- •3.4. Угол между прямыми в пространстве.
- •3.5. Взаимное расположение двух прямых
- •3.6. Поверхности второго порядка
- •Раздел II. Введение в анализ
- •1. Комплексные числа
- •1.2. Тригонометрическая форма комплексного числа
- •2. Обзор элементарных функций
- •2.1. Простейшие функции
- •2.2. Степенные функции
- •2.3. Показательные и логарифмические функции
- •2.4. Тригонометрические функции
- •2.4. Обратные тригонометрические функции
- •3. Пределы
- •3.1. Предел числовой последовательности
- •3.3. Предел функции в точке
- •3.4. Непрерывность функции
- •Часть 1
- •127994, Москва, ул. Образцова, 15
3.3. Предел функции в точке
Определение 1. Функция f(x), определенная в некоторой проколотой окрестности точки a, называется бесконечно малой при х, стремящемся к а (пишут: ха), если для любого положительного числа существует такая проколотая окрестность точки а, что при всех х, принадлежащих этой окрестности, f(x)<.
Пример. Функция f(x)=х–а является бесконечно малой при ха. Действительно, если >0, то в проколотой -окрестности точки а будет f(x)<.
Свойства функций, бесконечно малых в точке, аналогичны свойствам бесконечно малых последовательностей. Перечислим эти свойства.
1о. Если постоянная функция f(x)=С является бесконечно малой при ха, то С=0.
2о. Сумма двух функций, бесконечно малых при ха, является бесконечно малой функцией при ха.
3о. Если функция f(x) – бесконечно малая при ха и существует такая проколотая окрестность точки а, в которой g(x)f(x), то функция g(x) – бесконечно малая при ха.
4о. Если функция f(x) – бесконечно малая при ха, то f(x) ограничена в некоторой проколотой окрестности точки а (это значит, что существует такое число М, что в этой проколотой окрестности f(x)М).
5о. Если функция f(x) – бесконечно малая при ха, а функция g(x) ограничена в некоторой проколотой окрестности точки а, то функция f(x)g(x) – бесконечно малая при ха.
Следствие 1. Если функция f(x) – бесконечно малая при ха, то для любого числа С функция Сf(x) – бесконечно малая при ха.
Следствие 2. Произведение двух функций, бесконечно малых при ха, является бесконечно малой функцией при ха.
Определение 2. Число b называется пределом функции f(x) при х а, если функция f(x)–b является бесконечно малой при х а.
Обозначение предела функции в точке:
b
=![]() .
.
Из определения вытекают следующие утверждения:
1)если функция f(x) – бесконечно малая при ха, то =0;
2)
![]() =С;
=С;
3)
![]() =а;
=а;
4) если =b и b<0, то существует такая проколотая окрестность точки а, в которой f(x)<0; аналогичное утверждение справедливо и при b>0.
Свойства предела функции в точке сформулируем в виде теорем, аналогичных теоремам 1-5 предыдущего пункта.
Теорема 1 (о единственности предела). Если =b и =c, то c = b.
Теорема 2 (об ограниченности функции, имеющей предел в точке). Если =b, то существует такая проколотая окрестность точки а, в которой функция ограничена.
Теорема 3 (о переходе
к пределу в неравенстве). Если
=b
и
![]() =с,
причем f(x)g(x)
в некоторой проколотой окрестности
точки а, то bс.
=с,
причем f(x)g(x)
в некоторой проколотой окрестности
точки а, то bс.
Следствие. Если =b, причем f(x)0 в некоторой проколотой окрестности точки а, то b0. Если =b, причем f(x)0 в некоторой проколотой окрестности точки а, то b0.
Теорема 4 (о
промежуточной функции). Если
=b
и
=b,
причем f(x)h(x)g(x)
в некоторой проколотой окрестности
точки а, то
![]() =b.
=b.
Теорема 5 (об арифметических операциях с пределами).
1)
Если
=b
и
=с,
то
![]() =
b+c.
=
b+c.
2)
Если
=b
и
=с,
то![]() =bc.
=bc.
Следствие. Если
=b,
то
![]() =Cb.
=Cb.
3)
Если
=b,
причем b0,
то
![]() =
=![]() .
.
Следствие.
Если
=b
и
=с,
причем c0,
то
![]() =
=![]() .
.
Примеры.
1) Найдем
![]() :
=
:
=
=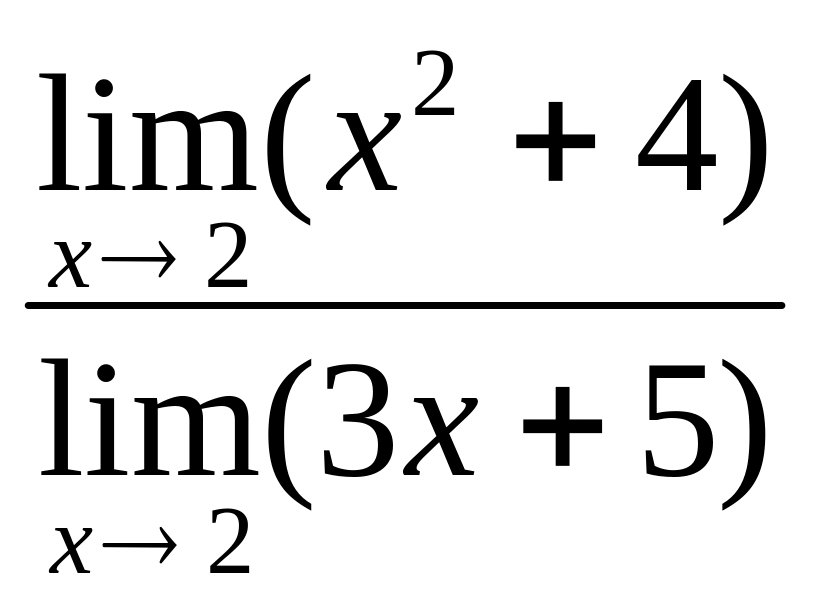 =
=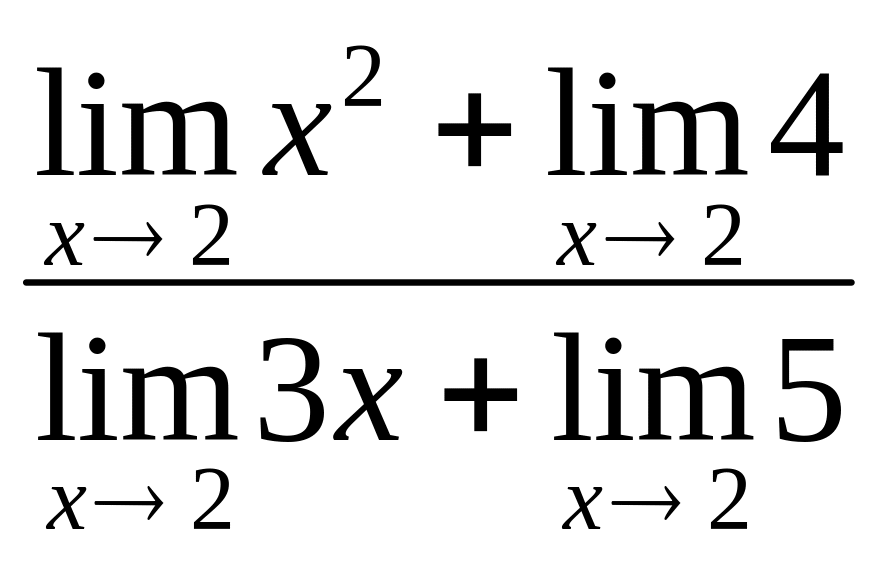 =
=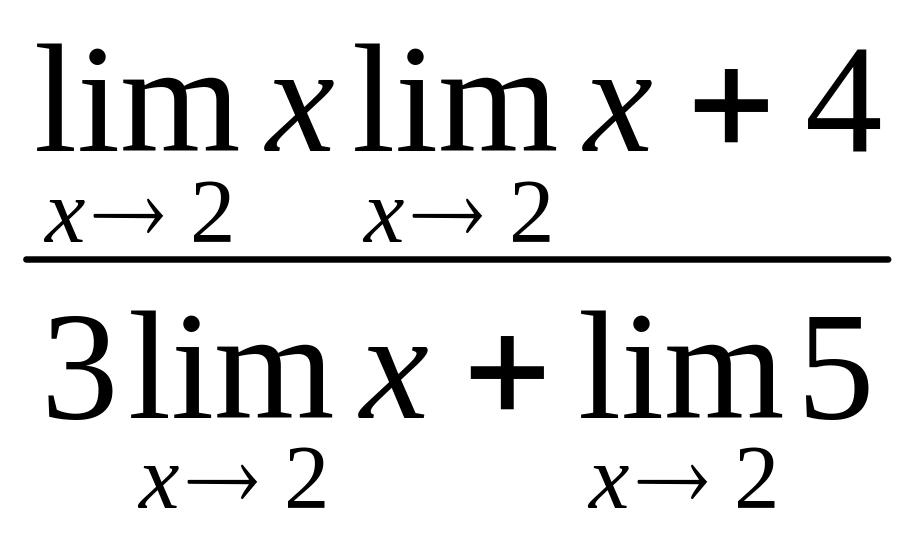 =
=![]() =
=![]() .
.
2) Найдем
![]() .
Если, как в предыдущем примере, попробовать
сразу применить теорему о пределе
частного, то получится выражение
.
Если, как в предыдущем примере, попробовать
сразу применить теорему о пределе
частного, то получится выражение
![]() ;
значит, надо сначала преобразовать
данное выражение. Для этого разложим
числитель и знаменатель дроби на
множители:
=
;
значит, надо сначала преобразовать
данное выражение. Для этого разложим
числитель и знаменатель дроби на
множители:
=![]() .
Поскольку при вычислении предела мы
рассматриваем функцию только в проколотой
окрестности точки 3, то есть х3,
то выражение (х–3) отлично от нуля,
поэтому дробь можно сократить:
=
.
Поскольку при вычислении предела мы
рассматриваем функцию только в проколотой
окрестности точки 3, то есть х3,
то выражение (х–3) отлично от нуля,
поэтому дробь можно сократить:
=![]() .
А теперь можно применить теорему о
пределе частного:
=
.
А теперь можно применить теорему о
пределе частного:
=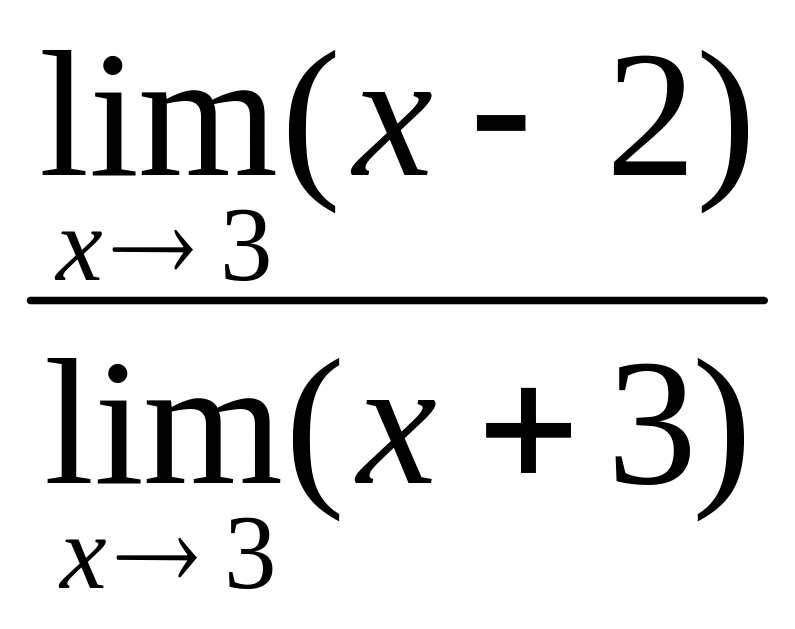 =
=
= =
=![]() =
=![]() .
Заметим, что если, как в приведенном
примере,
=
=0,
то предел вида
называется неопределенностью вида
нуль на нуль и обозначается так:
=
.
Заметим, что если, как в приведенном
примере,
=
=0,
то предел вида
называется неопределенностью вида
нуль на нуль и обозначается так:
=![]() .
Вычисление предела такого вида называется
раскрытием неопределенности.
.
Вычисление предела такого вида называется
раскрытием неопределенности.
Определение 3.
Число b называется
пределом функции f(x)
при х, стремящемся к а слева (пишут:
ха–0) , если
функция f(x)–b
является бесконечно малой при ха,
где х<а. Число b
называется пределом функции f(x)
при х, стремящемся к а справа (пишут:
ха+0), если
функция f(x)–b
является бесконечно малой при ха,
где х>а. Пределы слева и справа
называют односторонними пределами
функции f(x)
при ха и
обозначают соответственно
![]() и
и
![]() или,
короче, f(a–0)
и f(a+0).
или,
короче, f(a–0)
и f(a+0).
Замечание. Из определения следует, что предел функции в точке существует тогда и только тогда, когда оба односторонних предела существуют и равны между собой.
Пример. Рассмотрим
функцию f(x)=![]() .
.
![]() =
=![]() =
=![]() =
32–2.3+1=4;
=
32–2.3+1=4;
![]() =
=![]() =
2.3–1=5; таким образом, односторонние
пределы не совпадают, поэтому
=
2.3–1=5; таким образом, односторонние
пределы не совпадают, поэтому
![]() не существует.
не существует.
Определение 4.
Функция f(x)
называется бесконечно большой при
ха, если
функция
![]() является
бесконечно малой при ха.
Это записывают так:
=
. Аналогично
определяется функция, бесконечно большая
при ха–0
или при ха+0.
является
бесконечно малой при ха.
Это записывают так:
=
. Аналогично
определяется функция, бесконечно большая
при ха–0
или при ха+0.
Пример. Поскольку
![]() =
=
![]() =0,
то функция f(x)
=
=0,
то функция f(x)
=
![]() –
бесконечно малая при х1.
Значит, функция f(x)
=
–
бесконечно малая при х1.
Значит, функция f(x)
=
![]() –
бесконечно большая при х1:
–
бесконечно большая при х1:
![]() =.
=.
Замечание.
=
тогда и только тогда, когда прямая х=а
является вертикальной асимптотой
графика функции у=f(x).
Например, график дробно-линейной функции
у=![]() имеет, как мы знаем, вертикальную
асимптоту х = –3.
имеет, как мы знаем, вертикальную
асимптоту х = –3.
Важные примеры.
1)
Рассмотрим
![]() .
Так как sin0=0, то
–
неопределенность
.
Будем рассматривать данную функцию на
промежутке (
.
Так как sin0=0, то
–
неопределенность
.
Будем рассматривать данную функцию на
промежутке (![]() ;
;![]() ).
А так как данная функция четная, то можно
считать, что 0<x<
.
Возьмем числовую окружность с центром
в начале координат О; пусть А(1;0), Р(cosx;
sinx),
B(cosx;
0), C(1;tgx).
Рассмотрим СОА и
сектор РОА, длина дуги которого равна
х. Площадь сектора равна
).
А так как данная функция четная, то можно
считать, что 0<x<
.
Возьмем числовую окружность с центром
в начале координат О; пусть А(1;0), Р(cosx;
sinx),
B(cosx;
0), C(1;tgx).
Рассмотрим СОА и
сектор РОА, длина дуги которого равна
х. Площадь сектора равна
![]() ,
а площадь СОА равна
,
а площадь СОА равна
![]() .
Так как треугольник содержит сектор,
то получаем, что x<tgx.
С другой стороны, длина дуги РА (равная
х) больше длины хорды РА, которая, в свою
очередь, больше длины отрезка РВ (так
как РВ – катет, а РА – гипотенуза
прямоугольного треугольника РАВ). Так
как РВ = sinx,
то получаем, что sinx<x.
Итак, справедливо двойное неравенство:
sinx<x<tgx.
Отсюда 1<
.
Так как треугольник содержит сектор,
то получаем, что x<tgx.
С другой стороны, длина дуги РА (равная
х) больше длины хорды РА, которая, в свою
очередь, больше длины отрезка РВ (так
как РВ – катет, а РА – гипотенуза
прямоугольного треугольника РАВ). Так
как РВ = sinx,
то получаем, что sinx<x.
Итак, справедливо двойное неравенство:
sinx<x<tgx.
Отсюда 1<![]() <
<![]() .
Поскольку
.
Поскольку
![]() =
=![]() =1,
то по теореме о промежуточной функции
=1,
то по теореме о промежуточной функции
![]() =1,
а значит,
=1,
а значит,
=1.
Это равенство
называют первым замечательным пределом
и используют для раскрытия неопределенностей.
Например, воспользовавшись равенством
![]() =
=![]() ,
получим:
,
получим:
![]() =1.
А если в первом замечательном пределе
заменить x на arcsinx,
а sinx –
на х, получим:
=1.
А если в первом замечательном пределе
заменить x на arcsinx,
а sinx –
на х, получим:
![]() =1.
Аналогично
=1.
Аналогично
![]() =1.
Например,
=1.
Например,
![]() =
=![]() =
=![]() =
=![]() =
=![]() ;
;![]() =
=
=
= =
=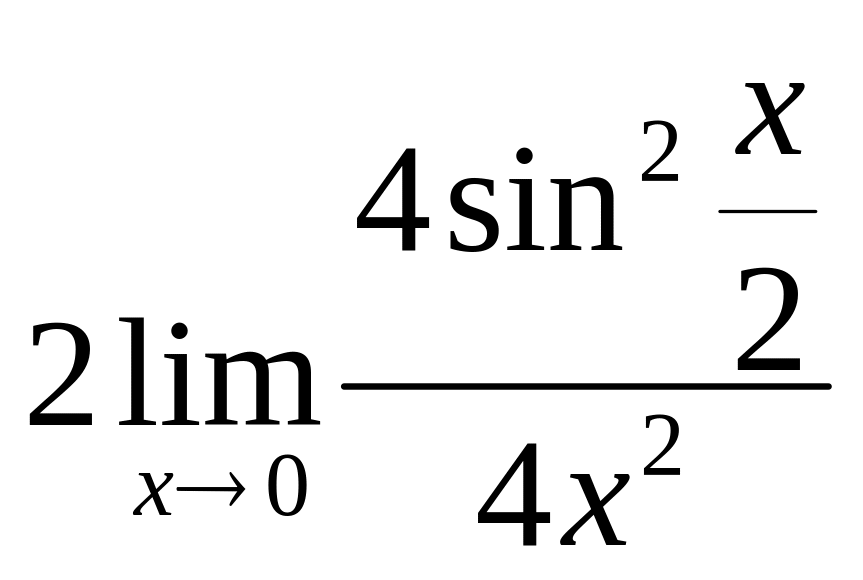 =
= =
=
= =
=![]() =
.
=
.
2)
Если функции f(x)
и g(x)
являются бесконечно малыми при ха
и
![]() =1,
то функции называются эквивалентными
бесконечно малыми при ха:
f(x)g(x).
Если f(x)f1(x)
и g(x)g1(x)
при ха, то
=1,
то функции называются эквивалентными
бесконечно малыми при ха:
f(x)g(x).
Если f(x)f1(x)
и g(x)g1(x)
при ха, то
![]() =
=
=
=![]() =
=![]() =
=![]() .
Это значит, что при вычислении пределов
можно бесконечно малые множители
заменять на эквивалентные.
.
Это значит, что при вычислении пределов
можно бесконечно малые множители
заменять на эквивалентные.
Если
(х) – бесконечно
малая при х0, то
sin((х))
(х), arcsin((х))
(х), tg((х))
(х), arctg((х))
(х), 1–cos((х))
0,5((х))2. С
помощью этих основных эквивалентностей
получаем, например:
![]() =
=
=
=![]() =
=![]() =
=![]() =
.
=
.
3)
Если
![]() =1,
=1,
![]() =,
то
=,
то
![]() – неопределенность [1].
Для раскрытия таких неопределенностей
используют второй замечательный предел:
пусть f(x)=1+(х),
где (х) –
бесконечно малая при х;
тогда
=
– неопределенность [1].
Для раскрытия таких неопределенностей
используют второй замечательный предел:
пусть f(x)=1+(х),
где (х) –
бесконечно малая при х;
тогда
=
![]() =
=![]() =
=
=![]() =
=![]() .
Например,
.
Например,
![]() =
=
=![]() =
=![]() =
e3;
=
e3;
![]() =
=
=![]() =
=![]() =
=![]() ==е4.
==е4.
Из
формулы
![]() =е
получаем:
=е
получаем:
![]() =1,
– то есть ln(1+x)x
при х0; отсюда
ex–1x
при х0; ax–1
=1,
– то есть ln(1+x)x
при х0; отсюда
ex–1x
при х0; ax–1
xlna
при х0; (1+x)k–1kx
при х0. Используя
эти эквивалентности, получим:
![]() =
=![]() =
=![]() =
;
=
;
![]() =
=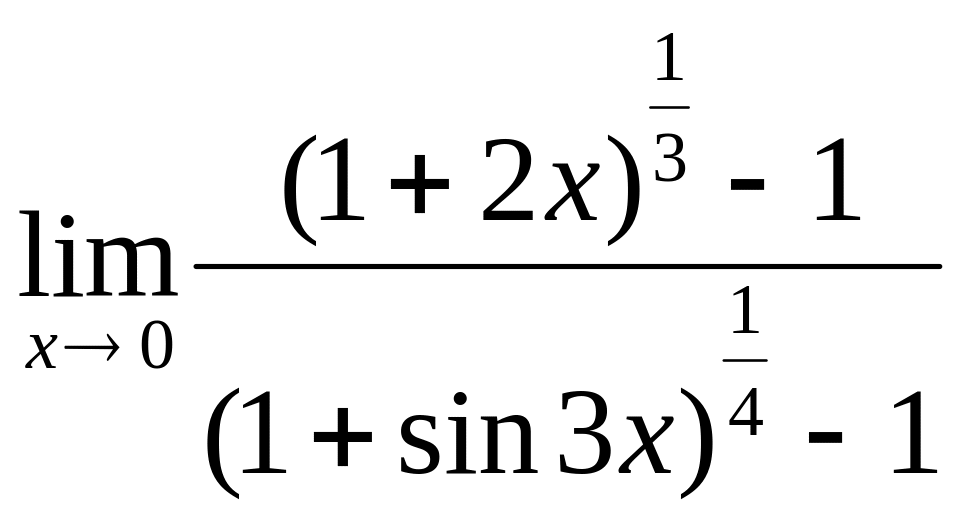 =
= =
=![]() =
=![]() =
.
=
.
4)
Вычислим
![]() .
Обозначим х–4=9у. Тогда
=
.
Обозначим х–4=9у. Тогда
=![]() =
=![]() =
= =
=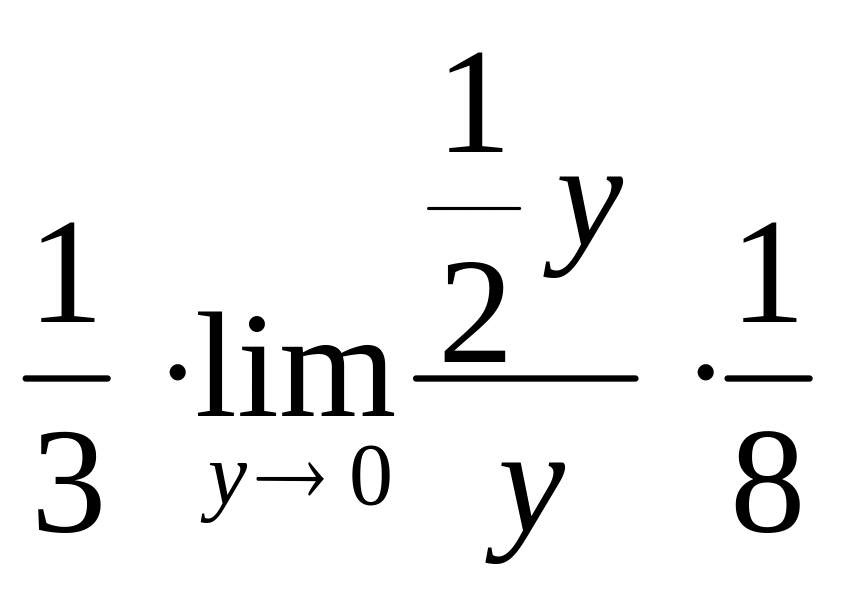 =
=![]() =
=![]() .
.
