3. Пределы

3.1. Предел числовой последовательности

Числовой последовательностью будем называть функцию f(n), определенную на множестве N натуральных чисел. Значение f(n) принято обозначать через a_n, а саму последовательность записывают в виде (a_n): (a_n)=(a₁, a₂, ...). Число a_n будем называть n-ым членом последовательности.

Числовая последовательность (a_n) называется ограниченной снизу, если все ее члены не меньше некоторого числа: a_nМ при всех n.

Числовая последовательность (a_n) называется ограниченной сверху, если все ее члены не больше некоторого числа: a_nМ при всех n.

Числовая последовательность (a_n) называется ограниченной, если все ее члены по модулю не больше некоторого числа: a_nМ при всех n. Очевидно, что числовая последовательность является ограниченной тогда и только тогда, когда она является ограниченной снизу и ограниченной сверху.

Числовая последовательность (a_n) называется возрастающей, если каждый следующий ее член больше предыдущего: a_n+1>a_n при всех n. Если строгое неравенство заменить нестрогим, то последовательность называется неубывающей.

Числовая последовательность (a_n) называется убывающей, если каждый следующий ее член меньше предыдущего: a_n+1<a_n при всех n. Если строгое неравенство заменить нестрогим, то последовательность называется невозрастающей.

Числовая последовательность называется монотонной, если она является возрастающей, убывающей, невозрастающей или неубывающей. Иногда возрастающие и убывающие последовательности называют строго монотонными.

Определение 1. Числовая последовательность (a_n) называется бесконечно малой, если для любого положительного числа  существует такое число N, зависящее от , что при всех n, больших N, a_n<.

Другими словами, какой бы интервал (–;) мы ни взяли, все члены последовательности, начиная с некоторого номера, попадают в этот интервал.

Примеры. 1) Пусть a_n= . Докажем, что эта последовательность является бесконечно малой.

Пусть >0. Для того, чтобы выполнялось неравенство a_n<, нужно, чтобы было <. Отсюда 1<n. Поскольку >0, получаем: n> . Возьмем N=N()= . Тогда, если n>N, то n> , <, то естьa_n<.

Итак, для любого положительного числа  мы нашли такое число N, зависящее от , что при всех n, больших N, a_n<. Это и означает, что последовательность (a_n) является бесконечно малой, что и требовалось доказать.

2) Пусть a_n= . Докажем, что эта последовательность является бесконечно малой.

Пусть >0. Для того, чтобы выполнялось неравенство a_n<, нужно, чтобы было <. Отсюда 2<3n+, то есть 2–<3n. Поскольку >0, получаем: n> . Возьмем N=N()= . Тогда, если n>N, то n> , 3n>2–, (3n+1)>2, <, то естьa_n<.

Итак, для любого положительного числа  мы нашли такое число N, зависящее от , что при всех n, больших N, a_n<. Это и означает, что последовательность (a_n) является бесконечно малой, что и требовалось доказать.

Свойства бесконечно малых последовательностей.

1^о. Если бесконечно малая последовательность (a_n) – постоянная, то a_n=0 при всех n.

 Действительно, пусть a_n=С при всех n и С0. Возьмем =С>0. Так как (a_n) – бесконечно малая, то существует N такое, что если n>N, то a_n<, то есть С<С. Так как последнее неравенство невозможно, то исходное предположение неверно, поэтому С=0, что и требовалось доказать. 

2^о. Если последовательности (a_n) и (b_n) – бесконечно малые, то последовательность (с_n), где с_n = a_n+b_n, – тоже бесконечно малая.

 Пусть >0. Возьмем ₁= >0. Так как (a_n) – бесконечно малая, то существует N₁ такое, что если n>N₁, то a_n<₁, то есть a_n< . Так как (b_n) – бесконечно малая, то существует N₂ такое, что если n>N₂, то b_n<₁, то есть b_n< . Пусть N – наибольшее из чисел N₁ и N₂. Тогда, если n>N, то n>N₁ и n>N₂, поэтому a_n< и b_n< . С другой стороны, с_n=а_n+b_n. Поскольку модуль суммы двух чисел не превосходит суммы их модулей, то получаем: с_n=а_n+b_nа_n+b_n, а значит, если n>N, то с_nа_n+b_n< + =. Итак, для произвольного >0 мы нашли такое число N, что при всех n, больших N, c_n<. Значит, последовательность (c_n) является бесконечно малой, что и требовалось доказать. 

3^о. Если последовательность (b_n) – бесконечно малая и a_nb_nпри всех n, то последовательность (a_n) – тоже бесконечно малая.

 Пусть >0. Так как (b_n) – бесконечно малая, то существует N такое, что если n>N, то b_n<. Так как a_nb_nпри всех n, то при n>N получаем, что a_nb_n<. Итак, для произвольного >0 существует такое N, что при всех n, больших N, а_n<. Значит, последовательность (а_n) является бесконечно малой, что и требовалось доказать. 

4^о. Если последовательность (а_n) – бесконечно малая, то последовательность (a_n) – ограниченная.

 Возьмем, например, =1. Так как (а_n) – бесконечно малая, то существует N такое, что если n>N, то а_n<1. Из всех членов последовательности, номера которых не больше N, выберем наибольшее по модулю и обозначим этот модуль через А. Тогда, если nN, то а_nА, а если n>N, то а_n<1. Пусть М=А+1. Тогда при всех n получаем, что а_nМ. Значит, последовательность (а_n) является ограниченной, что и требовалось доказать. 

5^о. Если последовательность (a_n) – бесконечно малая, а последовательность (b_n) – ограниченная, то последовательность (с_n), где с_n= a_nb_n, – бесконечно малая.

 Так как последовательность (b_n) – ограниченная, то существует такое число М>0, что b_nМ при всех n. Пусть >0. Возьмем ₁= >0. Так как (a_n) – бесконечно малая, то существует N такое, что если n>N, то a_n<₁, то есть a_n< . Тогда с_n=а_nb_n=а_n^.b_n< ^.М =. Итак, для произвольного >0 существует такое N, что при всех n, больших N, c_n<. Значит, последовательность (c_n) является бесконечно малой, что и требовалось доказать. 

Следствие 1. Если последовательность (a_n) – бесконечно малая, то для любого числа С последовательность (Са_n) – бесконечно малая.

Следствие 2. Если последовательности (a_n) и (b_n) – бесконечно малые, то последовательность (с_n), где с_n = a_nb_n, – тоже бесконечно малая.

Определение 2. Число а называется пределом числовой последовательности (a_n), если последовательность (b_n), где b_n=а_n–а, является бесконечно малой.

Обозначение предела числовой последовательности: а = .

Из определения следует, что предел бесконечно малой последовательности равен нулю, а предел постоянной последовательности а_n=а равен а.

Последовательность, имеющую предел, называют сходящейся, не имеющую предела – расходящейся.

Пример. Пусть a_n= . Докажем, что предел а этой последовательности равен . Для этого рассмотрим разность а_n–а = – = = . Обозначим b_n = и докажем, что последовательность (b_n) – бесконечно малая.

Пусть >0. b_n<, если <. Отсюда 1<9n+3, 9n>1–3, n> . Возьмем N= . Тогда, если n>N, то b_n<. Значит, последовательность (b_n) – бесконечно малая. Отсюда следует, что = , что и требовалось доказать. 

Замечание. Назовем -окрестностью числа а интервал (а–;а+). Тогда число а является пределом последовательности (a_n), если в любую -окрестность числа а попадают все члены последовательности, начиная с некоторого номера. Заметим, что объединение (а–;а)(а;а+) называют проколотой -окрестностью.

Свойства сходящихся последовательностей сформулируем в виде теорем.

Теорема 1 (о единственности предела). Если =а и =b, то а = b.

 Пусть а  b. Обозначим через . Тогда >0, а значит, начиная с некоторого номера N₁, все члены последовательности попадают в -окрестность числа а, а начиная с некоторого номера N₂, все члены последовательности попадают в -окрестность числа b. Поэтому, если N=N₁+N₂, то все члены последовательности с номерами, большими N, попадают в пересечение указанных -окрестностей. Но эти окрестности не пересекаются. Полученное противоречие показывает, что исходное предположение неверно, а значит, а  b, что и требовалось доказать.

Теорема 2 (об ограниченности сходящейся последовательности). Если числовая последовательность имеет предел, то она ограничена.

 Пусть =а. Тогда последовательность (b_n), где b_n=а_n–а, является бесконечно малой. Значит (по четвертому свойству бесконечно малых последовательностей), последовательность (b_n) ограничена: b_nМ при всех n. Тогда а_n=b_n+аb_n+aМ+a. Обозначив М₁=М+a, получим, что а_nМ+a при всех n. Значит, последовательность (а_n) ограничена, что и требовалось доказать.

Теорема 3 (о переходе к пределу в неравенстве). Если =а и =b, причем a_nb_n при всех n, то ab.

 Пусть, наоборот, a>b. Обозначим через . Тогда существует такое N₁, что а_n(a–;a+) при всех n>N₁, и существует такое N₂, что b_n(b–;b+) при всех n>N₂. Тогда, если n>N₁+N₂, то a–<a_n<a+. Но a– = a– = , поэтому a_n> . Аналогично, если n>N₁+N₂, то b–<b_n<b+. Но b+ = b+ = , поэтому b_n< . Итак, если n>N₁+N₂, то b_n< < a_n, что противоречит условию теоремы. Значит, предположение a>b неверно, поэтому ab, что и требовалось доказать.

Следствие. Если =а, причем a_n0 при всех n, то a0. Если =а, причем a_n0 при всех n, то a0.

Замечание. Заменить в этой теореме нестрогое неравенство строгим нельзя. Пусть, например, a_n = , b_n = . Тогда a_n <b_n при всех n, но = =0.

Теорема 4 (о промежуточной последовательности). Если =а и =а, причем a_nс_nb_n при всех n, то =а.

 Пусть >0. Тогда (см. доказательство предыдущей теоремы) существует такое N, что при n>N выполняются оба условия: а_n(a–;a+) и b_n(a–;a+). Тогда, если n>N, то a–<а_nc_nb_n<a+, то есть с_n(a–;a+) при всех n>N. Значит, =а, что и требовалось доказать. 

Теорема 5 (об арифметических операциях с пределами). 1) Если =а и =b, то =а+b.

 Это утверждение вытекает из второго свойства бесконечно малых последовательностей.

2) Если =а и =b, то =аb.

 Запишем разность а_nb_n–аb в виде: а_nb_n–аb=а_nb_n–а_nb +а_nb–аb. Отсюда а_nb_n–аb=а_n(b_n–b)+b(а_n–а). Здесь первое слагаемое – произведение членов ограниченной последовательности (а_n) и бесконечно малой последовательности (b_n–b). По пятому свойству бесконечно малых последовательностей последовательность (а_n(b_n–b)) является бесконечно малой. Аналогично бесконечно малой является и последовательность (b(а_n–а)). Значит, последовательность (а_nb_n–аb) является бесконечно малой и = аb, что и требовалось доказать.

Следствие. Если =а, то =Са.

3) Если =а, причем а0, то = .

 – = = ^. . Здесь первый множитель – член бесконечно малой последовательности. Поскольку а0, то положим = . Тогда, начиная с некоторого номера, a–<а_n<a+, откуда а_n>а–= . Тогда < , то есть последовательность ( ) ограничена. Значит, последовательность ( – ) – бесконечно малая, поэтому = , что и требовалось доказать. 

Следствие. Если =а и =b, причем b0, то = .

Примеры. 1) Найдем . Для этого разделим числитель и знаменатель дроби на n²:

= = =

= = = .

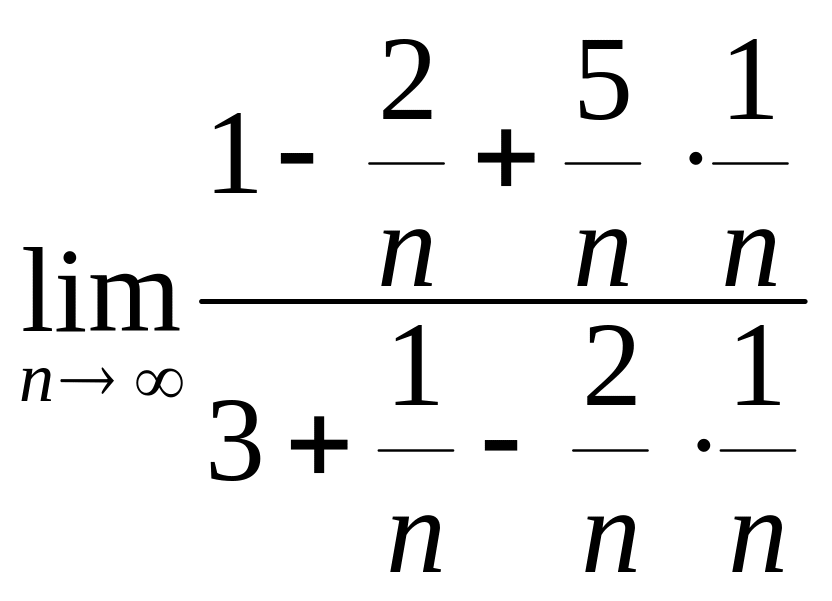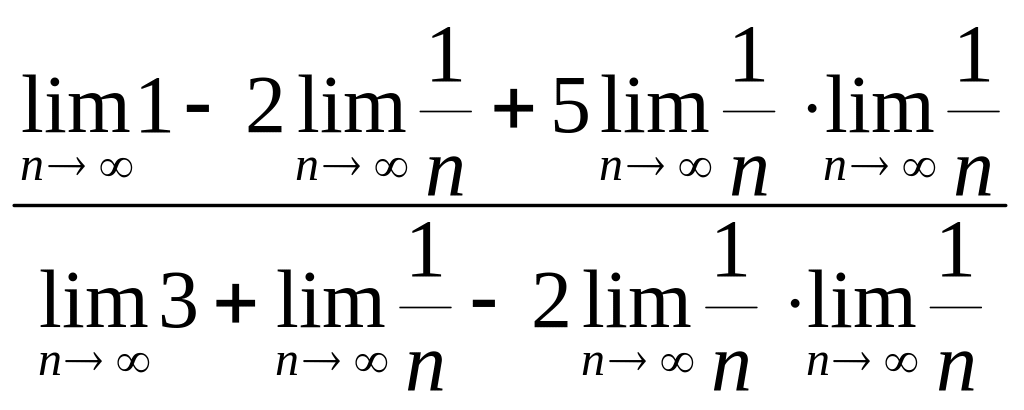2) Найдем . Для этого разделим числитель и знаменатель дроби на n²:

= = =

= = =0. 

Теорема 6 (об ограниченной монотонной последовательности). Если числовая последовательность возрастает и ограничена сверху (или убывает и ограничена снизу), то она сходится.

Эту теорему мы примем без доказательства.

Примеры. 1) Рассмотрим последовательность a_n=qⁿ, где q<1.

Если q = 0, то =0.

Если 0<q<1, то последовательность (qⁿ) убывает и ограничена снизу (qⁿ>0), поэтому имеет предел а. Тогда а= = = = . Отсюда получаем, что а=0.

Если –1<q<0, то последовательность (qⁿ), как мы показали, имеет предел равный нулю. А если =0, то и =0.

2) Рассмотрим последовательность b_n =b₁q^n–1, где q<1, – бесконечно убывающую геометрическую прогрессию. Как известно, сумма первых n членов геометрической прогрессии вычисляется по формуле: S_n= . Мы только что доказали, что =0. Значит = . Получаем формулу суммы бесконечно убывающей геометрической прогрессии:

S= .

3) Примем без доказательства следующее утверждение:

= е.

Это равенство называют вторым замечательным пределом. Напомним, что число е – основание натурального логарифма – это иррациональное число, приближенно равное 2,71. 

Определение 3. Последовательность (а_n) называется бесконечно большой, если последовательность –бесконечно малая. Это записывают так: = .

Пример. Выше мы видели, что =0, то есть последовательность – бесконечно малая. Значит, последовательность – бесконечно большая: = .