2. Обзор элементарных функций

2.1. Простейшие функции

1. Линейной функцией называют функцию вида y=kx+b, где k и b – любые действительные числа. Область определения этой функции – все множество действительных чисел: D(y)=R. Область значений Е(y) зависит от коэффициента k: если k0, то E(y)=R; если k=0, то E(y)={b}.

На чертежах показаны графики линейной функции: для k>0, для k=0, для k<0. Из графиков видно, что при k>0 функция возрастает, при k=0 функция постоянна, при k<0 функция убывает. Для построения графика линейной функции достаточно найти две точки графика и соединить их прямой линией.

2. Квадратичной функцией называют функцию вида y=ax²+bx+c, где a, b и c – действительные числа, а0. Область определения этой функции – все множество действительных чисел: D(y)=R. Область значений Е(y) зависит от коэффициента а: если а>0, то E(y)= ; если a<0, то E(y)= .

На чертежах показаны графики квадратичной функции: для a<0, для a>0. При a<0 функция возрастает на промежутке и убывает на промежутке ; при a>0 функция убывает на промежутке и возрастает на промежутке . Для построения графика квадратичной функции достаточно найти вершину параболы (точку с абсциссой х_о= ), провести ось симметрии параболы (прямую х= ) и построить еще две пары точек графика, симметричных относительно этой оси; затем через полученные точки проводят параболу.

3. Дробно-линейной функцией называют функцию вида y= , где a, b и c – действительные числа, с0,

ad–bc0. Область определения этой функции

D(y)=(–;– )(– ;), а область значений

Е(y)=(–; )( ;) . График функции – гипербола с асимптотами х = – и у = . Возможны два расположения гиперболы относительно асимптот, показанные на чертеже.

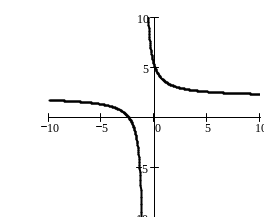
Для построения графика дробно-линейной функции достаточно построить асимптоты гиперболы: х= – и у= , – а затем найти какую-нибудь точку на графике (например, точку с абсциссой 0 или 1). Этим определяется положение ветвей гиперболы относительно асимптот; ветви проводятся симметрично относительно точки (– ; ).

2.2. Степенные функции

Степенной функцией называют функцию вида y=x^, где  – действительное число, 0, 1. Рассмотрим степенную функцию при различных .

1. Если =nN, n1, то D(y)=R. Если n четно, то E(y)=[0;); если n нечетно, то E(y)= R. На чертежах показаны графики степенной функции с натуральным показателем: для n четного, для n нечетного. Из графиков видно, что при четном n функция убывает на промежутке (–;0] и возрастает на промежутке [0;); при нечетном n функция возрастает.

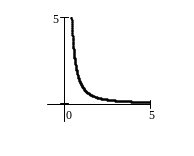
2. Если = –n, где nN, то D(y)=(–;0)(0;). Если n четно, то E(y)= (0;); если n нечетно, то E(y)= (–;0)(0;).

На чертежах показаны графики степенной функции с отрицательным целым показателем –n: для n четного, для n нечетного. Из графиков видно, что при четном n функция возрастает на промежутке (–;0) и убывает на промежутке (0;); при нечетном n функция убывает на промежутке

(–;0) и убывает на промежутке (0;).

3. Если = – несократимая дробь, где nN, n1, mZ, m0, то D(y)=[0;), если m>0, и D(y)=(0;), если m<0.

На чертежах показаны графики степенной функции с дробным показателем : для <0, для 0< <1, для >1. Из графиков видно, что в первом случае функция убывает, во втором и в третьем случае – возрастает.

4. Если  – иррациональное число, то D(y)=[0;), если >0, и D(y)=(0;), если <0. На чертежах показаны графики степенной функции с иррациональным показателем : для <0, для 0<<1, для >1. Из графиков видно, что в первом случае функция убывает, во втором и в третьем случае – возрастает.