
- •Часть 1
- •Раздел I. Элементы аналитической геометрии
- •1. Векторы на плоскости и в пространстве
- •1.1. Основные понятия
- •1.2. Линейные операции над векторами
- •1.3. Проекция вектора на ось
- •1.4. Базисы плоскости и пространства
- •1.5. Прямоугольная декартова система координат
- •1.6. Координаты вектора в прямоугольной декартовой
- •1.7. Скалярное произведение векторов
- •3. Скалярные квадраты базисных ортов равны 1, а их попарные скалярные произведения равны нулю.
- •1.8. Векторное произведение векторов
- •3. Попарные произведения базисных ортов вычисляются по формулам:
- •1.9. Смешанное произведение векторов
- •2. Линии на плоскости
- •2.1. Общее уравнение прямой на плоскости
- •2.2. Различные виды уравнения прямой на плоскости
- •2.3. Взаимное расположение двух прямых на плоскости
- •2.4. Расстояние от точки до прямой на плоскости
- •2.5. Эллипс, гипербола, парабола
- •2.6. Преобразование координат на плоскости
- •2.7. Общее уравнение кривой второго порядка
- •4О. (или ) – гипербола.
- •2.8. Полярные координаты на плоскости
- •3. Линии и поверхности в пространстве
- •3.1. Уравнение плоскости
- •3.2. Угол между плоскостями.
- •3.3. Уравнения прямой в пространстве
- •3.4. Угол между прямыми в пространстве.
- •3.5. Взаимное расположение двух прямых
- •3.6. Поверхности второго порядка
- •Раздел II. Введение в анализ
- •1. Комплексные числа
- •1.2. Тригонометрическая форма комплексного числа
- •2. Обзор элементарных функций
- •2.1. Простейшие функции
- •2.2. Степенные функции
- •2.3. Показательные и логарифмические функции
- •2.4. Тригонометрические функции
- •2.4. Обратные тригонометрические функции
- •3. Пределы
- •3.1. Предел числовой последовательности
- •3.3. Предел функции в точке
- •3.4. Непрерывность функции
- •Часть 1
- •127994, Москва, ул. Образцова, 15
3.3. Уравнения прямой в пространстве
1о. Поскольку прямая в пространстве – это линия пересечения двух плоскостей, то общее уравнение прямой в пространстве имеет вид:
![]() ,
,
где
![]() и
и
![]() .
.
2о. Уравнение прямой, проходящей через две различные точки А и В:
![]() .
.
Это уравнение получается из коллинеарности векторов и , где точка М(х;у;z) принадлежит прямой.
3о. Каноническое уравнение прямой, проходящей через точку Мо(хо;уо;zo) и имеющей направляющий вектор =(ах;ау;az):
![]() .
.
Это уравнение вытекает из коллинеарности векторов и , где точка М(х;у;z) принадлежит прямой.
4о. Параметрическое уравнение прямой, проходящей через точку Мо(хо;уо;zo) и имеющей направляющий вектор =(ах;ау;az):
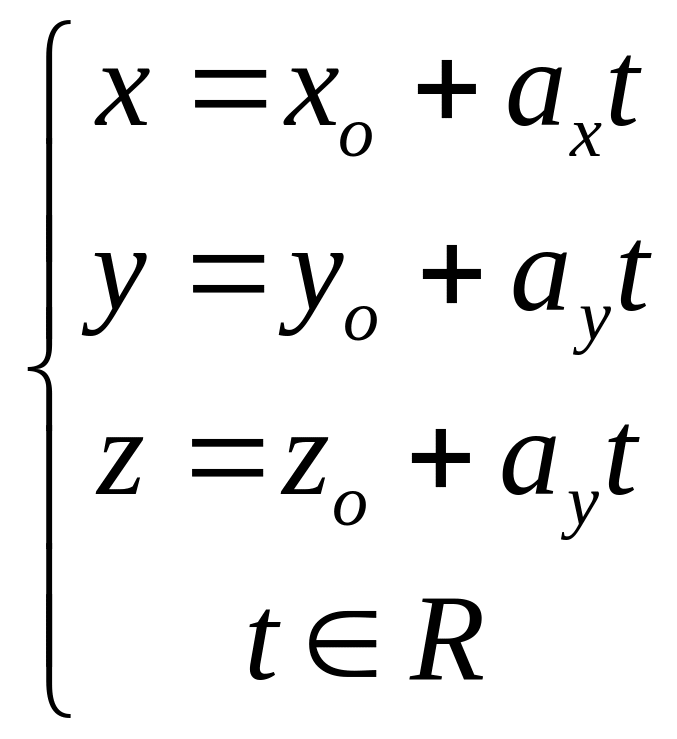 .
.
Это уравнение получается из канонического уравнения, если обозначить через t каждую из равных дробей.
Пример. Составим
каноническое и параметрическое уравнения
прямой, имеющей общее уравнение
![]() .
Для этого нужно найти точку Мо(хо;уо;zo),
лежащую на прямой, и ее направляющий
вектор
=(ах;ау;az).
Подберем значения хо, уо
и zо так, чтобы
они удовлетворяли системе уравнений.
Пусть, например, zо=0.
Подставим это значение в систему и решим
ее относительно хо и уо:
.
Для этого нужно найти точку Мо(хо;уо;zo),
лежащую на прямой, и ее направляющий
вектор
=(ах;ау;az).
Подберем значения хо, уо
и zо так, чтобы
они удовлетворяли системе уравнений.
Пусть, например, zо=0.
Подставим это значение в систему и решим
ее относительно хо и уо:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Итак, точка с координатами (–5;3;0)
принадлежит прямой.
.
Итак, точка с координатами (–5;3;0)
принадлежит прямой.
Далее, поскольку
данные плоскости имеют нормальные
векторы
![]() =(3;2;–7)
и
=(3;2;–7)
и
![]() =(4;–1;12)
соответственно, то направляющей вектор
прямой перпендикулярен обоим векторам
и
.
Поэтому в качестве направляющего вектора
можно взять векторное произведение
и
.
Имеем:
=(4;–1;12)
соответственно, то направляющей вектор
прямой перпендикулярен обоим векторам
и
.
Поэтому в качестве направляющего вектора
можно взять векторное произведение
и
.
Имеем:
=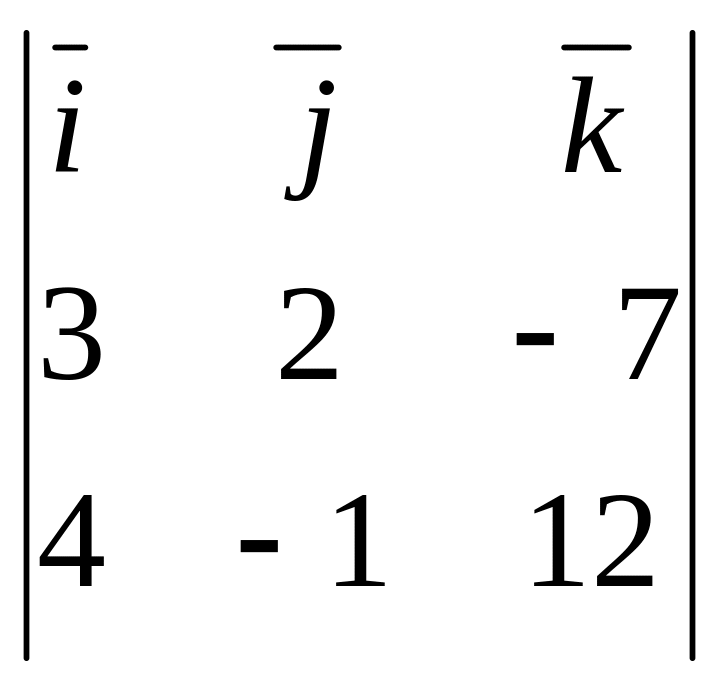 =
=
![]() –
–![]() +
+![]()
=17
–64
–11![]() .
Значит, направляющий вектор прямой
имеет координаты (17;–64;–11).
.
Значит, направляющий вектор прямой
имеет координаты (17;–64;–11).
Каноническое
уравнение:
![]() ;
;
параметрическое
уравнение:
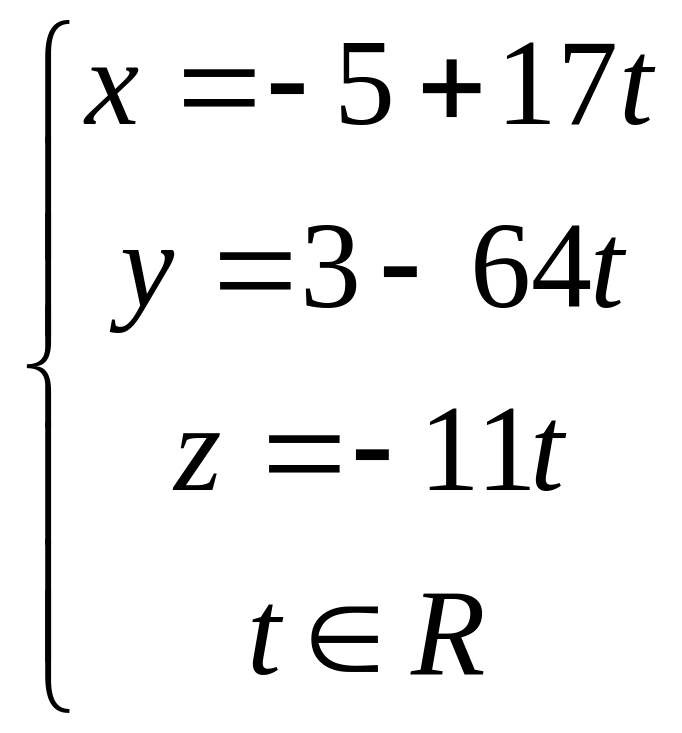 .
.
3.4. Угол между прямыми в пространстве.
Угол между прямой и плоскостью
Так
же, как и на плоскости, косинус угла
между прямыми в пространстве равен
модулю косинуса угла между их направляющими
векторами. Поэтому косинус угла между
прямыми, имеющими направляющие векторы
=(ах;ау;az)
и
![]() =(bх;bу;bz),
вычисляется по формуле:
=(bх;bу;bz),
вычисляется по формуле:
cos
=
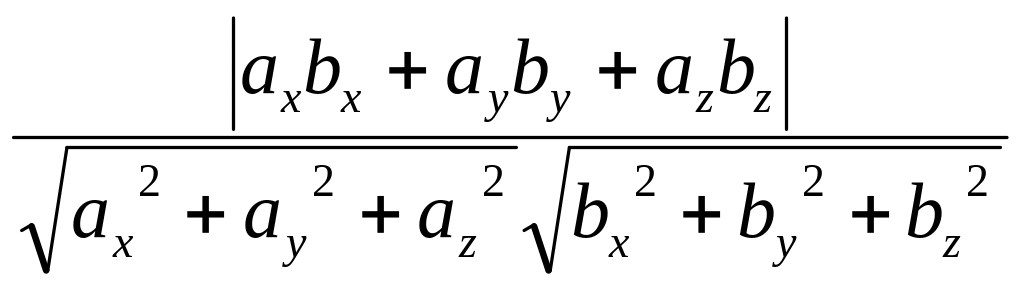 .
.
Из этой формулы получаем условие перпендикулярности двух прямых: прямые, имеющие направляющие векторы =(ах;ау;az) и =(bх;bу;bz), перпендикулярны тогда и только тогда, когда
aхbx + ayby + azbz = 0.
Рассмотрим теперь угол между прямой и плоскостью. Если прямая лежит в плоскости или параллельна ей, то угол между прямой и плоскостью считается равным нулю. Если прямая пересекает плоскость, то угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость. А этот угол, в свою очередь, равен либо 90о–, либо –90о, где – угол между направляющим вектором прямой и нормальным вектором плоскости. Поэтому
sin=cos. Если нормальный вектор плоскости =(А;В;С) и направляющий вектор прямой =(ах;ау;az), то получаем формулу синуса угла между прямой и плоскостью:
sin
=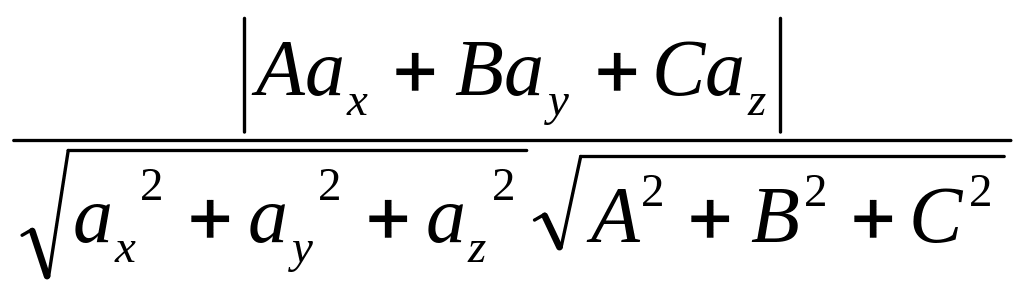 .
.
3.5. Взаимное расположение двух прямых
в пространстве
Две
прямые в пространстве либо совпадают,
либо параллельны, либо пересекаются,
либо скрещиваются (не лежат в одной
плоскости). Пусть первая прямая проходит
через точку М1(х1;у1;z1)
с направляющим вектором
![]() ,
а вторая – через точку М2(х2;у2;z2)
с направляющим вектором
,
а вторая – через точку М2(х2;у2;z2)
с направляющим вектором
![]() .
.
1) Если векторы , и коллинеарны, то прямые совпадают.
2) Если векторы и коллинеарны, но не коллинеарны вектору , то прямые параллельны.
3) Если векторы и не коллинеарны, но компланарны вектору , то прямые пересекаются.
4) Если векторы , и не компланарны, то прямые скрещиваются.
Примеры. Определим взаимное расположение прямых, проходящих через данные точки с данными направляющими векторами.
1) Пусть
=
(1;2;3), М1(0;1;–2),
=
(4;5;6), М2(7;9;7). Направляющие
векторы не коллинеарны:
![]() – значит, прямые либо пересекаются,
либо скрещиваются. Для уточнения
определим, компланарны ли векторы
,
и
:
.
.
=
– значит, прямые либо пересекаются,
либо скрещиваются. Для уточнения
определим, компланарны ли векторы
,
и
:
.
.
=
 =
= =
0. Значит, векторы компланарны. Ответ:
прямые пересекаются.
=
0. Значит, векторы компланарны. Ответ:
прямые пересекаются.
2) Пусть
=
(2;–1;3), М1(1;2;3),
=
(–4;2;–6), М2(5;1;9). Направляющие
векторы коллинеарны:
![]() – значит, прямые либо совпадают, либо
параллельны. Для уточнения определим,
коллинеарны ли векторы
и
:
=(4;–1;6),
– значит, прямые либо совпадают, либо
параллельны. Для уточнения определим,
коллинеарны ли векторы
и
:
=(4;–1;6),
![]() .
Значит, эти векторы не коллинеарны.
Ответ: прямые параллельны.
.
Значит, эти векторы не коллинеарны.
Ответ: прямые параллельны.
3) Пусть
=
(2;–1;3), М1(1;2;3),
=
(–4;2;–6), М2(5;0;9). Направляющие
векторы коллинеарны:
– значит, прямые либо совпадают, либо
параллельны. Для уточнения определим,
коллинеарны ли векторы
и
:
=(4;–2;6),
![]() .
Значит, эти векторы коллинеарны. Ответ:
прямые совпадают.
.
Значит, эти векторы коллинеарны. Ответ:
прямые совпадают.
4) Пусть
=
(1;2;3), М1(0;1;–2),
=
(4;5;6), М2(0;1;1). Направляющие
векторы не коллинеарны:
– значит, прямые либо пересекаются,
либо скрещиваются. Для уточнения
определим, компланарны ли векторы
,
и
:
.
.
=
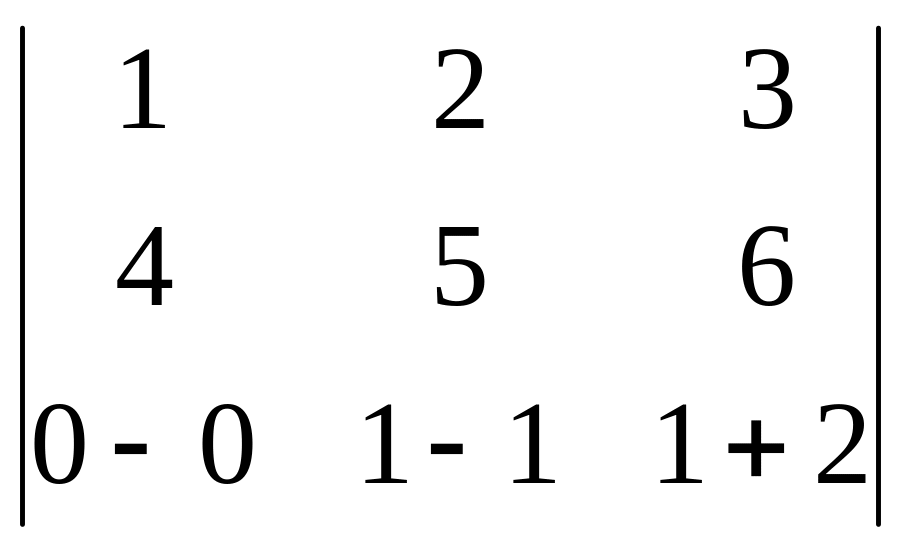 =
= =
–9 0. Значит, векторы
не компланарны. Ответ: прямые скрещиваются.
=
–9 0. Значит, векторы
не компланарны. Ответ: прямые скрещиваются.
