7 Циркуляція вектора напруженості магнітного поля. Закон повного струму.

Криволінійний інтеграл виду 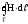називається циркуляцією вектора, в даному випадку напруженості магнітного поля. Знайдемо його значення на прикладі магнітного поля, створеного прямолінійним нескінченним провідником із струмом І. Виберемо довільний замкнутий контур ℓ, який охоплює провідник (рис.9.12).

В загальному випадку . (9.23)

Циркуляція вектора напруженості магнітного поля дорівнює алгебраїчній сумі струмів, які охоплює цей контур. Це співвідношення називають ще законом повного струму. В (9.23) струми, напрямок яких співпадає з поступальним рухом правого гвинта, який обертається в напрямку обходу контуру, беруться із знаком (+), а протилежні - із знаком (-). Слід зауважити, що на форму контуру ℓ ніяких обмежень не було, тобто він може бути довільним.

Той факт, що циркуляція вектора напруженості магнітного поля відмінна від нуля , свідчить про не потенціальний, а вихровий характер поля.

Приклад. Застосуємо цей закон для розрахунку магнітного поля прямолінійного нескінченного провідника із струмом

Так як форма контуру не має значення, виберемо його у формі кола, вісь якого співпадає із провідником (рис.9.13). Це дає право вважати, що величина вектора напруженості у всіх точках контуру однакова, а кут між вектором напруженості і вектором дорівнює 0^о. Тому маємо . Звідси одержуємо відому формулу (9.13) .

8. Напруженість магнітного поля довгого соленоїда

Виберемо контур ℓ у формі прямокутника. Будемо нехтувати крайовими ефектами, тобто будемо вважати, що магнітне поле зосереджене всередині котушки, а за її межами напруженість дорівнює нулю. Застосуємо закон повного струму

Сума струмів дорівнює . Тоді .

Отже напруженість магнітного поля в середині довгого соленоїда

,

а індукція відповідно

.

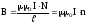9. Магнітний потік.

В теорії магнетизму, так же, як і в електростатиці, вводиться поняття потоку вектора індукції

. (9.25)

В_n – проекція вектора індукції на перпендикуляр до площадки.

(вебер).

На відміну від потоку вектора електростатичної індукції через замкнуту площу, який, як відомо (7.14) дорівнює алгебраїчній сумі зарядів, потік вектора індукції магнітного поля через довільну замкнуту поверхню дорівнює нулю

. (9.26)

Це є теорема Остроградського Гауса для магнітного поля. Рівність нулю означає, що в природі не існує уособлених джерел північного, або південного полюсів магніту.

10 Механічна робота в магнітному полі

Знайдемо роботу dA по переміщенню елементу провідника dℓ із струмом І у магнітному полі індукцією В. Сила Ампера переміщує провідник на відстань dx. Враховуючи (9.1) і (9.25), знайдемо роботу

, або , (9.29)

одержали, що робота по переміщенню провідника із струмом у магнітному полі дорівнює добуткові струму на магнітний потік через площу, яку описує провідник при своєму рухові.