
- •Спеціальна теорія відносності (релятивістська механіка)
- •1 Принцип відносності Галілея. Правило додавання швидкостей в класичній механіці
- •2.Парадокс Майкельсона і Морлі (1881-1887р.)
- •3.Постулати Ейнштейна. Відносність одночасності.
- •Перетворення Лоренца. Додавання швидкостей в релятивістській механіці.
- •5.Відносність часу. Відносність довжини тіл в напрямі руху. Просторово-часове співвідношення.
- •6.Залежність маси тіл від швидкості
- •7.Закони релятивістської динаміки
- •8. Зв’язок маси і енергії. Енергія зв’язку. Дефект мас
- •9.Зв’язок енергії та імпульсу
Спеціальна теорія відносності (релятивістська механіка)
-
Принцип відносності Галілея. Правило додавання швидкостей в класичній механіці.
-
Парадокс Майкельсона і Морлі (1881-1887р.)
-
Постулати Ейнштейна. Відносність одночасності.
-
Перетворення Лоренца. Додавання швидкостей в релятивістській механіці.
-
Відносність часу. Відносність довжини тіл в напрямі руху. Просторово-часове співвідношення.
-
Залежність маси тіл від швидкості.
-
Закони релятивістської динаміки.
-
Зв’язок маси і енергії. Енергія зв’язку. Дефект мас.
-
Зв’язок енергії та імпульсу.
1 Принцип відносності Галілея. Правило додавання швидкостей в класичній механіці
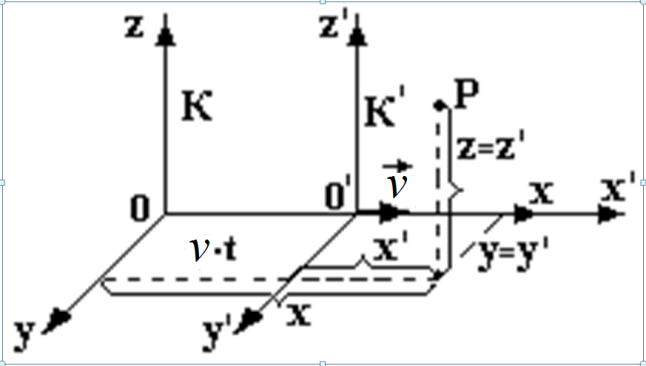
Рис. 1.
Розглянемо
інерціальну систему К(x,y,z) і систему
К1(x1,y1,z1),
яка рухається відносно системи К з
постійною швидкістю
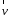 вздовж осі х. Для простоти будемо
вважати, що осі y
і z
паралельні осям y1
і z1
відповідно. Нехай початки
координат 0 і 01
в початковий момент часу співпадають.
Тоді запишемо очевидні
співвідношення
між координатами в якийсь момент часу
t
= t1:
вздовж осі х. Для простоти будемо
вважати, що осі y
і z
паралельні осям y1
і z1
відповідно. Нехай початки
координат 0 і 01
в початковий момент часу співпадають.
Тоді запишемо очевидні
співвідношення
між координатами в якийсь момент часу
t
= t1:
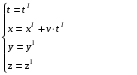
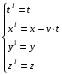 . (1.1)
. (1.1)
Рівняння (1.1) називаються перетвореннями координат Галілея.
Розглянемо наслідки цих перетворень.
-
Візьмемо перші похідні за часом
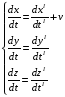

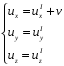 ,
або
,
або
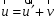 (1.2)
(1.2)
Одержали
правило складання швидкостей в класичній
механіці: абсолютна швидкість
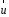 дорівнює векторній сумі відносної
дорівнює векторній сумі відносної
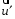 і переносної
і переносної
 швидкостей.
швидкостей.
Наприклад,
човен пливе по річці. Швидкість течії
ріки відносно
берега
– це переносна швидкість (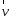 ),
швидкість човна відносно води – відносна
(
),
швидкість човна відносно води – відносна
(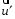 ),
результуюча швидкість човна відносно
берега – абсолютна (
),
результуюча швидкість човна відносно
берега – абсолютна ( ).
).
2. Візьмемо ще раз з рівняння (1.2) похідні за часом
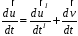 .
.
Так
як
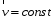 ,
то
,
то
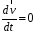 ,
,
або
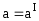 .
(1.3)
.
(1.3)
У всіх інерціальних системах прискорення тіла однакове. Це значить, що: «Другий закон Ньютона інваріантний (незмінний) в усіх інерціальних системах відліку».
Принцип відносності Галілея:
В замкнутій інерціальній системі відліку ніякими механічними дослідами неможливо встановити рухається вона чи знаходиться у стані спокою відносно інших інерціальних систем відліку.
Іншими словами: У всіх інерціальних системах відліку одні і ті ж механічні явища протікають однаково.
2.Парадокс Майкельсона і Морлі (1881-1887р.)


Рис. 2.



3.Постулати Ейнштейна. Відносність одночасності.


Таким чином:
ПОСТУЛАТ 1 (Принцип відносності Ейнштейна).
Фізичні закони однакові в усіх інерціальних системах відліку. Немає абсолютних систем відліку; всі системи відліку відносні і рівноправні.
ПОСТУЛАT 2 (Принцип сталої швидкості світла)
Швидкість світла у вакуумі не залежить від руху джерела і однакова в усix інерціальних системах відліку.
-
Перетворення Лоренца. Додавання швидкостей в релятивістській механіці.
У випадку великих швидкостей виявилися придатними перетворення координат і часу, запропоновані Лоренцом.
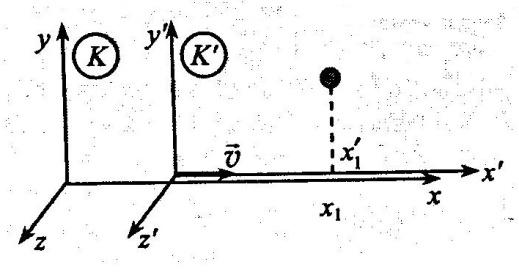
Рис. 6.
Нехай
інерціальна система
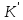 рухасться зі сталою швидкістю v
відносно інерціальної системи К вздовж
суміщених осей x
i
х
рухасться зі сталою швидкістю v
відносно інерціальної системи К вздовж
суміщених осей x
i
х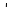 Тоді
перетворення
Лоренца
мають вигляд:
Тоді
перетворення
Лоренца
мають вигляд:


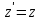

Проаналізуємо перетворення Лоренца.
1.При
швидкостях руху тіла, набагато менших
від швидкості світла, перетворення
Лоренца мають переходити в перетворення
Галілея. Справді, якщо
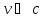 ,
то
,
то
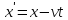
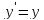

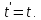
2.Перетворення
Лоренца потребують змін
правил додавання
швидкостей.
Дістанемо ці нові правила.
Нехай
матеріальна точка рухається
зі швидкістю u
відносно системи К.
Знайдемо її швидкість
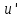 відcносно
системи
відcносно
системи
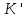 .
У
класичній механіці правило додавання
швидкостей таке:
.
У
класичній механіці правило додавання
швидкостей таке:
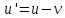 . Воно знайдене диференціюванням
перетворень координат Галілея. З
перетворень Лоренца також випливає
релятивістське правило додавання
швидкостей:
. Воно знайдене диференціюванням
перетворень координат Галілея. З
перетворень Лоренца також випливає
релятивістське правило додавання
швидкостей:
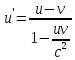
Проаналізуємо здобуту формулу.
1.Формула
переходить у класичну коли
v
 c,
u
c,
u
 c:
c:
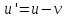 .
.
2. Ні при яких значеннях швидкостей, відносна швидкість тіл не може перевищити швидкості світла. Справді, нехай швидкості u і v напрямлені назустріч одна одній. Тоді слід і в чисельникy і знаменнику поставити знак «плюс» .
Візьмемо
граничний випадок u
= c
та v
= с,
тобто матеріальна точка
рухається
відносно системи К
зi
швидкістю світла, а спостерігач рухається
разом із системою
 їй
назустріч також із швидкістю світла.
І що ж він бачить ?:
їй
назустріч також із швидкістю світла.
І що ж він бачить ?:
 .
.
Він бачить, що точка рухaється назустріч йому тільки зі швидкістю світла, а не з подвійною швидкістю світла, як це випливало з класичної формули додавання швидкостей. Pелятивістське правило додавання швидкостей стверджує існування граничної швидкості.
