
Контрольные задания
-
Доказать, что произведение
 гомеоморфно
гомеоморфно
 .
.
1.2 Доказать, что если
 замкнуто в
замкнуто в
 а
а
 замкнуто в
замкнуто в
 ,
то
,
то
 замкнуто
в
замкнуто
в
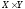 .
.
1.3 Доказать, что
 при любых
при любых
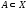 и
и
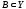 .
.
1.4 Доказать, что
 .
.
1.5
Доказать, что отображения
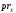 и
и
 непрерывны.
непрерывны.
1.6 Доказать, что для любых
отображений
 и
и
 существует одно и только одно отображение
существует одно и только одно отображение
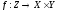 c
c
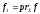 и
и
 .
.
1.7
Пусть
 и
и
 - базы топологий пространств
- базы топологий пространств
 и
и
 .
Показать, что множества
.
Показать, что множества
 с
с
 и
и
 составляют
базу пространства
составляют
базу пространства
 .
.
1.8
Доказать, что пространство
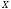 хаусдорфово тогда и только тогда, когда
множество
хаусдорфово тогда и только тогда, когда
множество
 замкнуто в
замкнуто в
 .
.
1.9 Доказать,
что если множество
 открыто
в
открыто
в
 ,
то множество
,
то множество
 открыто в
открыто в
 .
.
1.10 Построить для точек
 и
и
 две непересекающиеся окрестности в
топологическом пространстве
две непересекающиеся окрестности в
топологическом пространстве
 ,
где
,
где
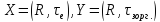 .
.
1.11 Пусть
 и
и
 – топологические пространства,
– топологические пространства,
 .
Показать, что топология, индуцированная
на
.
Показать, что топология, индуцированная
на
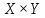 ,
совпадает с топологией произведения
подпространств
,
совпадает с топологией произведения
подпространств
 и
и
 .
.
1.12 Показать, что топология произведения топологических пространств с дискретной топологией дискретна.
1.13 Пусть
 и
и
 – топологические пространства. Показать,
что срез открытого множества произведения
– топологические пространства. Показать,
что срез открытого множества произведения
 является открытым множеством.
является открытым множеством.
1.14 Показать, что топология произведения топологических пространств с антидискретной топологией антидискретна.
1.15 Пусть
 и
и
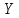 – топологические пространства. Показать,
что срез замкнутого множества произведения
– топологические пространства. Показать,
что срез замкнутого множества произведения
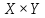 является замкнутым множеством.
является замкнутым множеством.
1.16 Показать, что произведение компактных пространств компактно.
1.17 Доказать, что проекции произведения
 топологических пространств
топологических пространств
 и
и
 – открытые множества.
– открытые множества.
1.18 Пусть
 и
и
 – топологические пространства и
– топологические пространства и
 .
Доказать, что множество подмножеств
произведения
.
Доказать, что множество подмножеств
произведения
 вида
вида
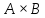 ,
где
,
где
 – окрестность точки
– окрестность точки
 и
и
 - окрестность точки
- окрестность точки
 ,
является фундаментальной системой
окрестностей точки
,
является фундаментальной системой
окрестностей точки
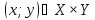 .
.
1.19 Построить для точки
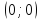 две различные окрестности в топологическом
пространстве
две различные окрестности в топологическом
пространстве
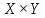 ,
где
,
где
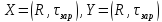 .
.
1.20 Показать, что если топологические
пространства
 и
и
 удовлетворяют первой аксиоме счетности,
то и
удовлетворяют первой аксиоме счетности,
то и
 так же удовлетворяет первой аксиоме
счетности.
так же удовлетворяет первой аксиоме
счетности.
1.21 Показать, что если топологические
пространства
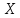 и
и
 удовлетворяют аксиоме отделимости
удовлетворяют аксиоме отделимости
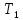 ,
то и
,
то и
 так же удовлетворяет аксиоме отделимости
так же удовлетворяет аксиоме отделимости

1.22 Показать, что если топологические
пространства
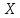 и
и
 удовлетворяют второй аксиоме счетности,
то и
удовлетворяют второй аксиоме счетности,
то и
 так же удовлетворяет второй аксиоме
счетности.
так же удовлетворяет второй аксиоме
счетности.
1.23 Показать, что если топологические
пространства
 и
и
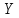 удовлетворяют аксиоме отделимости
удовлетворяют аксиоме отделимости
 ,
то и
,
то и
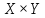 так же удовлетворяет аксиоме отделимости
так же удовлетворяет аксиоме отделимости
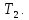
1.24 Показать, что если топологические
пространства
 и
и
 является связным, то и
является связным, то и
 так же является связным пространством.
так же является связным пространством.
1.25 Показать, что если топологические
пространства
 и
и
 удовлетворяют аксиоме отделимости
удовлетворяют аксиоме отделимости
 ,
то и
,
то и
 так же удовлетворяет аксиоме отделимости
так же удовлетворяет аксиоме отделимости

1.26 Построить для точки
 две различные окрестности в топологическом
пространстве
две различные окрестности в топологическом
пространстве
 ,
где
,
где
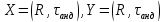
1.27 Найти внутренность, замыкание
и границу отрезка
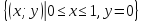 в
топологическом пространстве
в
топологическом пространстве
 , где
, где
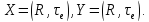
1.28 Найти внутренность, замыкание и
границу множества
 в топологическом пространстве
в топологическом пространстве
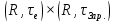
1.29 Пусть
 .
Построить какое либо топологическое
пространство
.
Построить какое либо топологическое
пространство
 .
.
1.30 Найти внутренность, замыкание
и границу множества
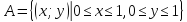 в
топологическом пространстве
в
топологическом пространстве
 , где
, где

2.1
Пусть
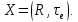 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 .
Дать описание топологии на
.
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.2
Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 .
Дать описание топологии на
.
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.3
Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на
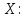
 Дать описание топологии на
Дать описание топологии на
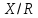 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.4
Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на


 Дать описание топологии на
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.5
Пусть
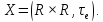 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на
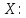
 .
Дать описание топологии на
.
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.6 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на
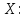
 .
Дать описание топологии на
.
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.7
Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

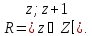 Дать описание топологии на
Дать описание топологии на
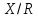 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.8
Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

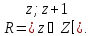 Дать описание топологии на
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.9
Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на


 Дать описание топологии на
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.10 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

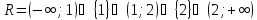 .
Дать описание топологии на
.
Дать описание топологии на
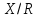 (указать открытые и замкнутые множества
в ней.
(указать открытые и замкнутые множества
в ней.
2.11 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 .
Найти границу множества
.
Найти границу множества
 в топологическом фактор пространстве
в топологическом фактор пространстве
 .
.
2.12
Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 .
Дать описание топологии на
.
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.13 Пусть
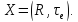 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 Дать описание топологии на
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.14 Показать,
что топологическое фактор пространство
с антидискретной топологией на
 является так же антидискретным.
является так же антидискретным.
2.15 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на


 Дать описание топологии на
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.16 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 .
Дать описание топологии на
.
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней.
(указать открытые и замкнутые множества
в ней.
2.17
Показать, что топологическое фактор
пространство с дискретной топологией
на
 является так же дискретным. .
является так же дискретным. .
2.18 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 Дать описание топологии на
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.19 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 .
Дать описание топологии на
.
Дать описание топологии на
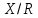 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.20 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на


 Дать описание топологии на
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.21 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 Дать описание топологии на
Дать описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.22 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на
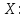
 Дать
описание топологии на
Дать
описание топологии на
 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.23 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на


 Найти внутренность, замыкание и
границу множества
Найти внутренность, замыкание и
границу множества

2.24
Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на
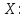

 Найти внутренность, замыкание и
границу множества
Найти внутренность, замыкание и
границу множества
 2.25 Пусть
2.25 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 .
Найти внутренность, замыкание и границу
множества
.
Найти внутренность, замыкание и границу
множества

 в
топологическом фактор пространстве
в
топологическом фактор пространстве

2.26 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на



Построить всевозможные окрестности
точки
 в топологическом фактор пространстве
в топологическом фактор пространстве

2.27 Пусть
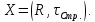 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 Построить окрестности точки
Построить окрестности точки
 в
топологическом фактор пространстве
в
топологическом фактор пространстве

2.28 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на

 .
Дать описание топологии на
.
Дать описание топологии на
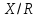 (указать открытые и замкнутые множества
в ней).
(указать открытые и замкнутые множества
в ней).
2.29 Пусть
 .
Построить какое либо нетривиальной
топологическое фактор пространство
.
Построить какое либо нетривиальной
топологическое фактор пространство
 .
.
2.30 Пусть
 Рассмотрим следующее отношение
эквивалентности на
Рассмотрим следующее отношение
эквивалентности на


 Найти внутренность, замыкание и
границу множества
Найти внутренность, замыкание и
границу множества

 в
топологическом фактор пространстве
в
топологическом фактор пространстве
 .
.
