
Примеры.
1.
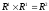 ,
,
 ,
,
 (где
(где
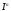 -
-
 -
мерный куб).
-
мерный куб).
2. 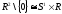 .
.
3. Пусть
 -
произвольное топологическое пространство,
-
произвольное топологическое пространство,
 ,
т.е. единственный
,
т.е. единственный
элемент
в
 - само пространство
- само пространство
 .
Ясно, что факторпространство
.
Ясно, что факторпространство
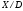 одноточечное, т.е.
одноточечное, т.е.
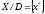 .
.
4. Пространство
 - произвольное,
- произвольное,
 ,
т.е. все элементы в
,
т.е. все элементы в
 одноточечные. Очевидно, что
одноточечные. Очевидно, что
 .
.
5. На
вещественной прямой
 зададим
разбиение
зададим
разбиение
 .
Будем считать, что
.
Будем считать, что
 ,
где
,
где
 - “большая точка” множества
- “большая точка” множества
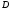 .
Множество
.
Множество
 можно изобразить на плоскости
можно изобразить на плоскости
 (т.
е. посредством биекции отождествить с
некоторым множеством на плоскости)
следующим образом. Первую четверть
разобьем на секторы:
(т.
е. посредством биекции отождествить с
некоторым множеством на плоскости)
следующим образом. Первую четверть
разобьем на секторы:
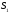 (от
(от
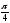 до
до
 ),
),
 (от
(от
 до
до
 ),
),
 (от
(от
 до
до
 )
и т.д., аналогично вторую
)
и т.д., аналогично вторую
четверть
на секторы:
 (от
(от
 до
до
 )
,
)
,
 (от
(от
 до
до
 )
и т.д. При склеивании
)
и т.д. При склеивании
множества
 в
точку
в
точку
 каждый
отрезок
каждый
отрезок
 ,
,
 ,
превращается в петлю. Обозначим её
,
превращается в петлю. Обозначим её
 для
для
 и
и
 для
для
 .
Каждую петлю
.
Каждую петлю
 поместим в секторе
поместим в секторе
 ,
располагая точку
,
располагая точку
 в начале координат. Тогда множество
в начале координат. Тогда множество
 можно представить себе в виде цветка
со счетным числом лепестков. Следует
однако отметить, что построенное
изображение не является топологическим
вложением. Его вообще не существует,
иначе говоря, топология в
можно представить себе в виде цветка
со счетным числом лепестков. Следует
однако отметить, что построенное
изображение не является топологическим
вложением. Его вообще не существует,
иначе говоря, топология в
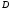 не индуцируется из плоскости. Точка
не индуцируется из плоскости. Точка
 не имеет в
не имеет в
 счетной локальной базы.
счетной локальной базы.
6. На плоскости
 рассмотрим замкнутый прямоугольник
рассмотрим замкнутый прямоугольник
 с естественной (т.е.
с естественной (т.е.
индуцированной из плоскости) топологией. Зафиксируем две его различные стороны
 и
зададим биекцию
и
зададим биекцию
 ,
заключающуюся в обычном наложении
отрезка
,
заключающуюся в обычном наложении
отрезка
 на отрезок
на отрезок
 с
предварительным (если это необходимо
) растяжением или сжатием. Всего таких
биекций две. Для однозначного задания
отображения
с
предварительным (если это необходимо
) растяжением или сжатием. Всего таких
биекций две. Для однозначного задания
отображения
 достаточно зафиксировать на каждом из
отрезков некоторое направление и
потребовать, чтобы при наложении эти
направления совмещались. Далее, рассмотрим
факторизацию прямоугольника, порожденную
разбиением
достаточно зафиксировать на каждом из
отрезков некоторое направление и
потребовать, чтобы при наложении эти
направления совмещались. Далее, рассмотрим
факторизацию прямоугольника, порожденную
разбиением
 и заключающуюся в склеивании каждой
точки
и заключающуюся в склеивании каждой
точки
 с соответствующей точкой
с соответствующей точкой
 .
Такая факторизация называется склеиванием
сторон
.
Такая факторизация называется склеиванием
сторон
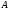 и
и
 .
.
Основные теоремы
Теорема
83. Отображения
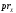 и
и
 непрерывны.
непрерывны.
Теорема 84. Слои произведения канонически гомеоморфны сомножителям. Каноническими гомеоморфизмами служат сужения проекций.
Теорема 85. Хаусдорфовость сохраняется при перемножении.
Теорема 86. Сепарабельность сохраняется при перемножении.
Теорема 87. Произведение пространств, удовлетворяющих первой аксиоме счетности,
удовлетворяет первой аксиоме счетности. То же верно и для второй аксиомы счетности.
Теорема 88. Метризуемость сохраняется при перемножении.
Теорема 89. Связность, а также линейная связность, сохраняются при перемножении.
Теорема 90. Компактность сохраняется при перемножении.
Теорема
91. Множество в факторпространстве
 открыто
тогда и только тогда, когда оно является
образом насыщенного открытого множества
при отображении
открыто
тогда и только тогда, когда оно является
образом насыщенного открытого множества
при отображении
 .
.
Теорема 92. Следующие утверждения эквивалентны:
1)
Множество
 в
факторпространстве
в
факторпространстве
 открыто;
открыто;
2) Прообраз множества
 при проекции замкнут в
при проекции замкнут в
 ;
;
3) Множество
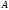 является образом насыщенного замкнутого
множества.
является образом насыщенного замкнутого
множества.
Теорема
93. Прекция
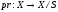 является
непрерывным отображением.
является
непрерывным отображением.
Теорема 94. Факторпространство линейно связного пространства линейно связно.
Теорема 95. Факторпространство сепарабельного пространства сепарабельно.
Теорема 96. Факторпространство компактного пространства компактно.
Теорема
97. Если
 -
топологические пространства,
-
топологические пространства,
 - разбиение пространства
- разбиение пространства
 на непустые множества и
на непустые множества и
 –
непрерывное отображение, постоянное
на каждом элементе разбиения
–
непрерывное отображение, постоянное
на каждом элементе разбиения
 ,
то фактор
,
то фактор
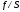 отображения
отображения
 является непрерывным отображением
(отображение
является непрерывным отображением
(отображение
 называется
инъективным фактором отображения).
называется
инъективным фактором отображения).
Теорема
98. Если
 непрерывное
отображение компактного пространства
непрерывное
отображение компактного пространства
 на Хаусдорфово пространство
на Хаусдорфово пространство
 ,
то инъективный фактор
,
то инъективный фактор
 является гомеоморфизмом.
является гомеоморфизмом.
Теорема 99. Инъективный фактор непрерывного отображения компактного пространства в хаусдорфово является топологическим вложением.
Теорема
100. (Транзитивность факторизации).
Если
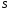 - разбиение пространства
- разбиение пространства
 и
и
 - разбиение пространства
- разбиение пространства
 ,
то факторпространтсво
,
то факторпространтсво
 канонически гомеоморфно
канонически гомеоморфно
 ,
где
,
где
 -
разбиение пространства
-
разбиение пространства
 на прообразы элементов разбиения
на прообразы элементов разбиения
 при
проекции
при
проекции
 .
.
