
Лабораторная работа 7. Произведение топологических пространств. Фактор – пространство. Основные понятия и определения.
Прямым произведением (декартовым
произведением или просто произведением)
множеств
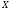 и
и
 называется множество
называется множество
 всех
упорядоченных пар
всех
упорядоченных пар
 с
с
 и
и
 .
Если
.
Если
 и
и
 ,
то
,
то
 .
Множества
.
Множества
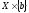 и
и
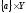 c
c
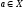 и
и
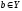 называются
слоями произведения
называются
слоями произведения
 .
.
Отображения произведения
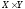 на
на
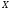 и
и
 ,
определяемые формулами
,
определяемые формулами
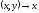 и
и
 обозначаются через
обозначаются через
 и
и
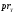 и называются проекциями.
и называются проекциями.
Пусть
 и
и
 –
топологические пространства. Множество
вида
–
топологические пространства. Множество
вида
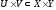 назовем
элементарным, если
назовем
элементарным, если
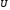 -
открыто в Х и V – открыто
в
-
открыто в Х и V – открыто
в
 .
.
Произведением пространств
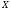 и
и
 называется
множество
называется
множество
 с топологией, базой которой служит
совокупность элементарных множеств.
с топологией, базой которой служит
совокупность элементарных множеств.
Всякому отображению
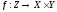 ,
где
,
где
 -
некоторые множества, соответствуют
(так называемые координатные)
отображения
-
некоторые множества, соответствуют
(так называемые координатные)
отображения
 и
и
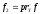 .
.
Если
имеются отображения
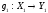 и
и
 ,
то возникает отображение
,
то возникает отображение
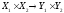 ,
определяемое формулой
,
определяемое формулой
 .
Это отображение называется произведением
отображений
.
Это отображение называется произведением
отображений
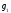 и
и
 и обозначается
и обозначается
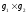 .
.
Будем говорить, что топологическое свойство сохраняется при перемножении, если из того, что сомножители обладают этим свойством, следует, что произведение тоже им обладает.
Пространство
 называется
тором.
называется
тором.
Произведение
 (
(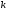 сомножителей) называется
сомножителей) называется
 -
мерным тором.
-
мерным тором.
Пусть
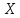 и
и
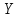 – топологические пространства,
– топологические пространства,
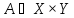 и
и
 .
Срезом подмножества
.
Срезом подмножества
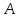 по элементу
по элементу
 называется множество таких точек
называется множество таких точек
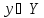 ,
что
,
что
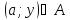 .
.
Пусть
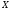 - некоторое множество,
- некоторое множество,
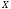 -
его разбиение (разбиением множества
называется его покрытие попарно
непересекающимися множествами).
Множество, элементами которого являются
подмножества множества
-
его разбиение (разбиением множества
называется его покрытие попарно
непересекающимися множествами).
Множество, элементами которого являются
подмножества множества
 ,
составляющие разбиение
,
составляющие разбиение
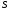 ,
называется фактормножеством
множества
,
называется фактормножеством
множества
 ,
по разбиению
,
по разбиению
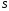 и обозначается через
и обозначается через
 (это множество называется также
фактормножеством множества
(это множество называется также
фактормножеством множества
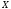 по соответствующему отношению
эквивалентности). Отображение
по соответствующему отношению
эквивалентности). Отображение
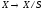 ,
относящее каждой точке
,
относящее каждой точке
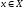 содержащий
ее элемент разбиения
содержащий
ее элемент разбиения
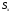 ,
называется проекцией или отображением
факторизации и обозначается через
,
называется проекцией или отображением
факторизации и обозначается через
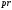 .
Подмножества множества
.
Подмножества множества
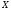 ,
составленные из целых элементов
разбиения, называются насыщенными.
Наименьшее насыщенное множество,
содержащее подмножество множества
,
составленные из целых элементов
разбиения, называются насыщенными.
Наименьшее насыщенное множество,
содержащее подмножество множества
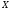 ,
называется его насыщением.
,
называется его насыщением.
Фактормножество
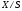 топологического пространства
топологического пространства
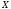 по любому разбиению
по любому разбиению
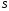 на непустые подмножества наделяется
естественной топологией: множество
на непустые подмножества наделяется
естественной топологией: множество
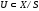 объявляется открытым в
объявляется открытым в
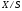 ,
если открыт его прообраз
,
если открыт его прообраз
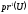 при отображении
при отображении
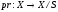 .
Совокупность таких множеств является
топологической структурой в
.
Совокупность таких множеств является
топологической структурой в
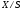 .
Эта топологическая структура называется
фактортопологией, а множество
.
Эта топологическая структура называется
фактортопологией, а множество
 ,
наделенное ею, называется факторпространством
пространства
,
наделенное ею, называется факторпространством
пространства
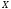 по разбиению
по разбиению
 .
.
Факторпространство квадрата
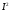 по
разбиению на одноточечные подмножества
его внутренности, четверку вершин, пары
точек оснований, расположенных на одной
вертикали, и пары точек боковых сторон,
симметричных относительно центра
называется бутылкой Клейна.
по
разбиению на одноточечные подмножества
его внутренности, четверку вершин, пары
точек оснований, расположенных на одной
вертикали, и пары точек боковых сторон,
симметричных относительно центра
называется бутылкой Клейна.
Факторпространство квадрата
 по разбиению на пары симметричных
относительно центра квадрата точек его
боковых сторон и на лежащие на боковых
сторонах одноточечные подмножества
гомеоморфно ленте Мебиуса, т.е.
поверхности, которая образуется в
по разбиению на пары симметричных
относительно центра квадрата точек его
боковых сторон и на лежащие на боковых
сторонах одноточечные подмножества
гомеоморфно ленте Мебиуса, т.е.
поверхности, которая образуется в
 отрезком,
поворачивающимся в полуплоскости на
отрезком,
поворачивающимся в полуплоскости на
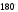 вокруг
своей середины при одновременном
вращении полуплоскости на
вокруг
своей середины при одновременном
вращении полуплоскости на
 вокруг
своей граничной прямой.
вокруг
своей граничной прямой.
