Упражнения.
-
Удовлетворяет ли второй аксиоме счетности топология стрелки на прямой?
-
Построить пример, показывающий, что сепарабельность не наследственна.
-
Построить метрическое пространство, не удовлетворяющее второй аксиоме
счетности.
-
Построить пример, показывающий, что непрерывный образ пространства,
удовлетворяющего второй аксиоме счетности, может не удовлетворять этой аксиоме.
-
Пусть пространство
удовлетворяет второй аксиоме счетности.
Доказать, что из
любой его базы можно выделить счетный набор множеств, также являющийся базой
пространства
.
-
Доказать, что в сепарабельном пространстве всякая совокупность попарно
непересекающихся открытых множеств счетна.
-
Доказать, что число компонент открытого множества
счетно. -
Доказать, что регулярное пространство со счетной базой нормально.
-
Построить пример топологического пространства без первой аксиомы счетности, (без второй аксиомы счетности).
10. Какие из следующих пространств Хаусдорфовы:
а) дискретное пространство;
б) антидискретное пространство;
в) стрелка.
-
Является ли отрезок
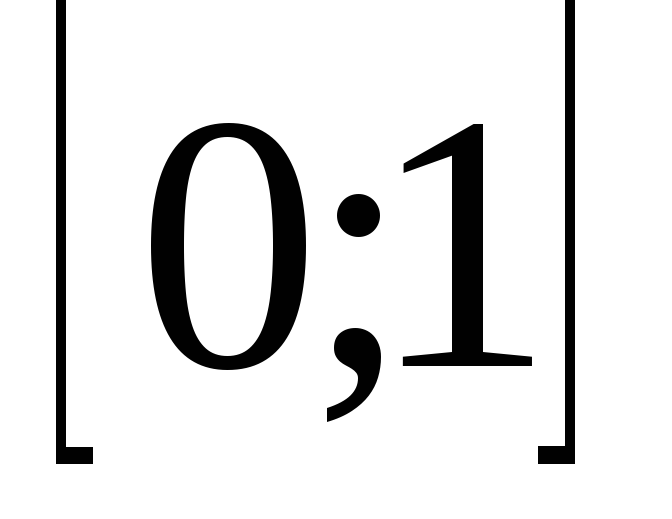с индуцированной из
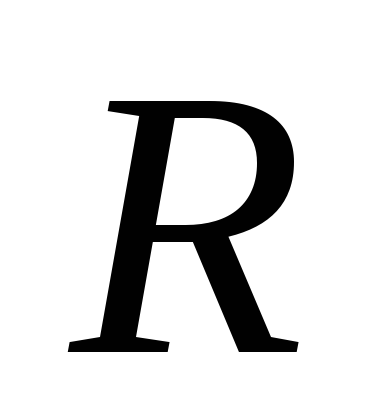топологией Хаусдорфовым?
Обладают ли в нем непересекающимися окрестностями точки 0 и 1? Какими?
-
Докажите, что множество совпадения двух непрерывных отображений произвольного пространства в Хаусдорфово пространство является замкнутым.
-
Докажите, что множество неподвижных точек непрерывного отображения Хаусдорфова пространства в себя является замкнутым.
14. Какие из следующих топологических свойств наследственны:
а) конечность множества точек;
б) бесконечность топологической структуры;
в) бесконечность множества точек;
г) связность;
д) линейная связность.
15. Докажите, что пространство удовлетворяет первой аксиоме отделимости тогда и
только тогда, когда любая его точка совпадает с пересечением ее окрестностей.
16. Являются ли замкнутым в Хаусдорфовом пространстве все конечные множества.
17. Приведите пример, показывающий, что из первой аксиомы отделимости вторая не
следует.
18. Докажите, что всякое метрическое пространство удовлетворяет первой аксиоме
отделимости.
19. Докажите, что в каждом множестве существует самая грубая топологическая
структура, удовлетворяющая первой аксиоме отделимости. Какова она?
20. Постройте нерегулярное Хаусдорфово пространство.
21. Постройте пространство, удовлетворяющее третьей аксиоме отделимости и не
удовлетворяющее второй.
22. Докажите, что пространство удовлетворяет третьей аксиоме отделимости тогда и
только тогда, когда в любой окрестности его точки содержится замыкание некоторой окрестности этой точки.
23. Постройте ненормальное регулярное пространство.
24. Постройте пространство, удовлетворяющее четвертой аксиоме отделимости и не
удовлетворяющее третьей.
25. Докажите, что пространство удовлетворяет четвертой аксиоме отделимости тогда и только тогда, когда в любой окрестности любого его замкнутого множества содержится замыкание некоторой окрестности этого множества.
26. Пусть
– непрерывное сюръективное отображение,
переводящее каждое
замкнутое
множество в замкнутое. Докажите, что
если
- нормально, то и
нормально.
-
Докажите, что в любом пространстве, которое не является Хаусдорфовым и
удовлетворяет первой аксиоме счетности, существует последовательность, сходящаяся одновременно к двум различным точкам.
28. Докажите, что, если пространство
нормально,
то нормальным является и любое
замкнутое
подпространство
.
-
Докажите, что любое регулярное пространство со счетной базой нормально.
-
Доказать, что метрическое топологическое пространство удовлетворяет аксиоме отделимости Хаусдорфа.