Определить параметры модели методом фиктивных переменных.
Построение модели с лаговыми переменными 3-его порядка. Общий вид модели:
Идентификация модели методом фиксированных переменных. Для определения коэффициентов переходим к переменным вида:
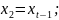
Замена переменных:
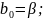
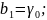
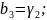
С учетом принятых обозначений модель будет иметь вид:
Оценка параметров модели производится классическим МНК, при условии выполнения всех его предположений. Для оценки независимых параметров запишем таблицу исходных данных с новыми переменными с учетом лага p=3.
t |
xt |
yt |
|
|
|
|
|
1 |
1,52 |
17,955 |
|
|
|
|
|
2 |
1,23 |
16,842 |
|
|
|
|
|
3 |
1,78 |
18,448 |
y |
x1 |
x2 |
x3 |
x4 |
4 |
1,45 |
18,286 |
18,286 |
1,45 |
1,78 |
1,23 |
1,52 |
5 |
1,48 |
17,388 |
17,388 |
1,48 |
1,45 |
1,78 |
1,23 |
6 |
1,12 |
16,345 |
16,345 |
1,12 |
1,48 |
1,45 |
1,78 |
7 |
1,34 |
15,029 |
15,029 |
1,34 |
1,12 |
1,48 |
1,45 |
8 |
1,38 |
15,626 |
15,626 |
1,38 |
1,34 |
1,12 |
1,48 |
9 |
1,45 |
16,241 |
16,241 |
1,45 |
1,38 |
1,34 |
1,12 |
10 |
1,14 |
16,1 |
16,1 |
1,14 |
1,45 |
1,38 |
1,34 |
11 |
1,58 |
17,446 |
17,446 |
1,58 |
1,14 |
1,45 |
1,38 |
12 |
1,45 |
17,351 |
17,351 |
1,45 |
1,58 |
1,14 |
1,45 |
13 |
1,24 |
16,872 |
16,872 |
1,24 |
1,45 |
1,58 |
1,14 |
14 |
1,35 |
16,087 |
16,087 |
1,35 |
1,24 |
1,45 |
1,58 |
15 |
1,68 |
17,496 |
17,496 |
1,68 |
1,35 |
1,24 |
1,45 |
16 |
1,65 |
18,844 |
18,844 |
1,65 |
1,68 |
1,35 |
1,24 |
17 |
1,56 |
18,904 |
18,904 |
1,56 |
1,65 |
1,68 |
1,35 |
18 |
1,5 |
19,214 |
19,214 |
1,5 |
1,56 |
1,65 |
1,68 |
В результате расчетов получим:
Получим:
Проведем проверку коэффициентов модели критерием Стьюдента.
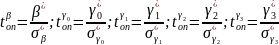
Так
как
,значит, коэффициенты γ0,
γ1,
γ2
являются
значимыми, коэффициенты β, γ3
не является значимым, следовательно,
можно его исключить. В результате
получим:
Проанализировать влияние лаговых переменных xt-p для всех p=1,..,n на результативную переменную yt. Сделать выводы.
Краткосрочный мультипликатор:
В
краткосрочном периоде при изменении
на одну единицу
изменится на 4,4588.
xt |
yt |
1,45 |
6,465309 |
1,48 |
6,599074 |
1,12 |
4,993894 |
1,34 |
5,974837 |
1,38 |
6,15319 |
1,45 |
6,465309 |
1,14 |
5,08307 |
1,58 |
7,044957 |
1,45 |
6,465309 |
1,24 |
5,528954 |
1,35 |
6,019425 |
1,68 |
7,490841 |
1,65 |
7,357076 |
1,56 |
6,955781 |
1,5 |
6,68825 |
Среднесрочный мультипликатор:
В
среднесрочном периоде при изменении
на одну единицу
изменится на 8,7528.
xt |
xt-1 |
yt |
1,45 |
1,78 |
14,10865677 |
1,48 |
1,45 |
12,8253966 |
1,12 |
1,48 |
11,34903695 |
1,34 |
1,12 |
10,7841347 |
1,38 |
1,34 |
11,9071715 |
1,45 |
1,38 |
12,39105049 |
1,14 |
1,45 |
11,30939315 |
1,58 |
1,14 |
11,94013509 |
1,45 |
1,58 |
13,24985363 |
1,24 |
1,45 |
11,75527652 |
1,35 |
1,24 |
11,34400492 |
1,68 |
1,35 |
13,28776176 |
1,65 |
1,68 |
14,57102193 |
1,56 |
1,65 |
14,04090643 |
1,5 |
1,56 |
13,386915 |
Долгосрочный мультипликатор:
В
долгосрочном периоде при изменении
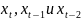на одну единицу
изменится на 10,8616.
xt |
xt-1 |
xt-2 |
yt |
1,45 |
1,78 |
1,23 |
16,70251 |
1,48 |
1,45 |
1,78 |
16,5791 |
1,12 |
1,48 |
1,45 |
14,40683 |
1,34 |
1,12 |
1,48 |
13,90519 |
1,38 |
1,34 |
1,12 |
14,26905 |
1,45 |
1,38 |
1,34 |
15,21687 |
1,14 |
1,45 |
1,38 |
14,21957 |
1,58 |
1,14 |
1,45 |
14,99793 |
1,45 |
1,58 |
1,14 |
15,65391 |
1,24 |
1,45 |
1,58 |
15,08722 |
1,35 |
1,24 |
1,45 |
14,4018 |
1,68 |
1,35 |
1,24 |
15,9027 |
1,65 |
1,68 |
1,35 |
17,41793 |
1,56 |
1,65 |
1,68 |
17,58373 |
1,5 |
1,56 |
1,65 |
16,86647 |
Вывод:
Я освоил методику построения модели с распределенным лагом, оценки ее параметров методом замены переменных, методом Алмона и анализ влияния факторов на выходную переменную.
В
данной модели лаговые переменные
оказывают влияние на значение
результативного признака, но с увеличением
лага их влияние падает. Более или менее
существенное влияние оказывают лаговые
переменные
.
В результате построения модели и проверки
ее коэффициентов получили функцию с
распределенным лагом:
,
но не все коэффициенты оказались
значимыми, в следствии чего их пришлось
убрать из модели.
Влияние капиталовложений в рекламу в краткосрочном периоде: при увеличении на 1 миллион руб. затрат на рекламу, объемы продаж вырастут на 4,458 млн. руб. Влияние капиталовложений в рекламу в среднесрочном периоде: при увеличении на 1 миллион руб. затрат на рекламу, объемы продаж вырастут на 8,7528 млн. руб. Капиталовложений в рекламу в долгосрочном периоде оказывают не столь значительное влияние: при увеличении на 1 миллион руб. затрат на рекламу, объемы продаж вырастут на 10,8616 млн. руб., то есть на 2,1088 млн. руб. увеличатся продажи в долгосрочном периоде по сравнению с краткосрочным.
Данную модель можно использовать для прогнозирования дальнейшего влияния капиталовложений в рекламу на объемы продаж продукции.