9.5. Простейшая одноканальная смо с неограниченной очередью

На одноканальную СМО (например, ЭВМ) поступает простейший поток заявок с интенсивностью . Время обслуживания заявок - показательное с параметром.

Рис. .4.

Длина очереди не ограничена. Граф состояний системы приведен на рис. 9.4:

s₀- единственный канал системы свободен;

s₁- канал занят, очереди нет;

s₂ - канал занят, одна заявка стоит в очереди;

s_i- канал занят,i-1 заявок ожидают своей очереди.

Снова имеем дело со схемой гибели и размножения. Финальные вероятности, если они существуют, даются формулами (7.6):

где  = /.

Рассмотрим ряд 1, ,₂,...,i,... Это частный случай ряда, составленного из членов геометрической прогрессии. Общий член такого ряда имеет вид

a_i= a _i-1 q = a₀q_i,

где q - знаменатель прогрессии. Суммаnчленов ряда равна

При nсуммаS_nостается конечной (ряд сходится) только при знаменателеq< 1. Сумма членов ряда стремится к пределу

(9.1)

Для анализируемой СМО знаменатель q = , а начальный член рядаa₀=1. Следовательно, стационарный режим возможен только при< 1, иначе очередь вырастает до бесконечности. Финальные вероятности в стационарном режиме равны

Определим показатели эффективности СМО.

Вероятность отказа в обслуживании P_отк=0.

Относительная и абсолютная пропускные способности Q=1;A=.

Среднее число заявок в системе

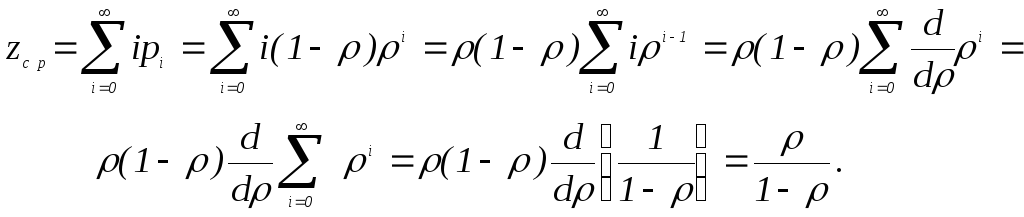
Здесь снова использовано условие < 1 и формула (9.1).

Среднее число занятых каналов

Средняя длина очереди

Среднее время пребывания в системе (по формуле Литтла)

Среднее время ожидания в очереди

Продолжим числовой пример п.9.3. При = 0.9 средняя длина очереди составитl_ср= 8.1, а при=0.5l_ср= 0.5.

9.6. Простейшая многоканальная смо с неограниченной очередью

Граф состояний такой системы изображен на рис. 9.5. Состояния системы перенумерованы по числу заявок в системе

s₀- СМО свободна;

s₁- занят один канал;

s_i- занято i каналов,i=1,2,...,k;

Рис. 9.5.

s_k- заняты всеkканалов, очереди нет;

s_k+j- заняты всеkканалов иjзаявок находятся в очереди.

На вход СМО поступает простейший поток заявок с интенсивностью . Время обслуживания одной заявки - показательное с параметром. Суммарная производительностьkканалов -k.

По формуле (7.6) находим вероятность состояния s₀:

где =/.

Рассмотрим ряд, образованный слагаемыми, заключенными в круглые скобки. При =/k< 1сумма членов ряда по формуле (9.1) при kстремящемся к бесконечности равна/ (1-). Условие< 1 необходимо для существования стационарного режима СМО. Следовательно,

Так как очередь не ограничена P_отк=0,Q=1,A=.

Среднее число занятых каналов k_ср=A/.

Средняя длина очереди

Среднее время ожидания в очереди находится по формуле Литтла ср=lср/.

9.7. Простейшая многоканальная смо с ограничением длины очереди

Сохраним условия и нумерацию состояний СМО такимиже как в предыдущей параграфе с той лишь разницей, что число мест в очереди ограничено числом m. Финальные вероятности состояний системы существуют при любом соотношении междуи.

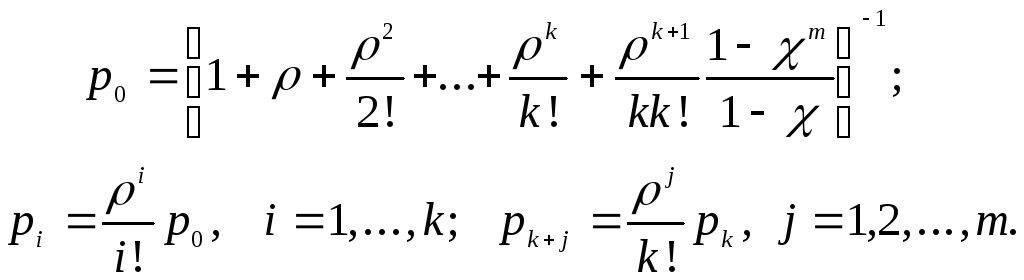
Здесь, как и раньше = /,= /k.

Характеристики эффективности СМО:

9.8. Простейшая многоканальная смо с “нетерпеливыми” заявками

Рассматривается k-канальная СМО (например, батарея ПВО сkпусковыми установками) [7]. Интенсивность потока заявок (среднее число самолетов противника в единицу времени) -. Продолжительность обслуживания имеет экспоненциальный закон с параметром.Число мест в очереди не ограничено, но ограничено время пребывания заявки в очереди некоторым случайным сроком T (время пребывания самолета в зоне пуска ракет ПВО). Это время также распределено экспоненциально с параметром. Иначе, на каждую заявку, стоящую в очереди, действует “поток уходов” с интенсивностью.

Рис. 9.6.

Граф состояний СМО изображен на рис. 9.6. Из него следует, что финальные вероятности состояний системы равны

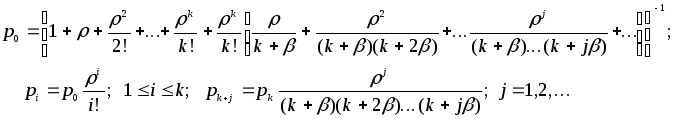
Здесь =/;=/.

Определим показатели эффективности СМО.

Интенсивность потока уходов, приходящаяся на одну заявку, равна . Следовательно, в единицу времени из очереди уходитl_срзаявок. Поэтому абсолютная пропускная способность СМО

A=-l_ср,

а относительная пропускная способность

Q=A/= 1-l_ср/.

Среднее число занятых каналов найдем из отношения абсолютной пропускной способности и “производительности” одного канала

k_ср=A/= -  l_ср.

Среднее число занятых каналов можно определить также как математическое ожидание числа занятых каналов

Поэтому средняя длина очереди l_ср= ( -k_ср) /.

Средние времена пребывания заявок на обслуживании и в очереди находятся по формуле Литтла.

Усложним несколько условия задачи. Пусть обслуживание производится с ошибками, без гарантии качества. С вероятностью p оно удовлетворяет заявку, а с вероятностью q = 1 - p - не удовлетворяет. Если плохо обслуженная заявка не обращается в СМО вторично, то все приведенные формулы остаются справедливыми. Реальная же пропускная способность системы, учитывающая лишь удовлетворенные заявки, составит A*=pA.

Если плохо обслуженные заявки обращаются в СМО повторно, то должна быть скорректирована интенсивность потока заявок - *=(1+q).