2.3.3. Смо с конечной очередью

СМО с конечной очередью длины т характеризуется тем, что при поступлении очередной заявки возможны три исхода:

– заявка немедленно принимается на обслуживание, если в си­стеме в данный момент находится k заявок и k<n;

– заявка становится в очередь, если п  k<n+m;

– заявка получает отказ и покидает систему, если k=n+m. Следовательно, в любой момент времени система может нахо­диться в одном из п+т+1 состояний, то есть множество состояний

Увеличение числа заявок в системе происходит только под воз­действием потока заявок интенсивности , а уменьшение числа зая­вок в системе — только в результате завершения обслуживания одной из заявок, то есть

(k занятых приборов порождают поток обслуженных заявок ин­тенсивности k ).

Р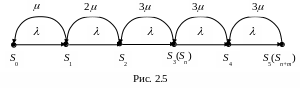 азмеченный граф состояний СМО с конечной очередью для п=3, т=2 изображен на рис. 2.5.

Для определения вероятностей состояний системы в формулы (2.16) и (2.17) подставим значения

и получим:

• для kn ;

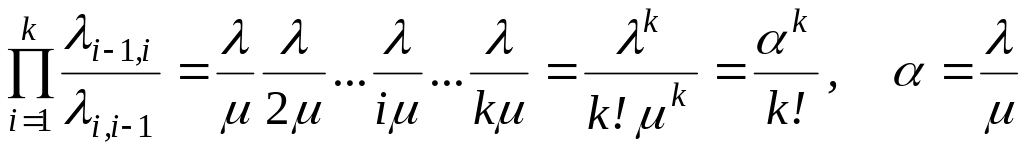• для k<n .

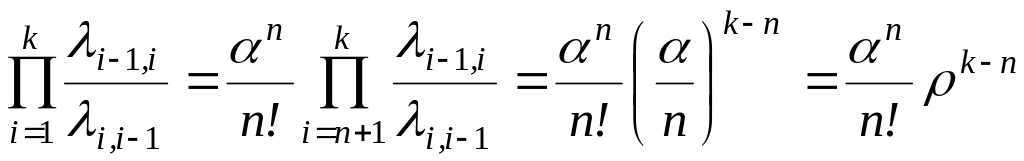Полагая в уравнении (2.17) N=n+m, находим

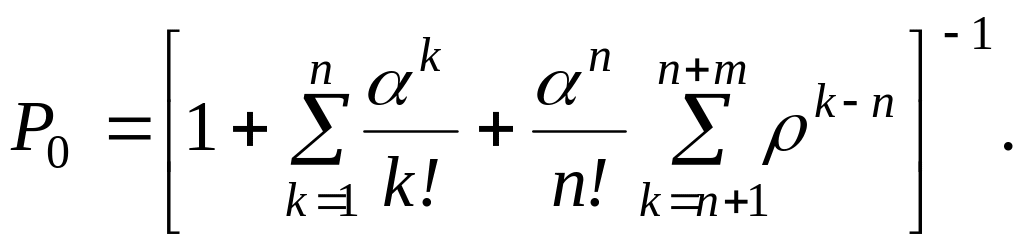(2.25)

Учитывая, что ⁰/0!=1 и вычисляя сумму т членов геометри­ческой прогрессии со знаменателем , находим

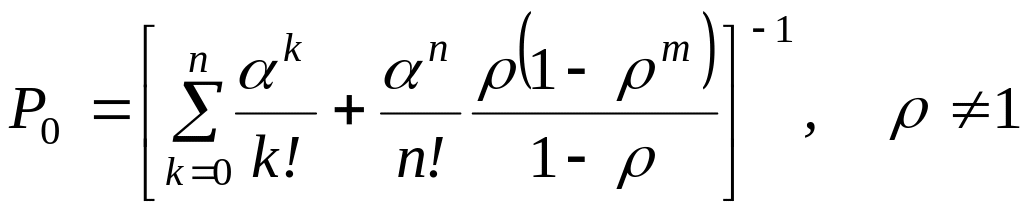(2.26)

Из уравнения (2.16) находим вероятности состояний

; (2.27)

(2.28)

На основании формул (2.25) – (2.28) определим основные по­казатели эффективности системы.

1. Вероятность отказа в обслуживании – это вероятность того, что в СМО имеется п+т заявок, то есть

(2.29)

Зная Р_отк по формулам (2.19) – (2.21), можно вычислить аб­солютную и относительную пропускную способность системы, сред­нее число занятых приборов, коэффициенты их загрузки и простоя.

2. Вероятность того, что поступившая в систему заявка заста­нет все каналы занятыми (не будет немедленно принята на об­служивание),

. (2.30)

3. Средняя длина очереди

,

где P_n+r – вероятность того, что в очереди находится ровно r зая­вок (k=n+r).

Подставляя в полученное выражение P_n+r, находим

; (2.31)

. (2.32)

4. Среднее время ожидания в очереди определяется как мате­матическое ожидание. Если к моменту поступления заявки в оче­реди находится r=0, 1, . . ., т–1 заявок, то она поступит на об­служивание после завершения обслуживания r+1 заявок, то есть

;

. (2.33)

Среднее время ожидания – это среднее время на­копления очереди длиной L.

Среднее число заявок, находящихся в СМО, и среднее время пребывания заявки в системе определяются по формулам (2.22) и (2.23) с учетом формул (2.31) – (2.33).

Из полученных соотношений следует, что показатели Р_отк, q, N_з, L, Y не зависят от конкретных значений  и , а только от их соотношения . Показатели напротив, чувствительны к изменению не только параметра , но и к изменению  при =const. Так, например, при увеличении  и  в два раза Р_отк, q, n_з и L не изменяются, Q увеличивается, а уменьшается в два раза, то есть при одновременном увеличении плотности потоков зая­вок и обслуживании характеристики процесса обслуживания улуч­шаются.

2.3.4. Смо с отказами

СМО с отказами является частным случаем СМО с конечной очередью при m=0. Полагая в формулах (2.25) – (2.29) т=0, найдем показатели эффективности СМО с отказами:

– вероятность простоя всех обслуживающих приборов из вы­ражения (2.26)

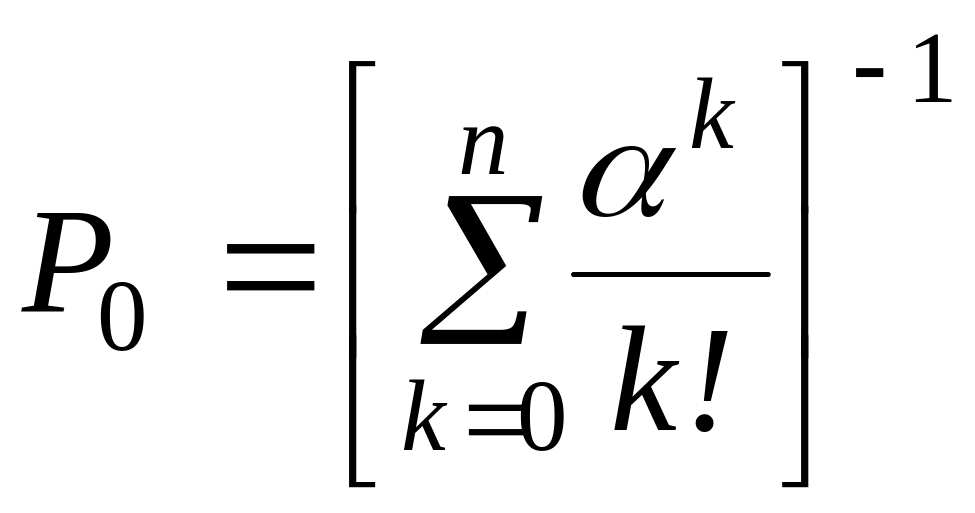; (2.34)

– вероятность того, что в системе находится k заявок, из фор­мулы (2.27)

; (2.35)

– вероятность отказа в обслуживании из выражения (2.29)

; (2.36)

– абсолютная и относительная пропускная способность систе­мы и среднее число занятых приборов

(2.37)

Зависимости (2.34) – (2.36) были впервые получены датским инженером А.К.Эрлангом и поэтому известны как формулы Эрланга.

Советский ученый Б.А.Севастьянов доказал, что формулы Эрланга справедливы при любом законе распределения времени об­служивания, но при конечном и постоянном значении его матема­тического ожидания. Это позволяет использовать соотношения (2.34) – (2.37) для решения широкого класса практических задач.