
- •Б7. Потенциал силы тяжести и его высшие производные. Нормальные значения вторых производных. Потенциал силы тяжести.
- •1.1.3. Производные потенциала силы тяжести.
- •Измеряемые в гравиразведке параметры.
- •2.1.2. Динамические методы.
- •Б9. Нормальное гравитационное поле Земли и его формулы. Нормальное значение силы тяжести.
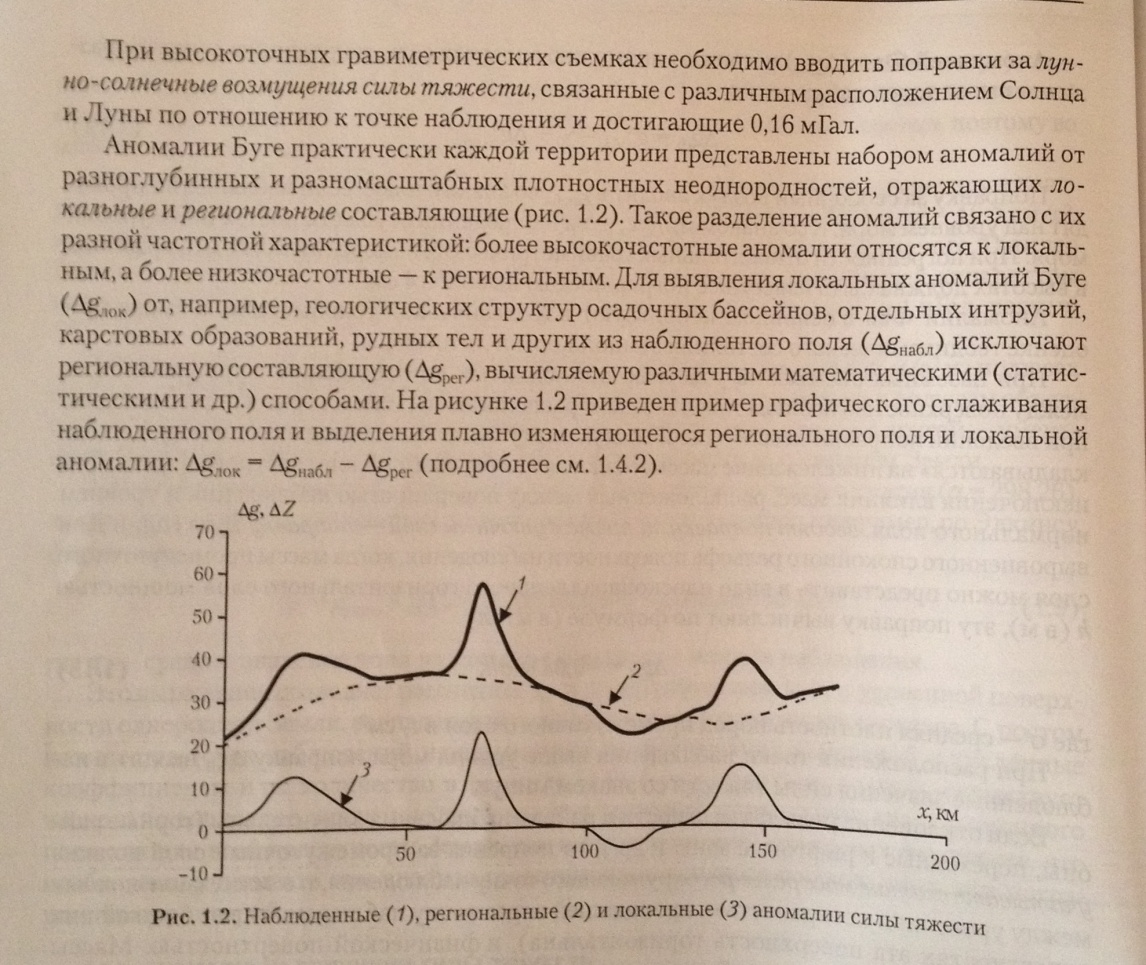
- •Редукции силы тяжести.
- •1.2.3. Аномалии силы тяжести.
- •4.1.2. Единицы измерений.
- •4.1.3. О происхождении магнитного поля Земли.
- •Нормальное геомагнитное поле.
- •4.1.5. Аномальные геомагнитные поля.
- •4.1.6. Вариации земного магнетизма.
- •Намагниченность горных пород и руд.
- •4.2.2. Магнитная восприимчивость горных пород и руд.
- •Остаточная намагниченность пород и руд.
- •5.1.2. Оптико-механические магнитометры.
- •5.1.3. Феррозондовые магнитометры.
- •5.1.4. Ядерно-прецессионные (протонные) магнитометры.
- •6.1. Качественная интерпретация данных магниторазведки.
- •6. 2. Количественная интерпретация данных магниторазведки.
- •20. Электрические св-ва горных пород.
- •21. Аппаратура для разведки постоянным током.
- •25. Палеточные способы интерпретации трехслойных кривых зондирований.
- •Метод РадиоКип
- •Дипольное электромагнитное профилирование (дэмп)
- •Дистанционные индукционные зондирования (диз)
1. Методика гравиметрической съемки. Обработка рейсов.



2+3. Теория гравиметров. Устройство и инструментальные испытания. Теория и принцип устройства гравитационного вариометра и градиентометра.



4. Редукции (поправки за высоту, за притяжение промежуточного слоя, за рельеф местности, изостатические).

5. Решение простых задач гравиразведки для простых тел: призма, параллелепипед, горизонтальная пластинка.
6. Решение простых задач гравиразведки для простых тел: вертикальных стержень, уступ, конечная горизонтальная линия.
Б7. Потенциал силы тяжести и его высшие производные. Нормальные значения вторых производных. Потенциал силы тяжести.
Потенциал
силы тяжести (![]() )
был введен в теорию гравиметрии для
облегчения решения теоретических задач.
В точке А, расположенной на расстоянии rA от
центра Земли, выражение для потенциала
принимается равным: WA=GM/rA,
а в любой точке B, расположенной на
продолжении радиуса
)
был введен в теорию гравиметрии для
облегчения решения теоретических задач.
В точке А, расположенной на расстоянии rA от
центра Земли, выражение для потенциала
принимается равным: WA=GM/rA,
а в любой точке B, расположенной на
продолжении радиуса ![]() ,
, ![]() .
Поэтому разность потенциалов будет
равна:
.
Поэтому разность потенциалов будет
равна:
|
В
пределе при малом ![]() имеем:
имеем:
|
отсюда g=-dW/dr, т.е. сила тяжести есть производная потенциала силы тяжести по направлению к центру Земли.
С
другой стороны, работа, которая может
быть произведена при движении притягиваемой
точки по отрезку
,
равна ![]() .
Поэтому
.
Поэтому ![]() ,
или работа силы тяжести по перемещению
единичной массы на отрезке
равна
разности значений потенциала на концах
этого отрезка.
,
или работа силы тяжести по перемещению
единичной массы на отрезке
равна
разности значений потенциала на концах
этого отрезка.
При перемещении точки в направлении, перпендикулярном силе тяжести, dW=0. Это означает, что W=const. Поэтому гравитационное поле можно представить в виде набора бесконечного числа поверхностей, на которых потенциал остается постоянным, а ускорение силы тяжести направлено перпендикулярно этой поверхности. Такие поверхности называют эквипотенциальными или уровенными. В частности, поверхность жидкости на Земле, например, моря, совпадает с уровенной поверхностью. У Земли есть одна уникальная уровенная поверхность, которая совпадает с невозмущенной волнениями поверхностью океанов. Она называется геоидом.
Таким образом, геоид - это условная уровенная поверхность, которая совпадает со средним уровнем океанов и открытых морей, проходит под сушей и по определению везде горизонтальна, а ускорение силы тяжести к ней перпендикулярно.
1.1.3. Производные потенциала силы тяжести.
Производные
потенциала силы тяжести по трем
координатным осям ![]() ,
, ![]() ,
, ![]() однозначно
определяют его полный вектор.
однозначно
определяют его полный вектор.
В
частности, если ось z направить
к центру Земли, то ![]() ,
а
,
а ![]()
В гравиметрии кроме первых производных изучаются вторые производные потенциала или их разности:
|
(1.3) |
Физический
смысл этих выражений легко получить,
если иметь в виду, что ![]() .
Так, например, вторая производная
.
Так, например, вторая производная ![]() указывает
на скорость изменения силы тяжести по
оси х,
т.е. является горизонтальным градиентом
силы тяжести.
указывает
на скорость изменения силы тяжести по
оси х,
т.е. является горизонтальным градиентом
силы тяжести.
Аналогичный
смысл имеют вторые производные ![]() и
и ![]() .
.
Вторые
производные ![]() ,
, ![]() характеризуют
форму уровенной поверхности (геоида),
изучаемую в геодезической гравиметрии.
Практической единицей измерения
градиента силы тяжести принимается 1
этвеш (Е)=10-9/c2,
что соответствует изменению силы тяжести
в 0,1 мГал на 1 км.
характеризуют
форму уровенной поверхности (геоида),
изучаемую в геодезической гравиметрии.
Практической единицей измерения
градиента силы тяжести принимается 1
этвеш (Е)=10-9/c2,
что соответствует изменению силы тяжести
в 0,1 мГал на 1 км.
Б8. Законы колебания математического и физического маятника. Относительные определения силы тяжести.
Измеряемые в гравиразведке параметры.
Основным
измеряемым параметром в гравиразведке
является ускорение силы тяжести ![]() ,
которое определяется либо абсолютно,
либо относительно. При абсолютных
измерениях получают полное (наблюденное)
значение ускорения
,
которое определяется либо абсолютно,
либо относительно. При абсолютных
измерениях получают полное (наблюденное)
значение ускорения ![]() ,
при относительных - его приращение
относительно некоторой исходной точки
,
при относительных - его приращение
относительно некоторой исходной точки ![]()
Методы измерения ускорения силы тяжести и его приращения делятся на динамические и статические. Под динамическими понимаются такие методы, в которых наблюдается движение тела под действием силы тяжести (качание маятника, свободное падение тел и др.) В этом случае g определяется через параметры движения тела и параметры установки. В статических методах действие силы тяжести компенси\-руется (например, силой упругости пружины), а g определяется по изменению статического положения равновесия тела.
Реже
в гравиразведке измеряются вторые
производные гравитаци\-онного потенциала ![]()
