
Химическое равновесие
Химические реакции протекают в двух направлениях: прямая (→) и обратная (←). Рано или поздно скорости этих реакций сравниваются, так как скорость прямой реакции уменьшается, а скорость обратной реакции увеличивается, и наступает состояние химического равновесия. Химическая термодинамика позволяет рассчитать, при каком давлении (P) и при какой температуре (Т) наступает равновесие, рассчитать состав равновесной смеси.
Уравнение изотермы химических реакций – основное уравнение термодинамики
По этому уравнению, в зависимости от величины и знака перед ∆G судят о направлении процесса или его равновесии.
Возьмём условную реакцию:
n1A + n2B ↔ n3C + n4D
Р и Т = const, А, B – исходные вещества, C, D – конечные продукты, n1, n2, n3, n4 –стехиометрические коэффициенты.
Изменение энергии Гиббса, как функции состояния, можно выразить как разность конечных и начальных величин: ∆G = Gкон – Gнач
Для реакции в целом: ∆G = ∑nкGкон – ∑nнGнач.
∆G = (n3GC+ n4GD) – (n1GA + n2GB)
Подставим Gi = Gi0 + RTlnai и приведём к виду:
∆GT
= ∆GT0
+ RTln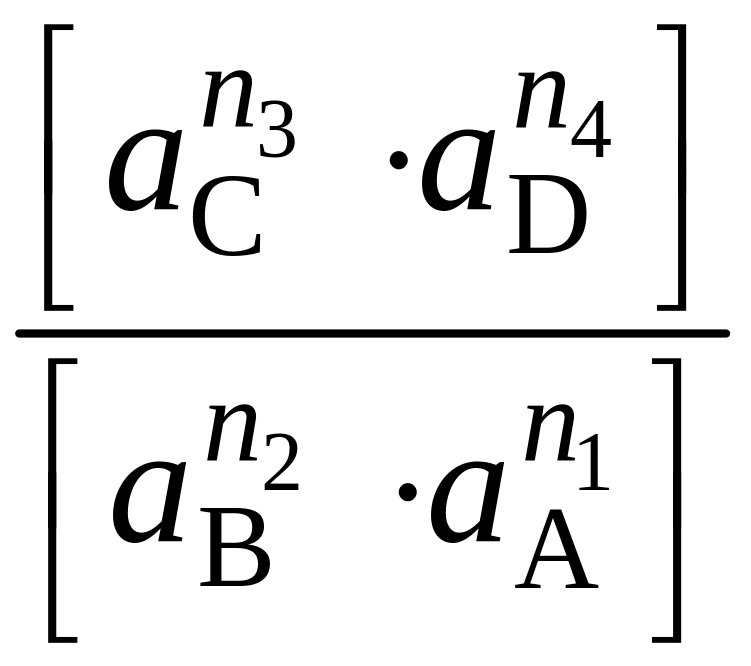 ;
где
∆GT0
= (n3GC0+
n4GD0)
– (n1GA0
+ n2GB0)
∆GT0
– стандартное
изменение энергии Гиббса при любой T.
;
где
∆GT0
= (n3GC0+
n4GD0)
– (n1GA0
+ n2GB0)
∆GT0
– стандартное
изменение энергии Гиббса при любой T.
Для него: aA = aB = aC = aD = 1
Если ∆GT < 0, то реакция протекает в прямом направлении, если ∆GT > 0,то реакция протекает в обратном направлении, если ∆GT = 0, то система находится в равновесии.
Примечание: реакция условно считается находящейся в равновесии, если ∆GT0 лежит в интервале ±10 кДж/моль.
Рассмотрим уравнение изотермы для состояния равновесия:
∆GT = 0
∆GT0 = –RTln ;
В отличие от общего вида уравнения изотермы, здесь под логарифмом – отношение активностей при равновесии.
Это равновесное соотношение активностей называется константой равновесия:
Ка = или ∆GT0 = –RTlnКа.
Оба эти выражения справедливы для неидеальной газовой или конденсированной систем.
В области низких давлений Р ≤ 1атм, ai ≈ Рi:
∆GT
= ∆GT0
+ RTln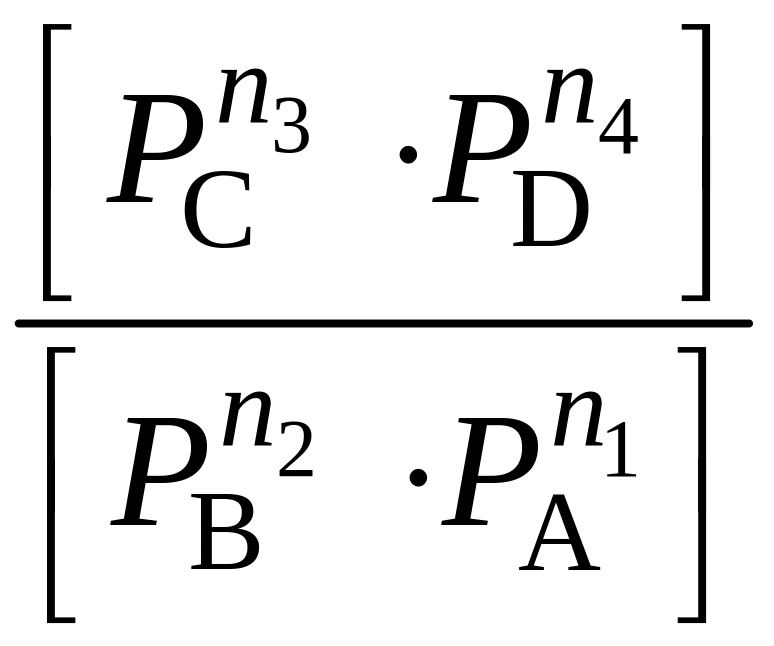 ,
,
где PA, PB, PC, PD – парциальные давления компонентов.
Кр = или ∆GT0 = –RTlnКр
Аналогично в области низкихконцентраций газа:
∆GT
= ∆GT0
+ RTln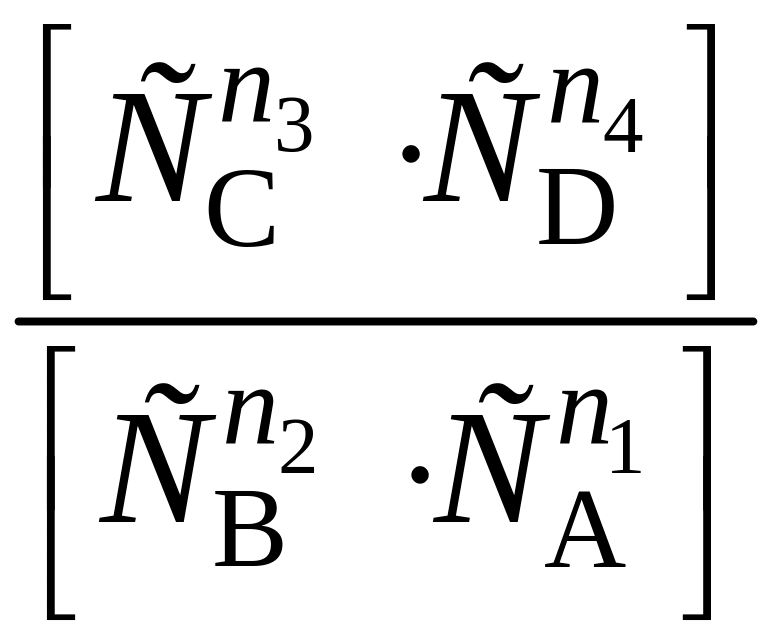 ,
,
Кc = или ∆GT0 = –RTlnКc
Примечание: при V = const уравнение изотермы выражают аналогично предыдущему выражению, но через ∆F.
Закон действующих масс:
Для каждой данной температуры отношение произведения равновесных активностей (Pi, Ci, Ni) конечных продуктов к произведению активностей (Pi, Ci, Ni) начальных продуктов в степенях соответствующих их стехиометрическим коэффициентам есть величина постоянная, называемая константой равновесия.
Соотношения между константами равновесия
1. Кр и Кс
Кр =
Уравнение состояния через парциальное давление:
PiV = niRT ;
Pi
=
![]() ∙RT
= СiRT;
∙RT
= СiRT;
Кр = RTn;
Кр =KcRTn;
∆n = (n3 + n4) – (n1 + n2);
Если ∆n = 0, то Кр = Кс;
Примечание: Расчет Кр в Па.
∆G = ∆G0 + RTln ;
Если PA = PB = PC = PD, то
∆G = ∆G0 + RTlnP∆n;
Если Р = 1 атм., то
∆G = ∆G0 + RTln Кр;
Если Р = 101325 Па, то
∆G = –RTln Кр + ∆nRT (11,53);
2. Кр и КN
Кр = ;
Используем следствие закона Дальтона
Pi = NiP, где Ni – мольная доля.
Кр
= ;
;![]()
Кр
= KN![]() ;
;
∆n = (n3 + n4) – (n1 + n2);
При расчете ∆n жидкие и твёрдые фазы не учитываются.
