27. Вычет. Теор. О вычетах.

опр. а - изол. особ. f(z). Вычетом ф-ции в т. а наз. число, равное 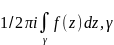- некот. окр., целиком лежащая в проколот. окр. т. а, не содержащей других особ. точек ф-ции f(z). Обозн. .

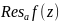теор. 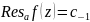(вычет равен коэфф. при -1 степени в ее разлож. в ряд Лорана в окр. т. а).

а - ноль порядка m. 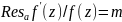. а - полюс порялка k. .

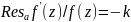теор. о вычетах: пусть ф-ция f(z) аналит.в обл. D за искл. конечного числа особ. т. a_k r=1,…,n. И пусть контур Г целиком лежит в обл. D и не проходит ни через одну из особ. точек ф-ции f(z), причем все особ. т. лежат внутри этого контура. Тогда .

док-во: (пицца) поведем n окр. |z-a_k|=r_k так чтобы они целиком лежали внутри контура Г так, что бы внутри каждой из этих окр. сод. токльо одна особ. т. ф-ции и не они не имели общих точек - γ_k. ч.т.д.

28. Логарифмический вычет. Принцип аргумента.

опр. Логарифм. вычетом ф-ции f(z) в точке а наз. вычет ее логарифм. произв. .

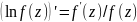теор. f(z) аналит. в обл. D, за искл. конечного числа полюсов 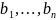кратностей 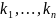соотв., и имеет в этой обл. нули 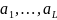кратностей 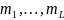. Пусть контур Г целиком лежит в обл. D и охватывает все полюсы и нули ф-ции f(z). Тогда справедливо равенство 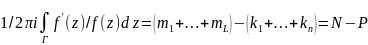. (Кол-во нулей - кол-во полюсов). док-во:

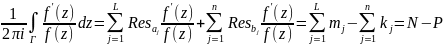
теор. Пусть f(z) аналит. в обл. D за искл. конечного числа полюсов кратностей , и обращается в в ноль в т. кратностей 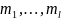(эль малое). Пусть кривая L целиком лежит в обл. D и охватывает все нули и полюсы ф-ции. Тогда разность между числом нулей и числом полюсов равна деленному на 2π изменению аргумента ф-ции f(z) при обходе кривой L. .

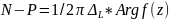29.Теорема Руше.

Пусть ф-ции f(z) и ф(z) аналит. в обл. D и контур L целиком лежит в этой обл. тогда если на контуре вып. нер-во 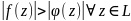, то ф-ция f(z) и ф-ция f(z)+ф(z) имеют внутри контура L одинаковое число нулей.

док-во: т.к. 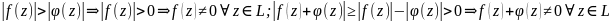Применим к ф-ции f(z)+ф(z) принцип аргумента: 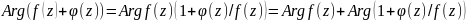. Рассм. последнее слагаемое: 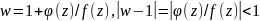. Значит знач. ф-ции w лежат внутри круга радиуса 1 с ц. в т. 1. Изменение вдоль контура L 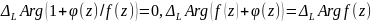т.к. f(z) и ф(z) тоже аналит. в D, а знач. не имеет полюсов, т.о. в силу принципа аргумента 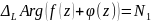, где N₁ - число нулей ф-ции внутри L. 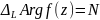, где N - число нулей ф-ции внутри L. => N₁=N - число нулей этих ф-ций совпадают, ч.т.д.

30. Основная теорема алгебры.

Любой многочлен степени n 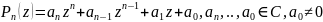, имеет ровно n корней с учетом их кратностей.

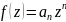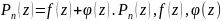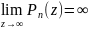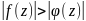док-во: Рассм. ф-цию и , тогда - аналит. в C. т.к. то сущ. такая окр. L: |z|=R, что все корни многочлена лежат внутри этой окр., а на самой окр. вып. нер-во , тогда в силу теор. Рушк ф-ции f(z) и P_n(z) имеют внутри L одинаковое кол-во нулей => P_n(z) имеет n корней (нулей), ч.т.д.