
23. Ряд Лорана. Теор. Лорана.
Ряд Лорана примен. для представления аналит. ф-ций в круге. Явл. обощением ряда Тейлора и позв. исслед. ф-ции в кольцевых обл. z<|z-a|<R.
Теор. Лорана: Всякую ф-цию f(z) аналит. в кольце z<|z-a|<R можно представить в виде суммы сход. ряда:

док-во:
обозн. кольцо,
в кот. аналит. ф-ция через К. Рассм. произв.
т. zК.
Построим кольцо К’, целиком леж в К, так
чтобы zK’
Обозн границу этого кольца через Г1
и Г2.
Получим, что ф-ция f(z)
аналит. в K’
и на его границе. Тогда для этого кольца
K’
справедлива фор-ла Коши:
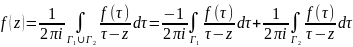 .
Рассм. их по отдельности: по Г2:
Разложим ф-цию
.
Рассм. их по отдельности: по Г2:
Разложим ф-цию
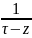 по степеням (z-a):
по степеням (z-a):
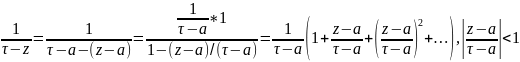 .
На окр. Г2
получ. степ. ряд будет сх-ся равномерно,
а f(z)
- аналит. на Г2,
знач. явл. огранич., значит ряд
.
На окр. Г2
получ. степ. ряд будет сх-ся равномерно,
а f(z)
- аналит. на Г2,
знач. явл. огранич., значит ряд
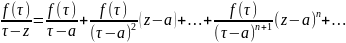 сх-ся равн. значит его можно проинтегр.
по окр. Г2:
сх-ся равн. значит его можно проинтегр.
по окр. Г2:
 .
по Г1:
Рассм. ф-цию
и разл. ее по степеням
.
по Г1:
Рассм. ф-цию
и разл. ее по степеням
 :
:
 - геометрич. прогрессия. Данный ряд сх-ся
равн. на окр. Г1
и ф-ция f(z)огран.
на этйо окр., тогда ряд
- геометрич. прогрессия. Данный ряд сх-ся
равн. на окр. Г1
и ф-ция f(z)огран.
на этйо окр., тогда ряд
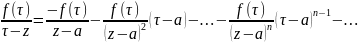 равн. сх-ся на Г1,
значит его можно почленно интегр.:
равн. сх-ся на Г1,
значит его можно почленно интегр.:
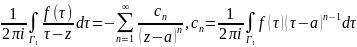 .
Проведем окр. γ
так, что бы она лежела между Г1
и Г2,
тогда по сл. из теор. Коши f(z)
можно предст. в виде:
.
Проведем окр. γ
так, что бы она лежела между Г1
и Г2,
тогда по сл. из теор. Коши f(z)
можно предст. в виде:
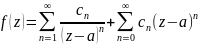 .
Первый ряд сх-ся во внешности окр. Г1,
второй - во внутренности окр. Г1,
тогда:
.
Первый ряд сх-ся во внешности окр. Г1,
второй - во внутренности окр. Г1,
тогда:
 ,
ч.т.д.
,
ч.т.д.
опр. ф-ный ряд (*) коэф. кот. нах-ся по фор-ле (**) наз. рядом Лорана ф-ции f(z) в кольце z<|z-a|<R.
опр. Сов-ть членов ряда Лорана с отриц. степенями наз. главной частью ряда,, а с положит. - правильной.
сл.: всякий сх-ся ряд по целым степеням (z-a) явл. рядом Лорана своей суммы.
24. Устранимые особые точки.
опр. т. а - наз. изолированной особенностью ф-ции если f(z) аналит. в некот. проколотой окр. т. а, а в самой т. а может быть и не аналит.
опр. т. а наз. устранимой особой т. f(z) если разложение в ряд Лорана не содержит членов с отриц. степенями, то есть главная часть = 0.
теор.
т. а явл. устранимой особ. ф-ции f(z)
т и т т, когда в этой т. сущ. конечный
предел
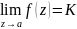 .
.
док-во:
1. необх: дано:
а -устр., док-ть:
сущ предел.
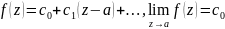 .
.
2. дост: дано: предел, док-ть: нет главной части. в ряде Лорана при устремлении za получим, что главная часть дает бесконечность, правильная - б/м величины, т.к. предел=число, то значит главная часть=0.
25. Полюсы ф-ции комп. перем.
опр. т. а - наз. изолированной особенностью ф-ции если f(z) аналит. в некот. проколотой окр. т. а, а в самой т. а может быть и не аналит.
опр. т. а наз полюсом f(z) если главная часть ее разложения в ряд Лорана в окр. т. а содержит конечное число членов. Наим. показатель степени наз. порядком полюса.
теор.
т. а явл. полюсом f(z)
т и т т, когда
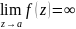 .
.
док-во:
1. необх: дано:
а-полюс, док-ть:
предел. Рассм. ф-цию
 -аналит.
в окр. т. а, тогда
-аналит.
в окр. т. а, тогда
 .
.
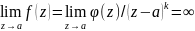 .
.
2.
дост. дано:
предел. док-ть:
а-полюс.
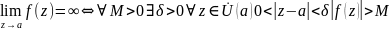 ,
значит вып. и для M=1,
значит в некот. окр. т. а f(z)0.
Рассм.
,
значит вып. и для M=1,
значит в некот. окр. т. а f(z)0.
Рассм.
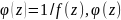 -аналит.
в некот. окр. т. а, более того
-аналит.
в некот. окр. т. а, более того
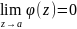 .
В силу аналит. фи(z)
в окр. т. а можно представить в виде степ.
ряда и т. а будет явл. устранимой
особенностью:
.
В силу аналит. фи(z)
в окр. т. а можно представить в виде степ.
ряда и т. а будет явл. устранимой
особенностью:
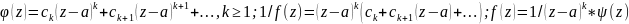 -
аналит. в окр. т. а.
-
аналит. в окр. т. а.
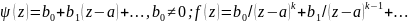 - конечное число отриц. степеней.
- конечное число отриц. степеней.
26. Сущ. особые точки. Теор. Сохоцкого-Вейерштрасса.
опр. т. а - наз. изолированной особенностью ф-ции если f(z) аналит. в некот. проколотой окр. т. а, а в самой т. а может быть и не аналит.
опр. т. а наз. суш. особой т. ф-ции f(z) если главная часть разлож. в ряд Лорана этой ф-ции в окр. т. ф содержит беск. много слагаемых.
теор.
т. а сущ. особой т. ф-ции f(z)
т и т т, когда в этой т. не сущ. предела
ф-ции
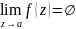 .
.
док-во: 1. необх: дано: ф-суш.особ. док-ть: предел не сущ. Предположим, что предел сущ. тогда возм. варианты: он либо конечен, либо беск. Если конечен - ф -устр. особ. => гл. часть не соделжить ни 1 члена. Если беск. - а-полюс => гл. часть сод. кон. число сленов. Противоречие - предел не сущ. 2.дост. дано: предел не суш. док-ть: а-сущ.особ. а не может быть устран. особ. ни полюсом. То есть гл. часть содержит счетное кол-во слагаемых, знач. а - сущ. особ.
теор.Сахотского-Вейерштрасса: если т. а сущ. особ. точка ф-ции f(z), то AC включая A=, zna, f(zn)A. (сущ. посл-ть zn сх. к а, такая что посл. f(zn) сх. к A).
