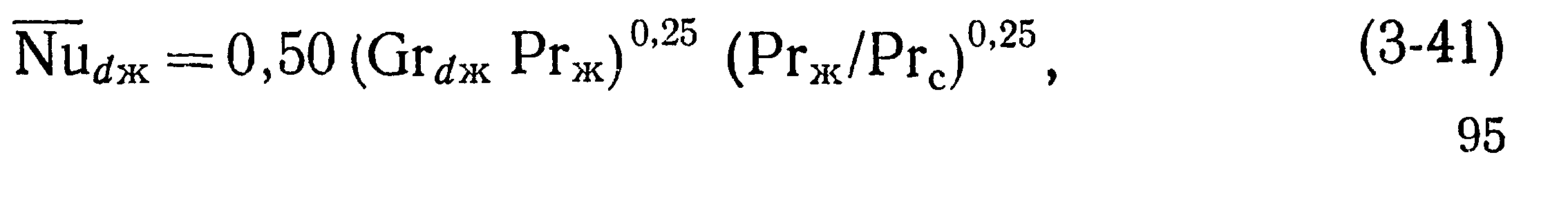15 Теплоотдача при поперечном обтекании вынужденным потоком и трубных пучков

Наиболее распростра­нены в технике два основных типа трубных пучков: коридорные рис.а и шахматные рис. Б шахматные рис. Б

В трубных пучках трубы первого ряда находятся приблизитель­но в тех же условиях, что и одиночный цилиндр. На теплообмене второго и последующих рядов сказывается турбулизация потока, создаваемая первыми рядами, но эффект добавочной турбулизации постепенно ослабевает по мере увеличения числа предшествующих поперечных рядов. Экспериментально установлено, что, начиная с третьего ряда, поток практически стабилизирован, поэтому и сред­ний коэффициент теплоотдачи для всех последующих рядов можно считать постоянной величиной.

Средний коэффициент теплоотдачи для третьего и последующих рядов труб может быть вычислен по следующему уравнению:

Ш_ж = CRe^Pr^³³ (Рг_ж/Рг_с)°'²⁵ 8,8_Ф,

■Где для шахматных пучков С=0,41; я=0,60; для коридорных пучков С=0,26; я=0,65. Поправочный коэффициент г₃ учитывает влияние относительных шагов: для шахматного пучка при Si/s₂<2 е₅= (V^)''*'. При S]/s₂>2 8^=1,12; для кори­дорного пучка e_s= (s₂/d)^-0'¹⁵

Средний для всего пучка коэффициент теплоотдачи можно вы­числить по формуле

ai^i + a₂F₂ + ... +a_nF_n

Fi+F,+ ...+F_n ■' где Fi, F₂, . . ., F_n — площадь поверхности труб соответствующего ряда

16 Характер, режимы движения и теплоотдачи при свободной коныекции в большом обьеме Теплоотдача в неограниченном пространстве. Процесс теплообмена при свободной конвекции (свободное движение) жидкости имеет весьма широкое распространение как в технике, так и в в быту. Свободным называется движение жидкости вследствие разности плотностей нагретых и холодных частиц. Например, при соприкосновении воздуха с нагретым телом воздух нагревается, становится легче и поднимается вверх. Если же тело холоднее воздуха, тогда, наоборот, от соприкосновения с ним воздух охлаждается, становится тяжелее и опускается вниз. В этих случаях движение воздуха возникает без внешнего возбуждения в результате самого процесса теплообмена. На рис. 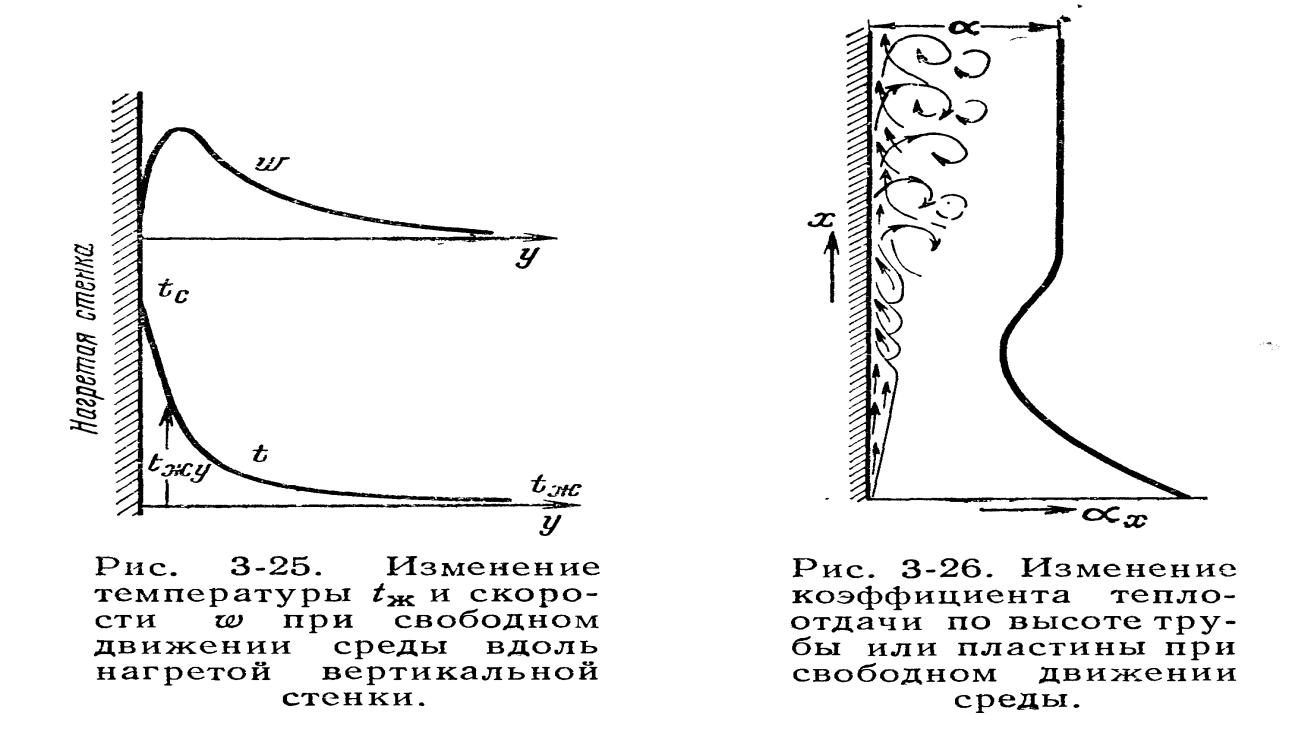3-24 показана типичная картина движения нагретого воздуха вдоль вертикальной трубы. При свободном движении жидкости в пограничном слое температура жидкости изменяется от tc до tж, а скорость — от нуля у стенки проходит через максимум и на большом удалении от стенки снова равна нулю (рис. 3-25). Вначале толщина нагретого слоя мала и течение жидкости имеет струйчатый, ламинарный характер. Но по направлению движения толщина слоя увеличивается и при определен ном ее значении тeчение жидкости становится неустойчивым, волновым, локонообразным и затем переходит в неупорядоченно-вихревое, турбулентное, с отрывом вихрей от стенки. С из- изменением характера движения изменяется и теплоотдача. При ламинарном движении вследствие увеличения толщины пограничного слоя коэффициент теплоотдачи по направлению движения убывает, а при турбулентном он резко возрастает и затем по высоте остается постоянным (рис. 3-26). В развитии свободного движения форма тела играет второстепенную роль. Здесь большее значение имеют протяженность поверхности, вдоль которой происходит движение, и ее положение. 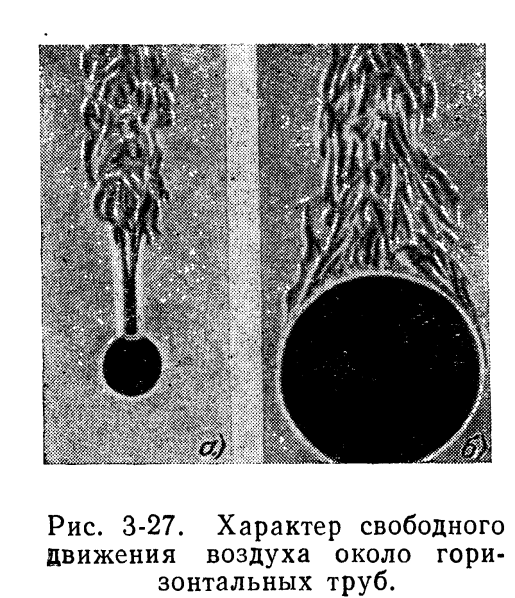Описанная выше картина движения жидкости вдоль вертикальной стенки (или вдоль вертикальной трубы) типична также и для горизонтальных труб и тел овальной формы. 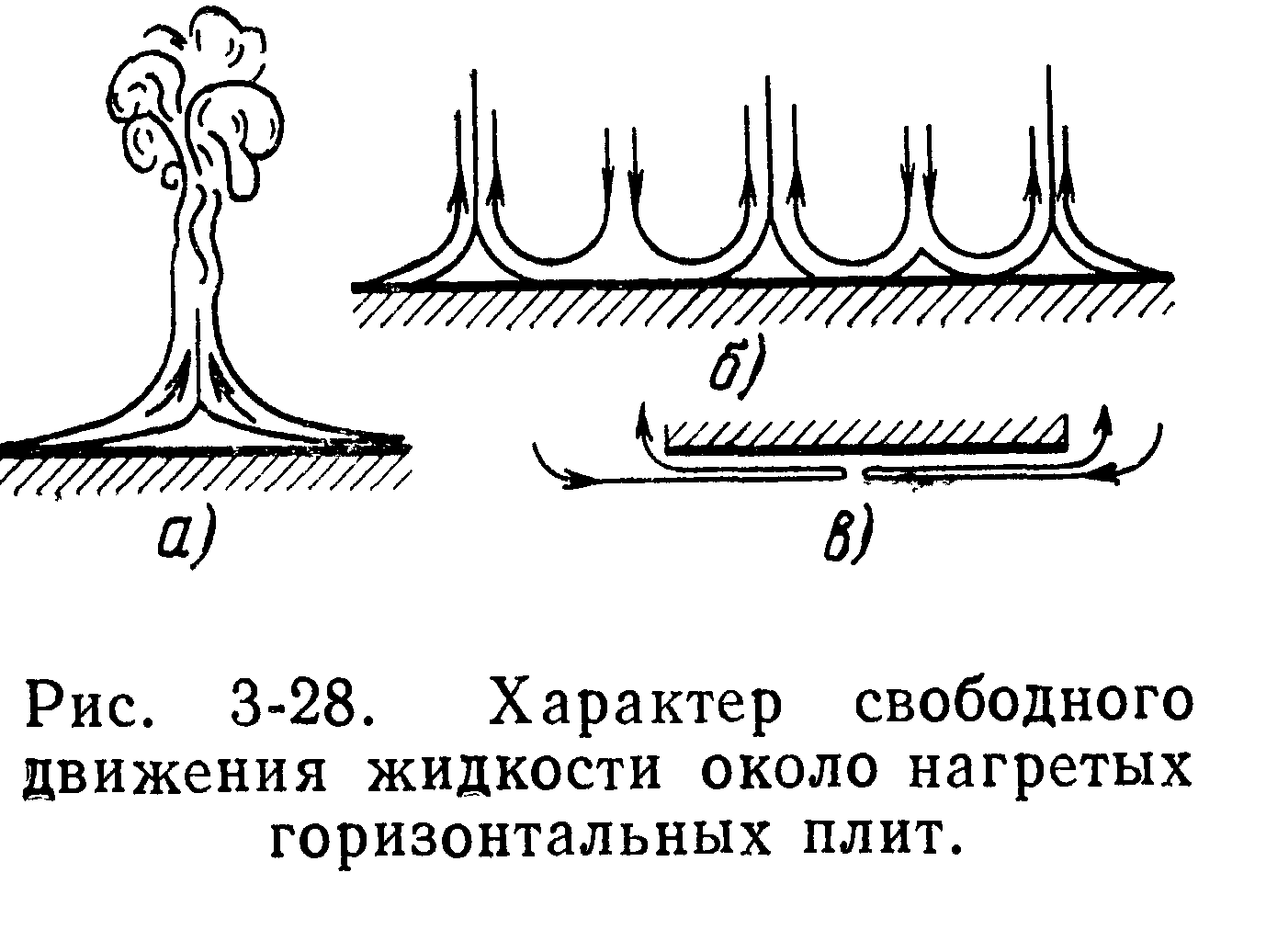Характер движения воздуха около нагретых горизонтальных труб различного диаметра представлен на рис. 3-27. Около нагретых горизонтальных плоских стенок или плит движение жидкости имеет иной характер и в значительной мере зависит от положения плиты и ее размеров. Если нагретая поверхность обращена кверху, то движение протекает по схеме рис. 3-28,а. При этом если плита имеет большие размеры, то вследствие наличия с краев сплошного потока нагретой жидкости центральная часть плиты оказывается изолированной. Ее вентиляция происходит лишь за счет притока (провала) холодной жидкости сверху (рис. 3-28, б). Если же нагретая поверхность обращена вниз, то в этом случае движение происходит лишь в тонком слое под поверхностью (рис. 3-28, в); остальная же масса жидкости ниже этого слоя остается неподвижной. По изучению интенсивности теплообмена в условиях свобод- свободного движения были проведены исследования с разными телами и различными жидкостями. В результате обобщения опытных данных получены уравнения подобия для средних значений коэффициента теплоотдачи. В этих формулах в качестве определяющей температуры принята температура окружающей среды tm. В качестве определяющего размера для горизонтальных труб принят диаметр d, а для вертикальных поверхностей — высота h. Закономерность средней теплоотдачи для горизонтальных труб диаметром d при (рис. 3-29) имеет вид